▷ ما هو وكيف يتم حساب الرقم التوافقي (أمثلة)

نشرح في هذه الصفحة ما هو الرقم التوافقي وكيف يتم حسابه (الصيغة). بالإضافة إلى ذلك، ستتمكن من رؤية أمثلة حول كيفية حساب أي رقم اندماجي والتدرب على التمارين التي تم حلها خطوة بخطوة. نعرض أيضًا جميع خصائص وتطبيقات الأعداد التوافقية. وأخيرًا، نتعلم كيفية إيجاد نتيجة عدد اندماجي مباشرة باستخدام الآلة الحاسبة.

ما هو الرقم التوافقي؟

في الرياضيات، الرقم التوافقي ، ويسمى أيضًا معامل ذو الحدين، هو عدد المجموعات العادية (مجموعات بدون تكرار) لمجموعات من عناصر k التي يمكن تشكيلها من مجموعة من عناصر n (n>k).

يتم التعبير عن الرقم التوافقي بين قوسين على النحو التالي:

$\begin{pmatrix}n \\ k \end{pmatrix}$

من ناحية أخرى، تتم قراءة الرقم التوافقي n على k . وبالمثل، يسمى n البسط ويسمى k الترتيب.

فقط مع تعريف الرقم التوافقي، من الصعب فهم معناه. ومع ذلك، سنرى الآن كيف يتم تحديد العدد التوافقي رياضيًا، وبعد ذلك سنتعمق أكثر في مفهوم التوافقيات هذا. سترى أنه بهذه الطريقة سوف تفهم الأمر بشكل أفضل.

صيغة العدد التوافقي

صيغة حساب قيمة الرقم التوافقي (أو معامل ذي الحدين) هي كما يلي:

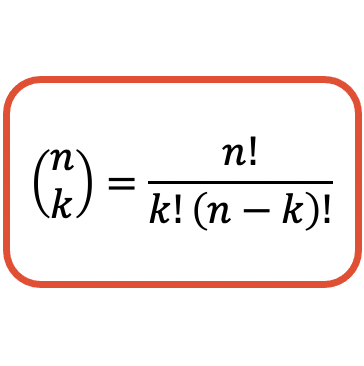
تذكر أن علامة التعجب في الجبر تتوافق مع مضروب الرقم. ولإيجاد مضروب رقم ما، عليك ضرب جميع الأعداد الصحيحة الموجبة للرقم 1 في هذا الرقم. على سبيل المثال، لحساب مضروب الرقم 4 يجب عليك ضرب 1 و 2 و 3 و 4:

$4! = 1\cdot 2 \cdot 3 \cdot 4 =24$

ومن المهم أيضًا أن تعرف أن مضروب 0 يساوي 1.

$0! = 1$

مثال لحساب رقم اندماجي

بعد ذلك، سوف نحدد قيمة الرقم الاندماجي خطوة بخطوة كمثال، حتى تتمكن من رؤية كيف يتم ذلك:

احسب قيمة العدد التوافقي 5 على 3.

معامل ذو الحدين 5 على 3 يتوافق مع التعبير التالي:

$\begin{pmatrix}5 \\ 3 \end{pmatrix}$

لذلك، إذا طبقنا صيغة الأعداد التوافقية، لتحديد قيمتها يجب علينا إجراء العمليات التالية:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!(5-3)!}$

أو ما يعادلها:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!\cdot 2!}$

لذلك نجد العوامل:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{1\cdot 2 \cdot 3 \cdot 4 \cdot 5}{(1\cdot 2 \cdot 3) \cdot (1\cdot 2)}$

يتم تكرار الضرب 1·2·3 في البسط والمقام، لذلك يمكن تبسيط الكسر عن طريق حذف هذا العامل:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{\cancel{1\cdot 2 \cdot 3} \cdot 4 \cdot 5}{(\cancel{1\cdot 2 \cdot 3)} \cdot (1\cdot 2)}$

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{ 4 \cdot 5}{1\cdot 2}$

الآن نحسب المنتجات:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{20}{2}$

وأخيرًا نقوم بالتقسيم:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \bm{10}$

خصائص العدد التوافقي

يمكن دمج الأعداد التوافقية، أو المعاملات ذات الحدين، وفقًا للخصائص التالية:

الرقمان التوافقيان التكميليان هما العددان اللذان لهما نفس البسط n ومجموع ترتيبهما يعادل البسط المذكور. وبالتالي، فإن نتيجة رقمين اندماجيين متكاملين متطابقة.

$\begin{pmatrix}n \\ k \end{pmatrix} = \begin{pmatrix}n \\ n-k \end{pmatrix}$

وتسمى هذه الخاصية للأعداد التوافقية أيضًا بهوية التناظر.

على سبيل المثال، 6 على 4 يعطي نفس نتيجة 6 على 2، لأن 6-4=2.

$\begin{pmatrix}6 \\ 4 \end{pmatrix} =\cfrac{6!}{4!(6-4)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(\cancel{1\cdot 2 \cdot 3\cdot 4})\cdot (1\cdot 2)}= \cfrac{30}{2} = \bm{15}$

$\begin{pmatrix}6 \\ 2 \end{pmatrix} =\cfrac{6!}{2!(6-2)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(1\cdot 2)\cdot (\cancel{1\cdot 2 \cdot 3\cdot 4})}= \cfrac{30}{2} = \bm{15}$

مجموع رقمين اندماجيين لهما نفس البسط وبترتيبات متتالية يساوي رقم اندماجي آخر بسطه مكافئ لبسط الإضافات زائد 1 والذي يتوافق ترتيبه مع أكبر قيمة لرتب الإضافات. بمعنى آخر، يتم دائمًا استيفاء الشرط التالي:

$\begin{pmatrix}n\\ k \end{pmatrix} + \begin{pmatrix}n\\ k+1 \end{pmatrix}= \begin{pmatrix}n+1\\ k+1 \end{pmatrix}$

على سبيل المثال:

$\begin{pmatrix}9\\ 2 \end{pmatrix} + \begin{pmatrix}9\\ 3 \end{pmatrix}= \begin{pmatrix}10\\ 3 \end{pmatrix}$

تُعرف هذه الخاصية أيضًا بقاعدة باسكال.

من ناحية أخرى، يمكن أيضًا تطبيق هذه الصيغة في الاتجاه المعاكس لتحليل الرقم التوافقي إلى رقمين اندماجيين أبسط:

$\begin{pmatrix}n\\ k \end{pmatrix} = \begin{pmatrix}n-1\\ k-1 \end{pmatrix}+ \begin{pmatrix}n-1\\ k \end{pmatrix}$

على سبيل المثال، العدد التجميعي 8 على 4 يساوي 7 على 3 زائد 7 على 4:

$\begin{pmatrix}8\\ 4 \end{pmatrix} = \begin{pmatrix}7\\ 3 \end{pmatrix}+ \begin{pmatrix}7\\ 4 \end{pmatrix}$

أي رقم موجب أكبر من 1 يساوي الرقم نفسه.

$\begin{pmatrix}n\\ 1 \end{pmatrix} =n$

والسبب في هذه الخاصية هو أن مضروب الرقم يساوي مضروب الرقم السابق مضروباً في الرقم نفسه:

$\begin{pmatrix}n \\ 1 \end{pmatrix} =\cfrac{n!}{1!(n-1)!} = \cfrac{n\cdot (n-1) \cdot (n-2)\cdots 1}{(n-1) \cdot (n-2)\cdots 1}= n$

أمثلة على هذا النوع من الأعداد التوافقية:

$\begin{pmatrix}12\\ 1 \end{pmatrix} =12 \qquad \begin{pmatrix}5\\ 1 \end{pmatrix} =5 \qquad \begin{pmatrix}9\\ 1 \end{pmatrix} =9$

أي رقم موجب أكبر من 0 يساوي واحد.

$\begin{pmatrix}n\\ 0 \end{pmatrix} =1$

في الواقع، فإن مقام الكسر من هذا الرقم التوافقي سيكون دائمًا مساويًا لبسط الكسر:

$\begin{pmatrix}n\\ 0 \end{pmatrix} =\cfrac{n!}{0!(n-0)!} =\cfrac{n!}{n!} = 1$

أمثلة على الأعداد التوافقية مثل هذا:

$\begin{pmatrix}6\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}2\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}23\\ 0 \end{pmatrix} =1$

كل رقم على نفسه يساوي 1

$\begin{pmatrix}n\\ n \end{pmatrix} =1$

هنا هو العرض التوضيحي:

$\begin{pmatrix}n\\ n \end{pmatrix} =\cfrac{n!}{n!(n-n)!} =\cfrac{n!}{n!\cdot 0!}= \cfrac{n!}{n!} = 1$

أمثلة على الأعداد التوافقية مثل هذا:

$\begin{pmatrix}5\\ 5 \end{pmatrix} =1 \qquad \begin{pmatrix}37\\ 37 \end{pmatrix} =1 \qquad \begin{pmatrix}14\\ 14 \end{pmatrix} =1$

كيفية حساب رقم اندماجي مع الآلة الحاسبة

لقد رأينا حتى الآن كيفية العثور على رقم اندماجي لأرقام بسيطة إلى حد ما، ولكن عندما يتعين علينا التعامل مع كميات كبيرة جدًا، فمن الأفضل استخدام الآلة الحاسبة لتحديد الرقم التوافقي. سنرى الآن كيفية إدخال رقم اندماجي في الآلة الحاسبة.

لذا، فإن المفتاح المستخدم لحساب رقم اندماجي باستخدام الآلة الحاسبة هو مفتاح nCr . ولتحديد قيمة الرقم الاندماجي، عليك أولاً إدخال بسط الرقم الاندماجي، ثم الضغط ثانياً على مفتاح nCr، ثم إدخال ترتيب الرقم الاندماجي، وأخيراً الضغط على مفتاح يساوي.

$\begin{pmatrix}n\\ k \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} n \rightarrow \boxed{nCr} \rightarrow k \rightarrow \boxed{=}$

في الآلات الحاسبة العلمية من CASIO، عادةً ما يكون لمفتاح nCr زر خاص به أو يكون أعلى زر القسمة، حسب الطراز.

على سبيل المثال، إذا أردنا أن نعرف ما هو العدد التجميعي 10 على 6، فيجب علينا القيام بالتسلسل التالي:

$\begin{pmatrix}10\\ 6 \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} 10 \rightarrow \boxed{nCr} \rightarrow 6 \rightarrow \boxed{=} \rightarrow 210$

تطبيقات على العدد التوافقي

إذا وصلت إلى هذا الحد، فمن المحتمل أنك تعرف بالفعل كيفية حل أي رقم اندماجي، بشكل مثالي. لكن… ما هو الرقم التوافقي المستخدم؟ حسنًا، سنرى بعد ذلك كل المزايا التي يقدمها هذا النوع من العمليات الخاصة جدًا.

التوافقيات

وكما رأينا في أعلى الصفحة، نتيجة العدد التوافقي

$\begin{pmatrix}n\\ k \end{pmatrix}$

يمثل عدد المجموعات الممكنة

$k$

العناصر التي يمكن تكوينها من مجموعة من المجموع

$n$

أغراض.

لذلك، يمكن حل بعض المسائل التوافقية باستخدام الأعداد التوافقية (أو المعاملات ذات الحدين). دعونا نرى كيفية القيام بذلك باستخدام مثال:

في فصل مكون من 30 طالبًا، نريد اختيار مجموعة مكونة من 4 طلاب لتنفيذ مهام معينة. ما هو العدد الإجمالي للمجموعات المختلفة التي يمكن تشكيلها؟

في هذه الحالة لا يهم ترتيب الطلاب، فلا يتكرر نفس الطالب مرتين داخل المجموعة، ولا يدخل جميع الطلاب إلى المجموعة. لذلك، يمكن استخدام صيغة الأعداد التوافقية لتحديد عدد الطرق التي يمكن من خلالها تشكيل المجموعة.

للقيام بذلك، يجب عليك حساب العدد الاندماجي مع العدد الإجمالي للطلاب باعتباره البسط ومع عدد الطلاب الذين سيشكلون المجموعة حسب الترتيب:

$\begin{pmatrix}30 \\ 4 \end{pmatrix} =\cfrac{30!}{4!(30-4)!} =\cfrac{30\cdot 29 \cdot 28 \cdot 27 \cdot \cancel{26!}}{4\cdot 3 \cdot 2 \cdot 1 \cdot \cancel{26!}} = \cfrac{657720}{24}=\bm{27405}$

وبالتالي فإن العدد الإجمالي للمجموعات الممكنة هو 27405 مجموعة.

نيوتن ذات الحدين

تطبيق آخر للأرقام التوافقية هو ذات الحدين لنيوتن. ذات الحدين لنيوتن هي كثيرة حدود مكونة من حدين مرفوعين معًا إلى عدد صحيح، وهذا يعني أن ذات الحدين لنيوتن هي كثيرة الحدود التي تستجيب للتعبير الجبري التالي:

$(a+b)^n$

من الواضح أنه إذا كانت ذات الحدين مربعة، فهذا يعني أنها هوية بارزة ، وبالتالي يمكن حسابها بسهولة باستخدام الصيغة المقابلة. من ناحية أخرى، عندما يتم رفع ذات الحدين إلى أعداد كبيرة، يصبح الحساب صعبًا للغاية. حسنًا، تقول نظرية نيوتن ذات الحدين أن هذه الأنواع من كثيرات الحدود يمكن حسابها بسهولة شديدة من الأعداد التوافقية.

انقر على الرابط التالي واكتشف ما هي صيغة نيوتن ذات الحدين وكيف يتم حسابها. بالإضافة إلى ذلك، ستتمكن من رؤية الأمثلة والتدرب على التمارين التي تم حلها خطوة بخطوة. وأخيرا، سوف تكتشف التاريخ الغريب لهذه النظرية.

مثلث تارتاجليا (أو مثلث باسكال).

كما رأيت خلال هذه المقالة، فإن حساب معامل ذات الحدين للأعداد الكبيرة يدويًا يمكن أن يكون شاقًا ومعقدًا.

من ناحية أخرى، مع مثلث تارتاليا، والذي يسمى أيضًا مثلث باسكال، يمكن تحديد جميع الأرقام التوافقية بسهولة باستخدام قاعدة ذاكري. وهذا مفيد جدًا منطقيًا لأنه يوفر الكثير من الوقت أثناء العمليات الحسابية.

لمعرفة كيفية القيام بذلك بالضبط، راجع شرح مثلث تارتاليا . في هذه الصفحة المرتبطة، ستكتشف ما هو هذا المثلث الغامض، وفيم يستخدم (له تطبيقات مدهشة) 😮 وما هو أصله (لقد تم استخدامه بالفعل منذ أكثر من 1000 عام).

حل تمارين الأعداد التوافقية

لكي تتمكن من التدرب على المفاهيم الموضحة وفهمها بشكل كامل، نترك لك العديد من التمارين التي تم حلها خطوة بخطوة حول الأعداد التوافقية.

التمرين 1

ابحث عن الرقم التجميعي 9 في 5 (بدون استخدام الآلة الحاسبة).

انظر الحل

للعثور على قيمة العدد الاندماجي 9 من أصل 5، نقوم ببساطة بتطبيق الصيغة المضروب:

$\begin{pmatrix}9 \\ 5 \end{pmatrix} =\cfrac{9!}{5!(9-5)!} = \cfrac{9\cdot 8 \cdot 7\cdot 6\cdot \cancel{5!}}{\cancel{5!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{3024}{24} = \bm{126}$

تمرين 2

ما هو نتيجة المجموع التالي لعددين اندماجيين؟ (بدون حاسبة)

$\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}$

انظر الحل

من خصائص الأعداد التوافقية يتبين أن مجموع المسألة يساوي العدد التوافقي التالي:

$\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}=\begin{pmatrix}11\\ 7 \end{pmatrix}$

لذلك يكفي حساب الرقم التوافقي 11 من 7:

$\begin{pmatrix}11 \\ 7 \end{pmatrix} =\cfrac{11!}{7!(11-7)!} = \cfrac{11\cdot 10 \cdot 9\cdot 8 \cdot \cancel{7!}}{\cancel{7!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{7920}{24} = \bm{330}$

التمرين 3

حدد ما إذا كانت الأعداد التوافقية التالية متساوية:

$\begin{pmatrix}6\\ 0 \end{pmatrix} \qquad \begin{pmatrix}6\\ 1 \end{pmatrix}\qquad \begin{pmatrix}6\\ 6 \end{pmatrix}$

انظر الحل

للعثور على نتيجة الأعداد الاندماجية الثلاثة، لا تحتاج إلى استخدام الآلة الحاسبة، ولكن يمكن العثور عليها بسهولة بفضل خصائص الأعداد التوافقية.

أولًا، أي رقم اندماجي لأي رقم أكبر من 0 يعطي 1. لذلك:

$\begin{pmatrix}6\\ 0 \end{pmatrix} =1$

ومن ناحية أخرى، أي عدد أكبر من واحد يساوي العدد نفسه. حتى الآن:

$\begin{pmatrix}6\\ 1 \end{pmatrix} =6$

وأخيرًا، أي رقم اندماجي مكون من نفس العدد مكررًا مرتين يساوي 1. إذن:

$\begin{pmatrix}6\\ 6 \end{pmatrix} =1$

وفي الختام فإن العددين الاندماجيين الأول والثالث في المسألة متساويان، إلا أنهما مختلفان عن العدد التوافقي الأوسط.

$\begin{pmatrix}6\\ 0 \end{pmatrix}= \begin{pmatrix}6\\ 6 \end{pmatrix}\neq \begin{pmatrix}6\\ 1 \end{pmatrix}$

الرقم التوافقي (أو معامل ذو الحدين)

ما هو الرقم التوافقي؟

صيغة العدد التوافقي

مثال لحساب رقم اندماجي

خصائص العدد التوافقي

كيفية حساب رقم اندماجي مع الآلة الحاسبة

تطبيقات على العدد التوافقي

التوافقيات

نيوتن ذات الحدين

مثلث تارتاجليا (أو مثلث باسكال).

حل تمارين الأعداد التوافقية

التمرين 1

تمرين 2

التمرين 3

اترك تعليقاً إلغاء الرد