في هذه الصفحة سوف تكتشف ما هو وكيفية حساب القيمة العددية لكثيرة الحدود. بالإضافة إلى ذلك، ستتمكن من رؤية أمثلة وتمارين تم حلها خطوة بخطوة للقيمة العددية لكثيرة الحدود.
ما هي القيمة العددية لكثيرة الحدود؟
في الرياضيات، القيمة العددية لكثيرة الحدود P(x) للقيمة x=a، أي P(a)، هي النتيجة التي يتم الحصول عليها عن طريق استبدال المتغير x لكثيرة الحدود بالرقم a وإجراء الحسابات المشار إليها في التعبير متعدد الحدود.
لكي تتمكن من فهم مفهوم القيمة العددية لكثيرة الحدود بشكل أفضل، نوضح أدناه كيفية حسابها بمثال:
كيفية حساب القيمة العددية لكثيرة الحدود
الآن بعد أن عرفنا التعريف الرياضي للقيمة العددية لكثيرة الحدود، دعونا نرى كيفية تحديد القيمة العددية لكثيرة الحدود باستخدام مثال:
- ما هي القيمة العددية لمتعددة الحدود التالية لـ x=2؟
![]()
للعثور على القيمة العددية لكثيرة الحدود، من الضروري تقييم كثيرة الحدود المذكورة بالقيمة المعطاة في المشكلة، أي أنه من الضروري استبدال المتغير
![]()
من كثير الحدود بقيمة البيان. ولذلك، في هذه الحالة نحن بحاجة إلى استبدال الرسالة
![]()
ل 2:
![]()
وبمجرد التعويض بالقيمة في المقدار الجبري لكثيرة الحدود، فإننا نجري العمليات. لذلك نحل أولا للقوى:
![]()
الآن نحسب الضرب:
![]()
وأخيرًا، نجمع ونطرح الحدود:
![]()
في الختام، القيمة العددية لكثيرة الحدود لـ x=2 تساوي 21.
كما ترون، فإن العثور على القيمة العددية لكثيرة الحدود ليس أمرًا معقدًا للغاية، ولكنه يحتوي على بعض التطبيقات المفيدة جدًا. على سبيل المثال، معرفة كيفية إيجاد القيمة العددية لكثيرة الحدود أمر ضروري للتمكن من استخدام نظرية الباقي، وهي نظرية مهمة جدًا حول كثيرات الحدود. اضغط على هذا الرابط واكتشف ما هي نظرية الباقي ، وستجد شرحها وأمثلة على استخدامها وتمارين محلولة خطوة بخطوة.
أمثلة على القيم العددية لكثيرات الحدود
لكي تفهم كيفية الحصول على القيمة العددية لكثيرة الحدود، نتركك مع أمثلة أخرى محلولة:
مثال 1
- احسب القيمة العددية لكثيرة الحدود
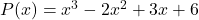
ل

![Rendered by QuickLaTeX.com \begin{aligned} P(-1) & =(-1)^3-2\cdot (-1)^2+3\cdot (-1)+6 \\[2ex] & = -1-2\cdot 1+3\cdot (-1)+6 \\[2ex] & =-1-2-3+6 \\[2ex]&= \bm{0} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3293713c5e12fac56d94be90f6bfc6e5_l3.png)
في هذه الحالة، القيمة العددية لكثيرة الحدود تساوي 0. وهذا له عواقب بسبب خصائص كثيرات الحدود، لأنه بفضل نظرية العامل يمكننا معرفة ما تبقى من أقسام معينة بين كثيرات الحدود. ولمعرفة المزيد اضغط على الرابط السابق حيث نشرح ما هي هذه النظرية وما الهدف منها.
مثال 2
- تحديد القيمة العددية لكثيرة الحدود
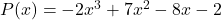
ل
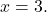
![Rendered by QuickLaTeX.com \begin{aligned} P(3) & =-2\cdot 3^3+7\cdot 3^2-8\cdot 3-2 \\[2ex] & =-2\cdot 27+7\cdot 9-8\cdot 3-2 \\[2ex] & =-54+63-24-2 \\[2ex]&= \bm{-17} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ad8b1145d569157b4e771adfae674e2c_l3.png)
لم نرى حتى الآن سوى كيفية تحديد القيمة العددية لكثيرة الحدود بالطريقة الكلاسيكية، ولكن يجب أن تعلم أن هناك طريقة أخرى. وبشكل أكثر تحديدًا، يمكنك أيضًا حساب القيمة العددية لكثيرة الحدود باستخدام طريقة روفيني . يجب عليك أيضًا معرفة كيفية استخدام هذا الإجراء، لذا ننصحك بمراجعة شرحه التفصيلي في الرابط.
القيمة العددية لكثيرة الحدود بمتغيرين أو أكثر
لقد رأينا للتو كيفية إيجاد القيمة العددية لكثيرة الحدود عندما تحتوي على متغير واحد فقط. لكن… كيف يمكنك الحصول على القيمة العددية لكثيرة الحدود عندما تحتوي على أكثر من متغير واحد؟
حسنًا، إذا كان كثير الحدود يحتوي على حرفين أو أكثر، فيجب حساب قيمته العددية بنفس الطريقة، أي أولاً استبدل كل متغير في كثير الحدود بالقيمة المقابلة له ثم حل العمليات كثيرة الحدود .
على سبيل المثال، لديك مشكلة من هذا النوع تم حلها أدناه:
- أوجد القيمة العددية لكثيرة الحدود متعددة المتغيرات
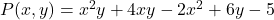
للقيم
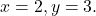
أولا نستبدل كل متغير بالقيمة المقابلة له، أي نستبدل الحرف
![]()
لمدة 2 ونغير الحرف
![]()
بحلول 3:
![]()
نحن نحل للقوى:
![]()
الآن نحسب المنتجات:
![]()
وأخيرًا نقوم بعمليات الجمع والطرح:
![]()
وبالتالي فإن القيمة العددية لكثيرة الحدود لبيانات التعليمات تعادل 41.
تمارين محلولة على القيمة العددية لكثيرة الحدود
التمرين 1
ما هي القيمة العددية لمتعددة الحدود P(x) لـ x=-2؟
![]()
للعثور على القيمة العددية لكثيرة الحدود، نحتاج ببساطة إلى استبدال القيمة الواردة في العبارة في تعبير كثير الحدود وحل العمليات الناتجة:
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =-2\cdot (-2)^3-4\cdot (-2)^2+3\cdot (-2)+8 \\[2ex] & =-2\cdot (-8)-4\cdot 4+3\cdot (-2)+8 \\[2ex] & =+16-16-6+8 \\[2ex]&= \bm{2} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-93b7cf1a6c7e930a0a70fc8302f4012d_l3.png)
تمرين 2
احسب القيمة العددية لمتعددة الحدود التالية باستخدام الكسور x=4.
![]()
سواء كانت كثيرة الحدود تحتوي على كسور أم لا، فإن الإجراء الخاص بإيجاد القيمة العددية لكثيرة الحدود هو نفسه دائمًا. لذلك يجب علينا استبدال المتغير x بـ 4 وحل الحسابات:
![Rendered by QuickLaTeX.com \begin{aligned} P(4) & =\cfrac{1}{2} \cdot 4^2-\cfrac{5}{4}\cdot 4+ 7 \\[2ex] & =\cfrac{1}{2} \cdot 16-\cfrac{5}{4}\cdot 4+ 7\\[2ex] & =8-5+7 \\[2ex]&= \bm{10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04fa4389b5e7c5257937ad35aed07c7b_l3.png)
التمرين 3
تحديد القيمة العددية لكثيرة الحدود للقيم x=3 وy=5 وz=-2
![]()
لتحديد القيمة العددية لكثيرة الحدود متعددة المتغيرات، يكفي استبدال القيم الواردة في المشكلة في التعبير الجبري وحل العمليات الناتجة:
![Rendered by QuickLaTeX.com \begin{aligned} P(3,5,-2) & =3^2\cdot 5\cdot (-2)+4\cdot 5^2\cdot (-2)^2-3\cdot 3^2\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =9\cdot 5\cdot (-2)+4\cdot 25\cdot 4-3\cdot 9\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =-90+400+54-180\\[2ex]&= \bm{184} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-29683a91c14427a8ea42c3518e59e53f_l3.png)
التمرين 4
بالنظر إلى كثير الحدود
![]()
حساب قيمة المعلمة
![]()
لهذا السبب.
![]()
في هذه المسألة إيجاد قيمة المجهول
![]()
نحن بحاجة إلى حل المعادلة
![]()
![]()
لذلك، نحاول أولاً حساب قيمة P(-2):
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =-2\cdot (-2)^3-3\cdot (-2)^2+5\cdot (-2)+k \\[2ex] & =-2\cdot (-8)-3\cdot 4+5\cdot (-2)+k \\[2ex] & =+16-12-10+k\\[2ex]&=-6+k \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b58398099c8033b93a559e2f0c87f1a_l3.png)
الآن نقوم بمساواة التعبير الذي تم الحصول عليه بـ 5:
![]()
![]()
وأخيرًا نحل المعادلة الناتجة:
![]()
![]()