كيفية تحليل كثيرات الحدود (تحليل كثيرات الحدود) -

في هذه الصفحة نشرح كيفية تحليل أي نوع من كثيرات الحدود. سنرى أولاً كيفية تحليل كثيرات الحدود باستخدام قاعدة روفيني، ثم سننتقل إلى كيفية تحليل كثيرات الحدود التي لا تحتوي على حد مستقل، ثم سنقوم بتحليل تحليلات كثيرات الحدود الجذرية بالكسور، وأخيرًا، الحالات الخاصة للتحليلات (أبرزها الهويات، والتحليل عن طريق التجميع، وثلاثيات الحدود، وما إلى ذلك). تم تقديم جميع الشروحات باستخدام الأمثلة، وبالإضافة إلى ذلك، في النهاية، ستتمكن من التدرب على حل التمارين خطوة بخطوة لتحليل كثيرات الحدود.

ما هو التحليل متعدد الحدود؟

تحليل كثيرات الحدود هو أسلوب يستخدم في الرياضيات لتحليل كثيرات الحدود إلى حاصل ضرب العوامل.

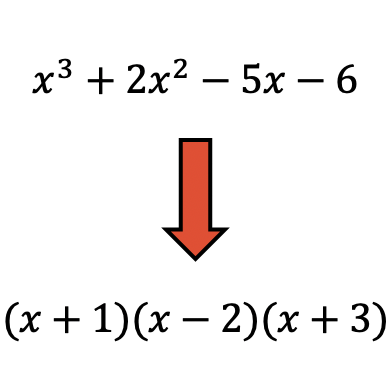
تحليل كثيرات الحدود (تحليل كثيرات الحدود)

يعد تحليل كثيرات الحدود إلى عوامله مفيدًا جدًا لأنه من الأسهل إجراء العمليات باستخدام كثيرات الحدود التحليلية.

الآن بعد أن عرفنا ما هو تحليل كثيرات الحدود، دعونا نرى كيف يتم تحليل كثيرات الحدود.

كيفية تحليل كثيرات الحدود إلى عوامل مع قاعدة روفيني

من الواضح، لفهم كيفية تحليل كثيرة الحدود إلى عوامل مع قاعدة روفيني، يجب عليك أولاً معرفة كيفية تطبيق قاعدة روفيني . لذلك نترك لك هذا الرابط في حالة رغبتك في مراجعة شكل الإجراء أولاً.

لتحليل كثير الحدود، يجب اتباع الخطوات التالية:

يتم حساب جذور كثير الحدود وفقًا لقاعدة روفيني.
يتم التعبير عن كل جذر من النوع x=a على شكل عامل (xa).
كثير الحدود المُحلل هو حاصل ضرب جميع العوامل الموجودة في معامل الحد الأعلى من كثير الحدود غير الموزون.

لكي تتمكن من رؤية كيفية القيام بذلك وفهم إجراء تحليل كثيرات الحدود بشكل أفضل، ستجد أدناه مثالًا ملموسًا مشروحًا خطوة بخطوة:

عامل متعدد الحدود التالي:

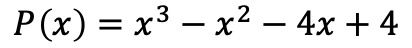
أول ما يجب فعله هو حساب جذور أو أصفار كثيرة الحدود. للقيام بذلك، نحتاج إلى إيجاد مقسومات الحد المستقل لكثيرة الحدود ، والتي في هذه الحالة هي ±1، ±2 و±4.

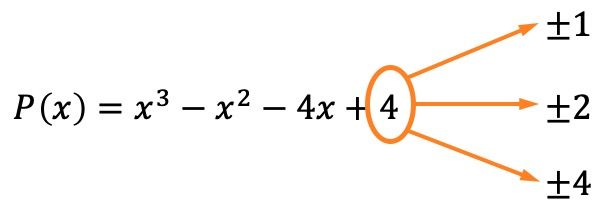
الآن نعلم، بفضل نظرية الباقي والعوامل، أنه إذا كان باقي قسمة كثيرة الحدود على إحدى هذه القيم يساوي 0، فهذا يعني أن القيمة المذكورة هي جذر لكثيرة الحدود.

لذلك يجب علينا قسمة كثيرة الحدود على كل من مقسومات الحد المستقل بقاعدة روفيني ومعرفة أي الحالات يكون الباقي صفرًا.

على سبيل المثال، نبدأ بتطبيق قاعدة روفيني مع

$x=+1:$

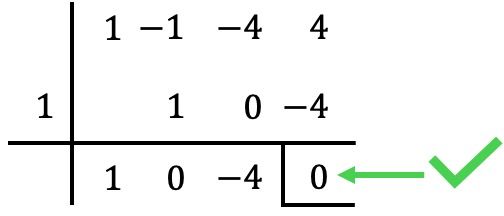
في هذه الحالة، يكون باقي (أو بقايا) القسمة صفرًا

$x=1$

وهو جذر كثير الحدود. ✅

حسنًا، لدينا بالفعل جذر كثيرة الحدود، وكل ما تبقى هو تحديد الجذور الأخرى المتبقية. للقيام بذلك، نستخدم قاعدة روفيني مع مقسوم آخر على الحد المستقل، على سبيل المثال

$x=-1.$

أيضًا، ليست هناك حاجة لاستخدام طريقة روفيني مع العدد الصحيح كثير الحدود، ولكن يمكننا الاستمرار من حيث توقفنا في الخطوة السابقة:

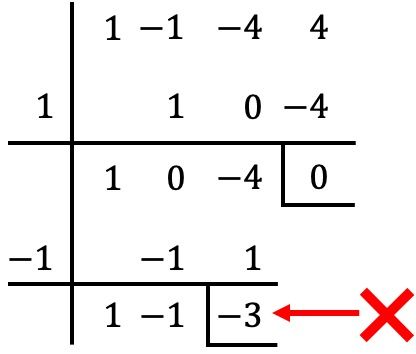
ومع ذلك، في هذه الحالة، عند القسمة على

$x=-1$

والباقي الذي تم الحصول عليه يختلف عن 0، لذلك

$x=-1$

إنه ليس جذرًا لكثيرة الحدود. ❌

لذلك يجب علينا أن نجرب قيمة أخرى، على سبيل المثال نستخدم قاعدة روفيني

$x=+2:$

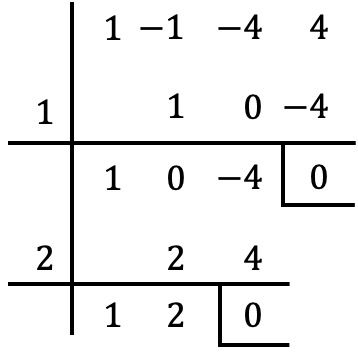
في هذه الحالة، نحصل مرة أخرى على صفر باقي، إذن

$x=2$

وهو أيضًا جذر متعدد الحدود.

ونستمر في تطبيق نفس الإجراء. الآن نتحقق مما إذا كان

$x=-2$

هل هو جذر كثير الحدود أم لا:

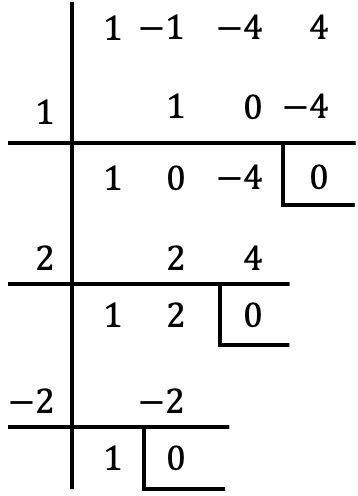
بالقسمة على

$x=-2$

وبقاعدة روفيني نحصل على باقي صفر

$x=-2$

هو جذر أو صفر لكثيرة الحدود.

لذلك لم يعد بإمكاننا الاستمرار في تطبيق قاعدة روفيني، لذلك وجدنا بالفعل جميع جذور كثيرة الحدود، وهي:

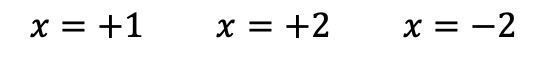
بمجرد تحديد جميع جذور كثيرة الحدود، يمكننا تحليلها. للقيام بذلك، ما عليك سوى التعبير عن كل جذر

$x=a$

على شكل عامل من النوع

$(x-a)$

، وهذا يعني أنه يجب وضع قوس مع a لكل جذر

$x$

وتغير الجذر علامة:

والآن بعد أن أصبح لدينا جميع الجذور معبرًا عنها كعوامل، يجب علينا ضرب جميع الأقواس في معامل الحد الأعلى من الدرجة الأعلى لكثيرة الحدود الأصلية:

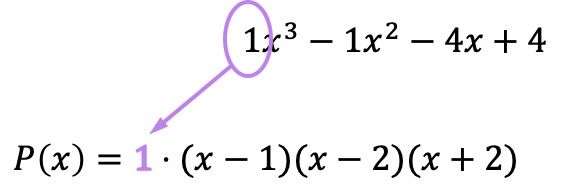
على الرغم من أن المعامل في هذه الحالة هو 1، وبالتالي لا يؤثر على النتيجة، فمن المهم أن تتذكر القيام بهذا الضرب. نظرًا لأنه إذا كان المعامل المذكور مختلفًا عن 1، فإن كثيرة الحدود المُحللة ستتغير، وبالتالي، من خلال عدم إدخال الرقم، سنرتكب خطأ في تحليل كثيرة الحدود.

باختصار، متعدد الحدود المُعامل هو:

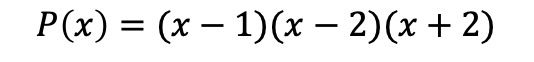
تحليل كثيرات الحدود بدون حد مستقل

لقد رأينا للتو أن الحد المستقل مهم لتحليل كثيرات الحدود، لأنه يسمح لنا بتحديد الجذور المحتملة لكثيرة الحدود. ومع ذلك، كيف يمكنك تحليل كثيرة الحدود التي ليس لها حد مستقل؟

لتحليل كثيرة الحدود بدون حد مستقل ، يجب أولاً استخراج العامل المشترك لكثيرة الحدود، ثم استخراج جذور كثيرة الحدود بدون العامل المشترك باستخدام قاعدة روفيني.

قد يبدو الأمر معقدًا بعض الشيء إذا كتب بهذه الطريقة، لذا دعونا نحل مثالًا خطوة بخطوة حتى تتمكن من معرفة كيفية تحليل كثيرة الحدود بعامل مشترك:

قم بإجراء التحليل العاملي لمتعددة الحدود التالية:

$P(x) = x^4-3x^3-x^2+3x$

كما ترون، كثيرة الحدود في المشكلة ليس لها حد مستقل، لذلك علينا أن نأخذ العامل المشترك لكثيرة الحدود. إذا نظرنا عن كثب، فسنجد أن جميع عناصر كثيرة الحدود تحتوي على عنصر واحد على الأقل

$x,$

وبالتالي فإن العامل المشترك هو

$x.$

لذلك، عند استخراج العامل المشترك من كثيرة الحدود، ننتهي بالتعبير التالي:

$P(x) = x\left(x^3-3x^2-x+3\right)$

وبمجرد أن نستخرج العامل المشترك لكثيرة الحدود، فإننا نطبق قاعدة روفيني لحساب جذور كثيرات الحدود المجمعة بين قوسين (بالإجراء الذي رأيناه في القسم السابق):

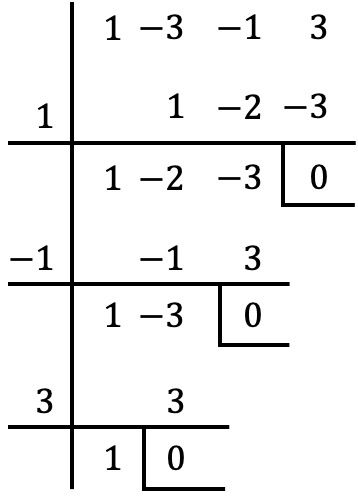
لذا فإن جذور أو أصفار كثيرة الحدود الموجودة بين قوسين هي:

$\bm{x=+1 \qquad x=-1 \qquad x=+3}$

لذلك، لتحليل كثيرة الحدود، ما عليك سوى استبدال كثيرة الحدود الموجودة بين قوسين بجذورها في شكل عامل (كما هو موضح في القسم أعلاه):

$\begin{array}{c}P(x) = x\left(x^3-3x^2-x+3\right) \\[2ex]\color{red} \bm{\downarrow} \\[2ex] \bm{P(x) = x(x-1)(x+1)(x-3)}\end{array}$

وبهذه الطريقة قمنا بالفعل بتحليل كثيرة الحدود التي لم يكن لها حد من الدرجة 0. لاحظ أن الفرق الوحيد هو أنه يتعين علينا استخراج عامل مشترك أولاً، ولكن جميع الخطوات التالية هي نفسها تمامًا.

ومن ناحية أخرى، عليك أن تعرف ذلك

$x=0$

وهو أيضًا جذر لكثيرة الحدود، حيث أننا عندما نستخرج العامل المشترك، فهذا يعني أن أحد جذور كثير الحدود هو

$x=0.$

إذن، جميع جذور كثيرة الحدود هي كما يلي:

$\bm{x= 0 \qquad x=+1 \qquad x=-1 \qquad x=+3}$

في الواقع، يجب أن يكون لكثيرة الحدود العديد من الجذور التي تشير إليها درجتها. في هذه الحالة يكون كثير الحدود من الدرجة 4 وبالتالي له 4 جذور.

تحليل كثيرات الحدود ذات الجذور العقلانية

لقد رأينا حتى الآن أمثلة على تحليل كثيرات الحدود إلى عوامل ذات جذور صحيحة، ومع ذلك، يمكن أن يكون لكثيرة الحدود أيضًا جذور نسبية، أي مع الكسور. دعونا نرى كيف يتم حل هذا النوع من العوامل متعددة الحدود بمثال:

قم بتحليل كثيرة الحدود غير الكاملة التالية:

$P(x) = 4x^3-7x+3$

كما هو الحال دائمًا، نستخدم قاعدة روفيني مع مقسومات الحد المستقل لمحاولة تحديد جذور كثيرة الحدود:

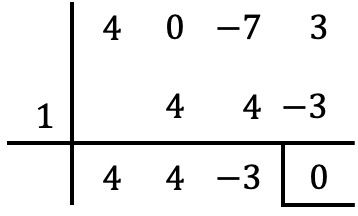
تحليل كثيرات الحدود ذات الجذور العقلانية

لكن لا يمكننا حساب المزيد من الجذور باستخدام Ruffini، لأننا إذا حاولنا حساب Ruffini مع جميع أرقام المقسوم عليه الأخرى للمصطلح المستقل، فسنحصل على باقي غير الصفر.

ولذلك نجد أنفسنا في وضع حيث أنه فقط مع

$x=1$

ما تبقى من القسمة يعادل 0، وهذا يعني أن كثير الحدود يمكن أن يكون له جذور كسرية. لتحديد هذه الجذور يمكننا تطبيق روفيني مع الكسور، ومع ذلك، فمن السهل جدًا ارتكاب أخطاء في الحسابات ولهذا السبب نقوم عادةً في هذه الحالات بما يلي:

عندما لا نستطيع الاستمرار في تطبيق قاعدة روفيني مع الجذور الصحيحة، يجب علينا أن نجعل آخر كثير حدود تم الحصول عليه يساوي 0 ونحل المعادلة الناتجة. وبالتالي فإن جذور كثيرة الحدود ستكون القيم الموجودة في المعادلة.

من ناحية أخرى، إذا لم يكن للمعادلة حل، فهذا يعني أن كثيرة الحدود لم يعد لها جذور، وبالتالي لا يمكن تحليلها بالكامل.

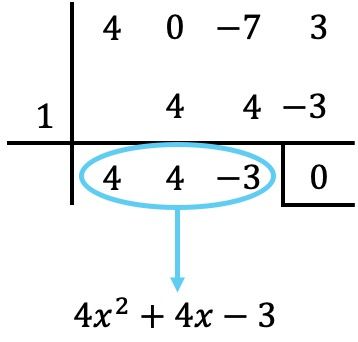
ولذلك فإننا نجعل حاصل القسمة كثير الحدود يساوي الصفر:

$4x^2+4x-3=0$

ونستخدم صيغة المعادلة التربيعية لحل المعادلة الناتجة:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-4 \pm \sqrt{4^2-4\cdot 4\cdot (-3)}}{2\cdot 4}= \cfrac{-4\pm \sqrt{16+48}}{8} = \cfrac{-4 \pm\sqrt{64}}{8}$

$\displaystyle x = \cfrac{-4 \pm 8}{8} = \begin{cases} \cfrac{-4+8}{8} = \cfrac{4}{8} = \cfrac{1}{2} \\[4ex]\cfrac{-4-8}{8} = \cfrac{-12}{8} = -\cfrac{3}{2} \end{cases}$

وبالتالي فإن جذور كثير الحدود هي:

$x=+1 \qquad x=\cfrac{1}{2} \qquad x=-\cfrac{3}{2}$

ولذلك فإن كثيرة الحدود لها جذور في شكل كسور.

وبمجرد أن نعرف جميع جذور كثيرة الحدود، يمكننا بسهولة إيجاد كثيرة الحدود المحللة عن طريق التعبير عن كل جذر

$x=a$

على شكل عامل من النوع

$(x-a)$

، وهذا يعني أنه يجب وضع قوس مع a لكل جذر

$x$

وتغير الجذر علامة:

$\displaystyle P(x)= 4\left(x-1\right)\left(x-\frac{1}{2}\right)\left(x+\frac{3}{2}\right)$

تذكر أنه لتحليل كثيرة الحدود، يجب عليك أيضًا ضرب عواملها في معامل الحد الأعلى من كثيرة الحدود غير المحللة، وهو في هذه الحالة 4.

حالات خاصة من العوملة كثيرات الحدود

عادة، يتم استخدام قاعدة روفيني (أو القسمة التركيبية) لتحليل كثيرة الحدود، كما هو موضح أعلاه. لكن اعتمادًا على كثيرة حدود المشكلة، يمكنك في بعض الأحيان إجراء تحليل كثيرات الحدود بشكل أسرع. سنرى كل حالة من هذه الحالات المحددة أدناه.

تحليل الهويات البارزة

إذا رأينا أن كثيرة الحدود تتوافق مع هوية بارزة (أو منتج بارز)، فمن السهل جدًا تحليلها. ومع ذلك، لتتمكن من القيام بذلك، يجب عليك إتقان صيغ الهويات البارزة ، وإلا فإنني أوصي بإلقاء نظرة على هذا الرابط حيث لن تجد الصيغ فحسب، بل ستتمكن أيضًا من رؤية أمثلة للهويات البارزة. الهويات ويمكنك حتى ممارسة التمارين معهم حلها خطوة بخطوة.

فرق المربعات

كما تعلمون جيدًا، فإن صيغة الهوية البارزة لفرق المربعات هي كما يلي:

$a^2-b^2=(a+b)\cdot (a-b)$

ولذلك، إذا وجدنا كثير الحدود الذي يفي بالتعبير

$a^2-b^2$

يمكن أن تؤخذ في الاعتبار مباشرة.

انظر إلى المثال التالي الذي يؤخذ فيه اختلاف المربعات بعين الاعتبار:

$x^2-9 = (x+3)(x-3)$

من ناحية أخرى، فإن جذور كثير الحدود هي:

$x=-3 \qquad x=+3$

أمثلة أخرى على تحليل ذوات الحدين التي تمثل اختلافات في المربعات:

$x^2-4=(x+2)(x-2) \quad \longrightarrow \quad \text{ra\'ices: } x=-2, +2$

$x^2-16=(x+4)(x-4) \quad \longrightarrow \quad \text{ra\'ices: } x=-4, +4$

$x^2-25=(x+5)(x-5) \quad \longrightarrow \quad \text{ra\'ices: } x=-5, +5$

مربع الجمع والطرح

يجب أن تعرف بالفعل معادلات المتطابقتين الرئيسيتين المتبقيتين: مربع الجمع ومربع الطرح.

ساحة المبلغ

$a^2+2ab+b^2 = (a+b)^2$

مربع الطرح

$a^2-2ab+b^2= (a-b)^2$

لذا، إذا أدركنا أن كثيرة الحدود تقابل إحدى هاتين المتطابقتين البارزتين، فيمكننا تحليلها بشكل مباشر. انظر إلى الأمثلة التالية:

$x^2+6x+9 = (x+3)^2$

الجذر المزدوج:

$x=-3$

$x^2-8x+16 = (x-4)^2$

الجذر المزدوج:

$x=4$

يعد تحديد أنواع المنتجات البارزة هذه أكثر صعوبة قليلاً. الحيلة هي التحقق مما إذا كان الحد المستقل لكثيرة الحدود هو مربع رقم ما، وإذا كان الحد الأعلى هو مربع أحادي الحد (عادةً

$x$

)، في هذه الحالة يكفي التحقق من صحة ذلك

$2ab$

يعادل نهاية الدبلوم المتوسط .

على سبيل المثال، إذا كان لدينا متعدد الحدود التالي:

$x^2+10x+25$

في هذه الحالة، يمكن أن يكون فقط مربع المجموع، لأن جميع عناصر كثيرة الحدود موجبة. لذلك المتغير

$b$

يجب أن تكون الصيغة 5، لأنها جذر الحد المستقل والمتغير

$a$

يجب ان يكون

$x$

لأنه أصل اللفظ قد درجة.

$a=\sqrt{x^2} = x$

$b=\sqrt{25} = 5$

كل ما علينا فعله الآن هو إثبات أن صيغة مربع المجموع تتحقق مع حد الدرجة المتوسطة:

$2ab = 10x \ \color{blue} \bm{?}$

$2ab = 2\cdot x \cdot 5 = 10 x$

✅

تم استيفاء صيغة المنتج البارز، وبالتالي فإن كثيرة الحدود المحللة هي:

$x^2+10x+25 = (x+5)^2$

وجذر كثيرة الحدود هذه هو

$x=-5,$

وهو جذر مزدوج لأن عامله مربع (يتكرر مرتين).

فيما يلي المزيد من الأمثلة على تحليل ثلاثيات الحدود المربعة الكاملة:

$x^2-4x+4=(x-2)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=+2$

$x^2+14x+49=(x+7)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=-7$

$9x^2-12x+4=(3x-2)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=+\cfrac{2}{3}$

تحليل ثلاثيات الحدود من الدرجة الثانية

كما رأينا للتو، توجد أحيانًا ثلاثيات حدود تكون عبارة عن مربعات كاملة ويمكن تحليلها مباشرةً باستخدام صيغ المتطابقات البارزة. لكن معظم ثلاثيات الحدود ليست منتجات بارزة، فكيف يمكننا تحليل حالات كثيرات الحدود هذه؟

لتحليل كثير الحدود التربيعية، ليس من الضروري تطبيق طريقة روفيني، فقط قم بمساواة كثير الحدود بالصفر وحل المعادلة التربيعية الناتجة. وبالتالي فإن حلول المعادلة ستكون جذور كثيرة الحدود.

على سبيل المثال، إذا طُلب منا تحليل كثيرة الحدود التالية من الدرجة 2:

$P(x) = x^2+2x-15$

بدلاً من استخدام Ruffini، قمنا بتعيين كثير الحدود يساوي 0:

$x^2+2x-15=0$

والآن نستخدم صيغة معادلة الدرجة الثانية لإيجاد حلول المعادلة:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-2 \pm \sqrt{2^2-4\cdot 1\cdot (-15)}}{2\cdot 1}= \cfrac{-2\pm \sqrt{4+60}}{2} = \cfrac{-2 \pm\sqrt{64}}{2}$

$\displaystyle x = \cfrac{-2 \pm 8}{2} = \begin{cases} \cfrac{-2+8}{2} = \cfrac{6}{2} = 3 \\[4ex]\cfrac{-2-8}{2} = \cfrac{-10}{2} = -5 \end{cases}$

وبالتالي فإن جذور كثير الحدود هي:

$x=3 \qquad x=-5$

وأخيرًا، تحليل متعدد الحدود هو:

$P(x) =(x-3)(x+5)$

تحليل ثلاثية الحدود من الدرجة الرابعة مع الأسس الزوجية

كما في الحالة السابقة، لتحليل كثيرة الحدود من الدرجة الرابعة ذات أسس زوجية، نحتاج إلى جعل كثيرة الحدود مساوية للصفر وحل المعادلة الثنائية. بحيث تتوافق القيم الموجودة مع جذور كثيرة الحدود.

على سبيل المثال، سنقوم بتحليل كثيرة الحدود التالية من الدرجة 4:

$P(x) =x^4-5x^2+4$

أولاً، نجعل كثيرة الحدود تساوي الصفر:

$x^4-5x^2+4=0$

الآن علينا حل المعادلة الثنائية. للقيام بذلك، نقوم بإجراء تغيير متغير:

$x^2=t$

$t^2-5t+4=0$

نحل المعادلة التربيعية بالصيغة:

$t= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$t= \cfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1}= \cfrac{5\pm \sqrt{25-16}}{2} = \cfrac{5 \pm\sqrt{9}}{2}$

$\displaystyle t = \cfrac{5 \pm 3}{2} = \begin{cases} \cfrac{5+3}{2} = \cfrac{8}{2} = 4 \\[4ex]\cfrac{5-3}{2} = \cfrac{2}{2} = 1 \end{cases}$

نلغي تغيير المتغير لحساب الجذور:

$x^2=t$

$x^2=4$

$x=\sqrt{4}$

$x=\pm 2$

$x^2=1$

$x=\sqrt{1}$

$x=\pm 1$

وبالتالي فإن جذور كثير الحدود هي:

$x=+2 \qquad x=-2 \qquad x=+1 \qquad x=-1$

وبمجرد أن نعرف جذور أو أصفار كثيرة الحدود، فإننا نقوم بتحليلها من خلال التعبير عن جذورها جبريًا في صورة عوامل:

$P(x) =(x-1)(x+1)(x-2)(x+2)$

تحليل كثيرات الحدود عن طريق التجميع

في بعض الحالات الخاصة جدًا، يمكن استخدام صيغة لتحليل نوع معين من كثيرات الحدود.

إذا كان لدينا كثيرة الحدود بالشكل التالي:

$x^2-ax- bx+ab$

يمكننا تبسيط كثيرة الحدود عن طريق إزالة العامل المشترك:

$x^2-ax- bx+ab = x(x-a)-b(x-a)$

ويمكن تبسيط كثير الحدود بشكل أكبر عن طريق استخراج العامل المشترك مرة ثانية:

$x(x-a)-b(x-a) =(x-a)\cdot (x-b)$

بهذه الطريقة تمكنا من تحليل كثير الحدود إلى عوامل دون تطبيق روفيني أو أي طريقة أخرى. وجذور كثيرة الحدود المذكورة ستكون:

$x=a \qquad x=b$

والآن لنرى هذه الطريقة بمثال عددي:

$x^2-3x-2x+6$

أولا، نحذف العامل المشترك مع

$x$

ومع 2:

$x^2-3x-2x+6 = x(x-3)-2(x-3)$

ومثل الآن

$(x-3)$

هو عامل مشترك لكثيرة الحدود، نستخرج العامل المشترك لـ

$(x-3):$

$x(x-3)-2(x-3)=(x-3)\cdot (x-2)$

وبالتالي فإن جذور كثير الحدود هي:

$x=3 \qquad x=2$

وتسمى هذه الطريقة أيضًا بتحليل كثيرات الحدود عن طريق استخلاص العامل المشترك المزدوج. على الرغم من أن هذا إجراء سريع جدًا، إلا أننا لا ننصح بإجراء هذا النوع من التحليل لأنه يتم الإبلاغ عن الأخطاء بشكل متكرر عند التخصيم بهذه الطريقة. بالإضافة إلى ذلك، كما رأينا أعلاه، يمكن أيضًا تحليل كثيرة الحدود من الدرجة الثانية عن طريق حل معادلة تربيعية بسيطة. باختصار، لن يحدث شيء إذا لم تفهم هذه الطريقة جيدًا.

أخيرًا، تجدر الإشارة إلى أنه لا تزال هناك طرق تحليل متعددة الحدود أكثر تعقيدًا، مثل خوارزمية LLL وطريقة كرونيكر وطريقة تراجر، والتي لم يتم شرحها هنا بسبب صعوبتها الرياضية.

تمارين محلولة على تحليل كثيرات الحدود

بمجرد الانتهاء من رؤية جميع أنواع تحليل كثيرات الحدود إلى العوامل، ننصحك بالتدرب على محاولة حل التمارين. ولهذا السبب قمنا بإعداد العديد من التمارين التي تم حلها خطوة بخطوة لتحليل كثيرات الحدود أدناه. وتذكر أنه إذا كان لديك أي أسئلة، يمكنك كتابتها في التعليقات وسوف نقوم بالرد عليها بسرعة.

التمرين 1

قم بإجراء تحليل الدرجة 3 التالية متعددة الحدود:

$P(x)=x^3-3x^2-6x+8$

انظر الحل

إنها كثيرة حدود كاملة ومرتبة من الدرجة الثالثة ومستقلة في النهاية. ولذلك، فإننا نطبق طريقة روفيني لتحديد جذور كثيرة الحدود:

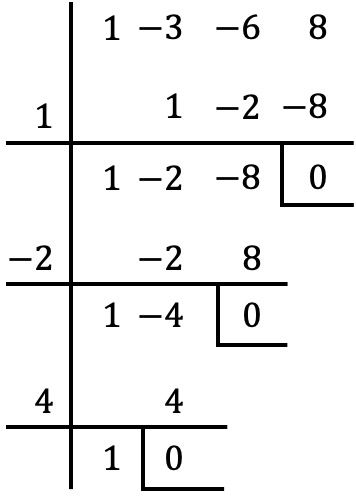
وبالتالي فإن جذور كثير الحدود هي كما يلي:

$x=+1 \qquad x=-2 \qquad x=+4$

وبالتالي فإن تحليل كثير الحدود هو:

$P(x)= 1 \cdot (x-1)\cdot (x+2) \cdot (x-4)$

$\bm{P(x)= (x-1)(x+2)(x-4)}$

تمرين 2

احسب تحليل الدرجة التالية متعددة الحدود من الدرجة 4:

$P(x)=x^4+x^3-7x^2-x+6$

انظر الحل

وهي كثيرة الحدود من الدرجة الرابعة ولها حد مستقل، لذلك نستخدم طريقة روفيني للعثور على جذور كثيرة الحدود:

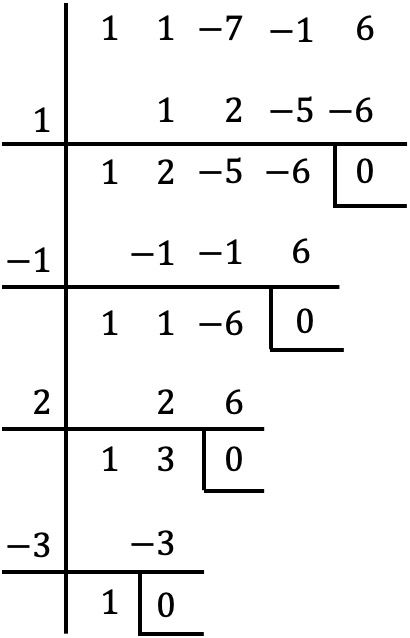
وبالتالي فإن جذور كثير الحدود هي:

$x=+1 \qquad x=-1 \qquad x=2 \qquad x=-3$

وعندما نقوم بتحليل كثيرة الحدود، يتبقى لدينا:

$P(x)= 1 \cdot (x-1)\cdot (x+1)\cdot (x-2) \cdot (x+3)$

$\bm{P(x)= (x-1)(x+1)(x-2)(x+3)}$

التمرين 3

أوجد تحليل كثيرة الحدود من الدرجة الرابعة التالية:

$P(x)=x^4-2x^3-13x^2-10x$

انظر الحل

في هذه الحالة ليس لكثيرة الحدود حد مستقل، يجب علينا أولاً استخراج عامل مشترك:

$P(x)=x(x^3-2x^2-13x-10)$

الآن بعد أن أخذنا العامل المشترك x، نحسب جذور أو أصفار كثيرة الحدود بين قوسين باستخدام طريقة روفيني:

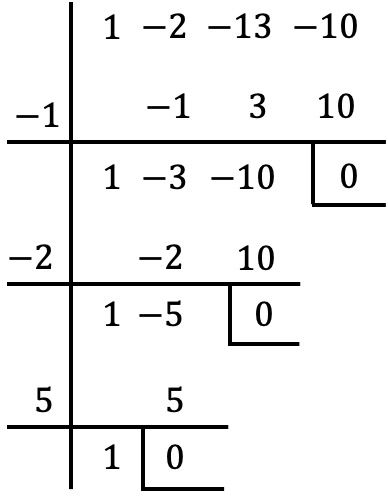
وبالتالي فإن جذور كثيرة الحدود هي تلك التي وجدناها بطريقة روفيني بالإضافة إلى x=0 للعامل المشترك:

$x=0 \qquad x=-1 \qquad x=-2 \qquad x=5$

وأخيرًا، بتحليل كثير الحدود إلى عوامل نحصل على التعبير التالي:

$P(x)= 1 \cdot x \cdot (x+1)\cdot (x+2)\cdot (x-5)$

$\bm{P(x)= x(x+1)(x+2)(x-5)}$

التمرين 4

حول كثيرة الحدود من الدرجة الثالثة التالية إلى عوامل:

$P(x)=6x^3+25x^2+21x-10$

انظر الحل

هذا كثير الحدود له مصطلح مستقل، لذلك نحسب جذوره باستخدام خوارزمية روفيني:

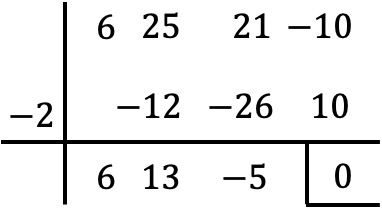
متعددات الحدود المضروب من الدرجة 3 في السطر 2

ومع ذلك، عندما نصل إلى هذه النقطة، لا يمكننا الاستمرار في تطبيق قاعدة روفيني، لأنه بدون عدد صحيح آخر، يكون باقي القسمة صفرًا.

ولذلك، فإننا نجعل كثيرة الحدود الناتجة تساوي الصفر:

$6x^2+13x-5=0$

ونطبق صيغة المعادلات التربيعية لحل المعادلة الناتجة:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-13 \pm \sqrt{13^2-4\cdot 6\cdot (-5)}}{2\cdot 6}= \cfrac{-13\pm \sqrt{169+120}}{12} = \cfrac{-13 \pm\sqrt{289}}{12}$

$\displaystyle x = \cfrac{-13 \pm 17}{12} = \begin{cases} \cfrac{-13+17}{12} = \cfrac{4}{12} = \cfrac{1}{3} \\[4ex]\cfrac{-13-17}{12} = \cfrac{-30}{12} = -\cfrac{5}{2} \end{cases}$

وبالتالي فإن جذور أو أصفار كثير الحدود هي:

$x=-2 \qquad x=\cfrac{1}{3} \qquad x=-\cfrac{5}{2}$

لذلك يجب أن يتم تحليل كثير الحدود إلى عوامل:

$\displaystyle P(x)= 6\left(x+2\right)\left(x-\frac{1}{3}\right)\left(x+\frac{5}{2}\right)$

التمرين 5

حدد تحليل الدرجة التالية متعددة الحدود من الدرجة 6:

$P(x)=x^6-3x^5+14x^3-12x^2$

انظر الحل

كثيرة الحدود في المشكلة ليس لها حد مستقل، لذلك يجب علينا أولا استخراج العامل المشترك، وهو في هذه الحالة

$x^2:$

$P(x)=x^2(x^4-3x^3+14x-12)$

وبمجرد إزالة العامل المشترك من كثيرة الحدود، نجد جذور كثيرة الحدود بين قوسين باستخدام قاعدة روفيني:

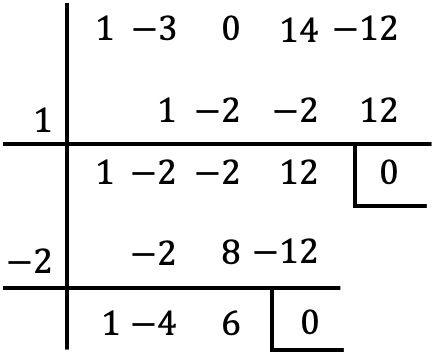
لكن عندما نصل إلى هذه المرحلة، لا يمكننا الاستمرار في المضي قدمًا، لأنه بدون عدد صحيح آخر، يكون الباقي صفرًا.

لذلك قمنا بتعيين كثير الحدود الذي تم الحصول عليه يساوي الصفر:

$x^2-4x+6=0$

ونحل المعادلة التربيعية بالصيغة:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1\cdot 6}}{2\cdot 1}= \cfrac{4\pm \sqrt{16-24}}{2} = \cfrac{4 \pm\sqrt{-8}}{2} \ \color{red} \bm{\times}$

لا توجد جذور للأعداد السالبة، لذا فإن المعادلة ليس لها حل، مما يعني أننا لا نستطيع العثور على المزيد من جذور كثيرة الحدود. وبعبارة أخرى، فإن كثيرة الحدود ليست قابلة للتحليل بشكل كامل.

ومع ذلك، فإن الجذور التي تمكنا من العثور عليها هي:

$x=0 \qquad x=0 \qquad x=1 \qquad x=-2$

لاحظ أن الجذر

$x=0$

يتكرر مرتين لأننا أزلنا العامل المشترك منه

$x^2,$

وبما أنه مربع، فهذا يعني أنه جذر مزدوج.

في الختام، فإن كثيرة الحدود المحللة ستكون حاصل ضرب جميع الجذور الموجودة معبرًا عنها كعوامل

$(x-a)$

مضروبًا في كثير الحدود الذي تم الحصول عليه من قاعدة روفيني والذي لا يمكن أخذه في الاعتبار:

$P(x)= 1 \cdot x^2 \cdot (x-1)\cdot (x+2)\cdot (x^2-4x+6)$

$\bm{P(x)= x^2(x-1)(x+2)(x^2-4x+6)}$

التمرين 6

قم بإجراء التحليلات لجميع كثيرات الحدود التالية:

$\text{A)} \ P(x)=x^2 + 12x+36$

$\text{B)} \ Q(x)=x^2 -64$

$\text{C)} \ R(x)=x^2 - 18x+81$

$\text{D)} \ S(x)=x^2+10x+24$

انظر الحل

متعدد الحدود في القسم أ) يتوافق مع هوية بارزة، ولا سيما مربع المجموع. وبالتالي فإن تحليلها هو:

$P(x)=x^2 + 12x+36 = \bm{(x+6)^2}$

تعد كثيرة الحدود في القسم B) أيضًا منتجًا ملحوظًا، ولا سيما الفرق بين المربعات، وبالتالي:

$Q(x)=x^2 -64 = \bm{(x+8)(x-8)}$

وبالمثل، فإن كثيرة الحدود في القسم ج) هي مساواة ملحوظة، ولا سيما أنها تتكون من مربع الطرح. وبالتالي فإن تحليلها هو:

$R(x)=x^2 - 18x+81 = \bm{(x-9)^2}$

وأخيرًا، فإن كثيرة الحدود في الجزء د) ليست هوية بارزة. لذلك يجب علينا أن نجعل كثيرة الحدود تساوي 0 ونحل المعادلة الناتجة للعثور على جذورها:

$x^2+10x+24 =0$

نستخدم صيغة المعادلة التربيعية:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-10 \pm \sqrt{10^2-4\cdot 1\cdot 24}}{2\cdot 1}= \cfrac{-10\pm \sqrt{100-96}}{2} = \cfrac{-10 \pm\sqrt{4}}{2}$

$\displaystyle x = \cfrac{-10 \pm 2}{2} = \begin{cases} \cfrac{-10+2}{2} = \cfrac{-8}{2} = -4 \\[4ex]\cfrac{-10-2}{2} = \cfrac{-12}{2} = -6\end{cases}$

وبالتالي فإن جذور كثيرة الحدود D) هي:

$x=-4 \qquad x=-6$

وأخيرًا، نتيجة تحليل كثيرات الحدود هي:

$\bm{S(x)=(x+4)(x+6)}$

ما هو التحليل متعدد الحدود؟

كيفية تحليل كثيرات الحدود إلى عوامل مع قاعدة روفيني

تحليل كثيرات الحدود بدون حد مستقل

تحليل كثيرات الحدود ذات الجذور العقلانية

حالات خاصة من العوملة كثيرات الحدود

تحليل الهويات البارزة

فرق المربعات

مربع الجمع والطرح

تحليل ثلاثيات الحدود من الدرجة الثانية

تحليل ثلاثية الحدود من الدرجة الرابعة مع الأسس الزوجية

تحليل كثيرات الحدود عن طريق التجميع

تمارين محلولة على تحليل كثيرات الحدود

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

التمرين 6

اترك تعليقاً إلغاء الرد