كيفية حساب جذور كثير الحدود؟ (تمارين محلولة)

في هذه الصفحة سوف تكتشف ما هي جذور كثيرة الحدود وكيفية حسابها. بالإضافة إلى ذلك، ستتمكن من رؤية أمثلة وتمارين تم حلها خطوة بخطوة على جذور كثيرة الحدود.

ما هي جذور كثير الحدود؟

في الرياضيات، جذور (أو أصفار) كثير الحدود هي القيم التي تلغي كثير الحدود. أي أن جذور كثير الحدود هي كل تلك القيم التي، عند تقييمها في كثير الحدود، لها قيمة عددية تساوي 0.

مؤخراً،

$x=a$

هو جذر كثير الحدود

$P(x)$

نعم

$P(a)=0.$

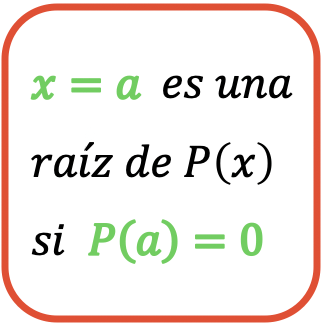
على سبيل المثال، إذا كان لدينا متعدد الحدود التالي:

$P(x)=x^2-3x+2$

يمكننا التحقق من أن أحد جذور كثيرة الحدود هو 1، حيث أن القيمة العددية لكثيرة الحدود عند x=1 تساوي صفر:

$P(1)=1^2-3\cdot 1+2 = 1-3+2 \color{blue} \bm{= 0}$

من ناحية أخرى، 3 ليس جذرًا لكثيرة الحدود لأنها ليست قيمة تلغي كثيرة الحدود، أو بمعنى آخر، القيمة العددية لكثيرة الحدود عند x=3 تختلف عن الصفر:

$P(3)=3^2-3\cdot 3+2 = 9-9+2=2 \color{blue} \bm{\neq 0}$

من المحتمل أنك تفهم الآن بشكل أفضل ما هو جذر كثيرة الحدود، لكن ألا ترغب في معرفة عدد جذور كثيرة الحدود؟ أو كيفية العثور على جميع جذور كثيرة الحدود؟ حسنًا، هذا بالضبط ما سنراه في القسم التالي.

كيفية حساب جميع جذور كثير الحدود؟

للعثور على جميع جذور كثيرة الحدود، يجب عليك اتباع الخطوات التالية:

أولاً، يتم حساب جميع مقسومات الحد المستقل لكثيرة الحدود.
ثانيا، يتم تقييم جميع القيم الموجودة في الخطوة السابقة في كثير الحدود.
أخيرًا، إذا كانت قيمته العددية تساوي صفرًا عند تقييم رقم في كثيرة الحدود، فإن الرقم المذكور هو جذر لكثيرة الحدود. وبخلاف ذلك، فإن الرقم المذكور لا يتوافق مع جذر كثيرة الحدود.

يتم استنتاج هذا الإجراء من نظرية الباقي ، انقر فوق هذا الرابط لمعرفة سبب هذا الإجراء بالذات.

مثال لحساب جذور كثيرة الحدود

سنحل أدناه مثالًا خطوة بخطوة حتى تتمكن من فهم كيفية الحصول على جذور كثيرة الحدود بشكل أفضل.

ما هي جميع جذور كثيرة الحدود التالية؟

$P(x) = x^2-5x+6$

أولًا، يجب علينا إيجاد قواسم الحد المستقل، لأن كل جذر لكثيرة الحدود هو أيضًا مقسوم على الحد المستقل. إذن قواسم العدد 6 هي:

قواسم العدد 6: +1، -1، +2، -2، +3، -3

تذكر أنه إذا كان الرقم مقسومًا عليه، فإن سالبه هو أيضًا مقسوم عليه. بما أن العدد يقبل القسمة على أعداد موجبة وسالبة.

وبالتالي، فإن الجذور أو الأصفار المحتملة لكثيرة الحدود هي: ±1، ±2، ±3. ولذلك، علينا تحديد القيمة العددية لكثيرة الحدود لجميع هذه القيم. وللقيام بذلك، نقوم باستبدال هذه القيم في تعبير كثيرة الحدود حيث يوجد x:

$P(1) = 1^2 -5\cdot 1 +6= 1 -5 +6 =2$

$P(-1) = (-1)^2 -5\cdot (-1) +6 =1+5+6 = 12$

$P(2) = 2^2 -5\cdot 2 +6 =4-10+6= \color{blue} \bm{0}$

$P(-2) = (-2)^2 -5\cdot (-2) +6 =4+10+6 =20$

$P(3) = 3^2 -5\cdot 3 +6 =9-15+6=\color{blue} \bm{0}$

$P(-3) = (-3)^2 -5\cdot (-3) +6 =9+15+6 =30$

لذا فإن كثيرة الحدود تختفي فقط عندما يكون المتغير x هو +2 أو +3، لذا فإليك جذور كثيرة الحدود:

جذور أو أصفار كثيرة الحدود : +2 و +3

من ناحية أخرى، لاحظ أن كثيرة الحدود لها عدد من الجذور مثل درجتها، أي أنه بما أن كثيرة الحدود من الدرجة الثانية، فهي لها جذرين. في خصائص جذور كثيرة الحدود (أدناه)، سنرى لماذا تنطبق هذه الخاصية دائمًا على أي كثيرة الحدود.

لقد رأينا للتو طريقة لإيجاد جذور كثيرة الحدود. ومع ذلك، لا تزال هناك طرق أخرى لتحقيق ذلك، على سبيل المثال يمكنك أيضًا العثور على جذور كثيرة الحدود باستخدام قاعدة روفيني. انقر على الرابط التالي لرؤية أمثلة على قاعدة روفيني ، وهنا سوف تكتشف مما تتكون هذه الطريقة المعروفة، وأيضا ما هي الاختلافات بين الإجراءين.

خصائص جذور كثير الحدود

جذور أو أصفار كثيرة الحدود لها الخصائص التالية:

كما رأينا سابقًا، فإن الجذور الصحيحة (أو الأصفار) لكثيرة الحدود هي قواسم الحد المستقل لكثيرة الحدود.

إذا كنا نعرف جميع جذور كثيرة الحدود، فيمكننا التعبير عن كثيرة الحدود المذكورة في صورة منتجات ذات الحدين من النوع
$(x-a).$

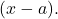
على سبيل المثال، كثير الحدود

$P(x) =x^3+3x^2-x-3$

لها 3 جذور وهي

$x=+1, x=-1$

$x=-3.$

يمكننا بالتالي إعادة كتابة كثيرة الحدود في صورة 3 مضاعفات للعوامل، كل منها يتكون من المتغير

$x$

وعلامة تغير الجذر:

$\displaystyle\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60} P(x) =x^3+3x^2-x-3 \ \longrightarrow \ \text{ra\'ices} \begin{cases} x=\color{verd}\bm{+1} \\[2ex] x=\color{vermell}\bm{-1} \\[2ex] x=\color{blau}\bm{-3}\end{cases}$

$\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60}P(x) =x^3+3x^2-x-3 = (x\color{verd}\bm{-1}\color{black})\cdot (x\color{vermell}\bm{+1}\color{black}) \cdot (x\color{blau}\bm{+3}\color{black})$

وهذا ما يسمى التخصيم متعدد الحدود. في الواقع، أحد التطبيقات الرئيسية لتحديد جذور كثيرة الحدود هو استخدامها لتحليلها. في الرابط التالي، يمكنك معرفة مم تتكون هذه العملية الخاصة جدًا، وبالإضافة إلى ذلك، يمكنك التدرب على حل تمارين تحليل كثيرات الحدود .

كثير الحدود له العديد من الجذور كما تشير درجته. لذلك، كثيرة الحدود من الدرجة الثانية سيكون لها جذرين، وكثيرة الحدود من الدرجة الثالثة سيكون لها 3 جذور، وكثيرة الحدود من الدرجة الرابعة سيكون لها 4 جذور، وهكذا.

إذا لم يكن لدى كثيرة الحدود حد مستقل، فهذا يعني أن أحد جذورها هو 0. ثم يجب أن تكون بقية الجذور مقسومة على معامل أحادية الحد من الدرجة الأدنى.

على سبيل المثال، كثير الحدود التالي ليس له مصطلح مستقل:

$P(x) =x^3+x^2-2x$

إذن، يجب بالضرورة أن يكون أحد جذر كثيرة الحدود 0. وبقية الجذور هي قواسم لمعامل الحد الأدنى من الدرجة، أي -2. بتعبير أدق، الجذور الأخرى هي

$x=+1$

$x=-2,$

إذن جميع جذور كثيرة الحدود هي:

جذور أو أصفار كثيرة الحدود: 0، +1 و -2

عندما لا يمكن تحديد جذور كثيرة الحدود، يقال أنها كثيرة الحدود غير قابلة للاختزال.

على سبيل المثال، سنحاول حساب جذور كثيرة الحدود التالية:

$P(x) =x^2+3x-1$

الجذور الوحيدة الممكنة لكثيرة الحدود هي قواسم -1، أي -1 و+1. لذلك نقوم بتقييم كثير الحدود لهذه القيم:

$P(1) = 1^2 +3\cdot 1 -1= 1 +3 -1 =3 \neq 0$

$P(-1) = (-1)^2 +3\cdot (-1)-1 =1-3-1 =-3 \neq 0$

لا يتم إلغاء كثيرة الحدود بأي حال من الأحوال، لذلك ليس لها جذور، وبالتالي فهي كثيرة الحدود غير قابلة للاختزال.

عندما يتكون كثير الحدود من حاصل ضرب عدة كثيرات الحدود، فليس من الضروري إجراء هذا الضرب لحساب الجذور، ولكن جذور كثيرة الحدود هي جذور كل عامل مضروبًا.

على سبيل المثال، إذا كان لدينا متعدد الحدود التالي:

$P(x) = (x-2) \cdot (x+1)$

من الخاصية الثانية لجذور كثيرات الحدود، يمكننا أن نستنتج أن جذر كثيرة الحدود اليسرى هو +2 وجذر كثيرة الحدود اليمنى هو -1.

$\displaystyle (x-2) \ \longrightarrow \ \text{ra\'iz} \ x=+2$

$\displaystyle (x+1) \ \longrightarrow \ \text{ra\'iz} \ x=-1$

وبالتالي، فإن جذور كثيرة الحدود الناتجة عن ضرب العاملين هي جذور كل منهما، أي +2 و -1.

$\displaystyle P(x) = (x-2) \cdot (x+1) \ \longrightarrow \ \text{ra\'ices} \ \begin{cases}x=+2 \\[2ex] x=-1 \end{cases}$

تمارين محلولة على جذور كثيرات الحدود

التمرين 1

تحديد ما إذا كان

$x = -4$

هو جذر كثير الحدود التالي:

$P(x)=x^3+2x^2-11x-12$

انظر الحل

لمعرفة ما إذا

$x=-4$

هو جذر كثيرة الحدود، ونحن بحاجة إلى تقييمه لتلك القيمة. حتى الآن:

$\begin{aligned}P(-4)& =(-4)^3+2\cdot (-4)^2-11\cdot (-4) -12 \\[2ex] & = -64+2\cdot 16 +44 -12 \\[2ex] & = -64+32+44 -12 \\[2ex] & = 0 \end{aligned}$

القيمة العددية لكثيرة الحدود في

$x=-4$

يساوي صفرًا، لذا فهو في الواقع جذر لكثيرة الحدود.

تمرين 2

احسب جميع جذور كثيرة الحدود التالية:

$P(x)=x^2-3x+2$

انظر الحل

أولًا، لإيجاد الجذور المحتملة لكثيرة الحدود، علينا إيجاد قواسم الحد المستقل. إذن قواسم العدد 2 هي:

قواسم العدد 2: +1، -1، +2، -2

وبالتالي فإن الجذور أو الأصفار المحتملة لكثيرة الحدود هي ±1 و±2. لذلك، نحن بحاجة إلى حساب مقدار كثيرة الحدود في كل هذه القيم:

$P(1)=1^2-3\cdot 1+2 =1-3+2=0$

$P(-1)=(-1)^2-3\cdot (-1)+2 =1+3+2=6$

$P(2)=2^2-3\cdot 2+2 =4-6+2=0$

$P(-2)=(-2)^2-3\cdot (-2)+2 =4+6+2=12$

وبالتالي، فإن كثيرة الحدود تختفي عندما تكون x +1 أو +2، لذا فإليك جذور كثيرة الحدود:

جذور أو أصفار كثيرة الحدود : +1 و +2

التمرين 3

أوجد جذور كثيرة الحدود التالية:

$P(x)=x^3-x^2-4x+4$

انظر الحل

يجب علينا أولًا إيجاد قواسم الحد المستقل، لأن جذر كثيرة الحدود هو أيضًا مقسوم على الحد المستقل. إذن قواسم العدد 4 هي:

قواسم العدد 4: +1، -1، +2، -2، +4، -4

وبالتالي فإن الجذور أو الأصفار المحتملة لكثيرة الحدود هي ±1 و±2 و±4. لذلك يجب علينا إيجاد القيمة العددية لكثيرة الحدود في كل هذه القيم:

$P(1)=1^3-1^2-4\cdot 1+4 =1-1-4+4=0$

$P(-1)=(-1)^3-(-1)^2-4\cdot (-1)+4 =-1-1+4+4=6$

$P(2)=2^3-2^2-4\cdot 2+4 =8-4-8+4=0$

$P(-2)=(-2)^3-(-2)^2-4\cdot (-2)+4 =-8-4+8+4=0$

$P(3)=3^3-3^2-4\cdot 3+4 =27-9-12+4=10$

$P(-3)=(-3)^3-(-3)^2-4\cdot (-3)+4 =-27-9+12+4=20$

وبالتالي، فإن كثيرة الحدود تختفي فقط عندما تكون x +1 أو +2 أو -2، لذا فإليك جذور كثيرة الحدود:

جذور أو أصفار كثيرة الحدود : +1، +2 و -2

التمرين 4

أوجد جذور كثيرة الحدود التالية:

$P(x)=x^3-6x^2+8x$

انظر الحل

في هذه الحالة، كثير الحدود ليس له حد مستقل. لذلك، وفقًا للخاصية الرابعة للجذور الموضحة أعلاه، نعلم أن أحد جذور كثيرة الحدود يجب أن يكون 0.

جذور كثيرة الحدود:

$x=0$

علاوة على ذلك، في هذه الحالة، الجذور المحتملة ليست قواسم الحد المستقل، بل هي قواسم معامل الحد الأدنى درجة، أي 8:

قواسم العدد 8: +1، -1، +2، -2، +4، -4، +8، -8

لذا فإن الجذور أو الأصفار المحتملة لكثيرة الحدود هي ±1، ±2، ±4 و±8. لذلك يجب علينا حساب القيمة العددية لكثيرة الحدود في جميع هذه القيم:

$P(1)=1^3-6\cdot 1^2+8\cdot 1 = 1-6+8=3$

$P(-1)=(-1)^3-6\cdot (-1)^2+8\cdot (-1) = -1-6-8=-15$

$P(2)=2^3-6\cdot 2^2+8\cdot 2 = 8-24+16=0$

$P(-2)=(-2)^3-6\cdot (-2)^2+8\cdot (-2) = -8-24-16=-48$

$P(4)=4^3-6\cdot 4^2+8\cdot 4 = 64-96+32=0$

$P(-4)=(-4)^3-6\cdot (-4)^2+8\cdot (-4) = -64-96-32=-192$

$P(8)=8^3-6\cdot 8^2+8\cdot 8 = 512-384+64=192$

$P(-8)=(-8)^3-6\cdot (-8)^2+8\cdot (-8) = -512-384-64=-960$

إذن يختفي كثير الحدود عندما تكون x +2 أو +4، وبالتالي فإن هذه القيم هي جذور كثير الحدود. ومع ذلك، نحتاج أيضًا إلى إضافة الجذر 0 الذي وجدناه في بداية المشكلة. في الختام، جميع جذور كثيرة الحدود هي:

جذور أو أصفار كثيرة الحدود : 0، +2 و +4

التمرين 5

استخدم خصائص جذور كثيرات الحدود لحساب جذور كثيرات الحدود التالية:

$P(x)=(x-1)(x+3)(x^2-x-2)$

انظر الحل

كما رأينا في الخاصية السادسة للجذور، عندما تتكون كثيرة الحدود من حاصل ضرب العوامل، ليس من الضروري حساب جميع الجذور، لأن جذور كثيرة الحدود بأكملها هي جذور كل عامل.

علاوة على ذلك، من الخاصية الثانية لجذور كثيرات الحدود، يمكننا أن نستنتج أن جذر العامل الأول هو +1 وجذر العامل الثاني هو -3.

$\displaystyle (x-1) \ \longrightarrow \ \text{ra\'iz} \ x=+1$