▷ كيفية قسمة كثيرات الحدود (تمارين محلولة)

في هذه الصفحة سوف تكتشف كيفية قسمة كثيرات الحدود، كل من تقسيم كثيرة الحدود على أحادية الحد وتقسيم كثيرة الحدود على كثيرة حدود أخرى. ستتمكن أيضًا من رؤية أمثلة على قسمة كثيرات الحدود والتدرب على حل التمارين خطوة بخطوة. وبالإضافة إلى ذلك، سوف تجد خصائص هذه العملية كثيرة الحدود.

تقسيم متعدد الحدود (أو متعدد الحدود).

قبل أن نرى بالضبط كيف يتم تقسيم كثيرات الحدود، سنراجع بإيجاز مفاهيم تقسيم كثيرات الحدود، بحيث يكون من الأسهل فهم الطريقة التي سنستخدمها.

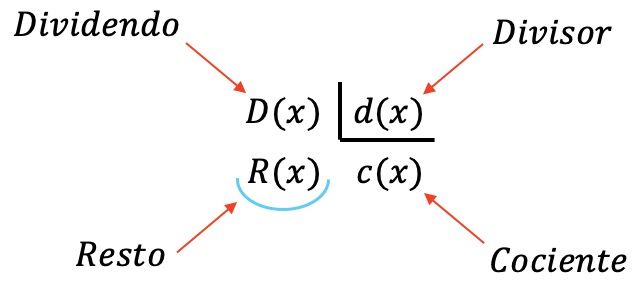
هناك أربعة كثيرات الحدود تشارك في تقسيم كثيرات الحدود:

توزيع الأرباح : كثير الحدود المقسمة.
المقسوم عليه : كثير الحدود الذي يقسم المقسوم.
حاصل القسمة : نتيجة قسمة المقسوم على المقسوم عليه.
الباقي (أو الباقي): كثير الحدود المتبقي عند القسمة بين كثيرتي الحدود.

ومن ناحية أخرى، يجب أن تعلم أيضًا أن هناك نوعين من التقسيم بين كثيرات الحدود:

التقسيم الدقيق لكثيرات الحدود : يكون التقسيم بين كثيرات الحدود دقيقًا عندما يكون الباقي صفرًا. في هذه الحالة، يكون توزيع كثير الحدود يساوي المقسوم عليه مضروبًا في حاصل القسمة.

$D(x)=d(x) \cdot c(x)$

علاوة على ذلك، في هذه الحالة، الأرباح

$D(x)$

هو مضاعف المقسوم عليه

$d(x)$

والحاصل

$c(x).$

وبالمثل، فإن مقسوم كثير الحدود وحاصل كثير الحدود كلاهما مقسوم على المقسوم.

التقسيم الصحيح لكثيرات الحدود : في التقسيم الصحيح (أو غير الدقيق) لكثيرات الحدود يكون الباقي غير صفر (0). ومن ثم يتم استيفاء الخاصية الأساسية لتقسيم كثيرات الحدود:

$D(x)=d(x) \cdot c(x) + R(x)$

الآن بعد أن رأينا ما هو قسمة كثيرات الحدود، دعونا نرى كيفية قسمة كثيرات الحدود على بعضها البعض. بتعبير أدق، سنشرح أولاً التقسيم بين كثيرة الحدود ووحيدة الحد ثم التقسيم بين كثيرتي الحدود.

تقسيم كثيرة الحدود بواسطة أحادية الحد

قبل أن نرى كيفية قسمة كثيرة الحدود على أحادية الحد، دعونا نتذكر أولاً كيفية تقسيم وحيدات الحد بينهما، لأنه من الضروري معرفة ذلك حتى نتمكن من القيام بهذا النوع من العمليات كثيرة الحدود.

قسمة وحدتين تتضمن قسمة معاملاتهما مع بعضهما البعض وأجزائهما الحرفية مع بعضهما البعض، أي أنه يتم تقسيم معاملات وحيدات الحد وطرح أسس المتغيرات التي لها نفس الأساس. ننظر إلى المثال التالي:

$12x^5: 3x^2 = \cfrac{12x^5}{3x^2}=(12:3) x^{5-2} = 4x^3$

الآن دعونا نرى ما يتضمنه تقسيم كثيرة الحدود على أحادية الحد:

في الرياضيات، لحل عملية تقسيم كثيرة الحدود على أحادية الحد، يتم قسمة كل حد من حدود كثيرة الحدود على أحادية الحد.

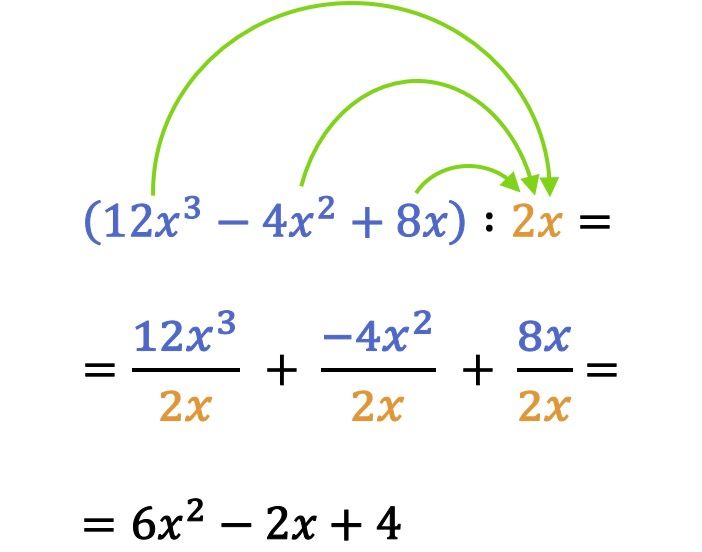
لاحظ في مثال القسمة السابق أنه عند قسمة أحاديات الحد أو متعددات الحدود، يجب عليك أيضًا مراعاة قاعدة العلامات. في الواقع، هناك خطأ شائع جدًا عند القسمة بين كثيرات الحدود ووحيدات الحد وهو الحصول على إشارة خاطئة للحد.

تقسيم كثيرة الحدود على كثيرة الحدود أخرى

لتقسيم كثيرات الحدود، تحتاج إلى اتباع إجراء ما، لذلك دعونا نرى كيف تبدو طريقة قسمة كثيرات الحدود، والتي تسمى أيضًا التقسيم الطويل لكثيرات الحدود، من خلال حل مثال خطوة بخطوة:

احسب نتيجة قسمة كثير الحدود
$P(x)$

بين كثير الحدود

$Q(x).$

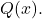
كونه متعدد الحدود اثنين:

$P(x) =x^3+4x^2+12 \qquad \qquad Q(x) =x-4$

$\cfrac{P(x)}{Q(x)} = \ ?$

أول شيء يجب فعله هو وضع كثيرات الحدود في صورة القسمة. على اليسار نكتب بسط الكسر (متعدد الحدود المقسوم عليه) وعلى اليمين نضع مقام الكسر (متعدد الحدود المقسوم عليه):

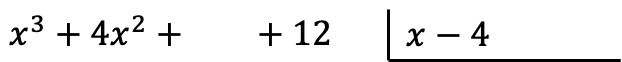
تحذير: إذا لم يكن لكثيرة الحدود أحادية الحد بدرجة معينة، فيجب أن نترك مسافة في مكانها. على سبيل المثال، كثير الحدود

$x^3+4x^2+12$

لا يوجد فصل دراسي في السنة الأولى، لذا توجد مساحة فارغة بدلاً من ذلك.

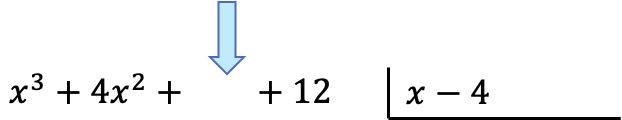
تقسيم كثيرات الحدود عندما يكون المصطلح مفقودًا

بمجرد أن نحصل على كثيرات الحدود في مكانها الصحيح، سنوجد حاصل القسمة. ولإيجاد الحد الأول من حاصل القسمة يجب علينا قسمة الحد الأول من المقسوم على الحد الأول من المقسوم عليه:

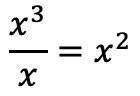
ونضع نتيجة القسمة مكان خارج القسمة:

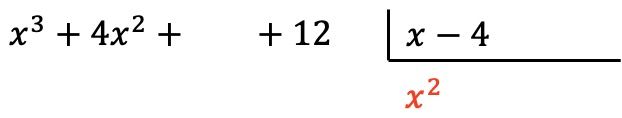
الآن نضرب الحد الذي وجده كل عنصر من عناصر المقسوم عليه، ونضع كل نتيجة أسفل المقسوم في العمود المقابل لها ، مع تغيير إشارتها :

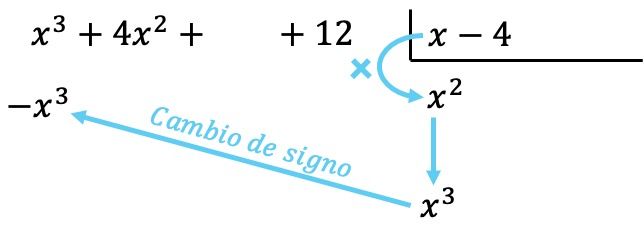
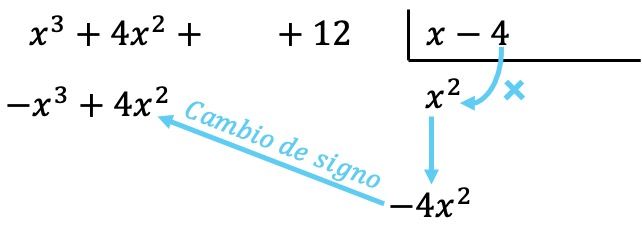
كما هو الحال في جميع العمليات مع كثيرات الحدود، من المهم ترتيب كثيرات الحدود من أعلى درجة إلى أدنى درجة بحيث تكون جميع الحدود من نفس الدرجة في نفس العمود.

بمجرد أن نضع نتائج الضرب مع الإشارة المعاكسة، نحتاج إلى إضافة الحدود المحاذاة رأسيًا:

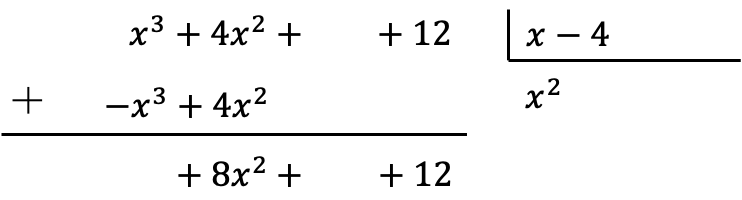
لاحظ أنه من خلال جمع هذا المبلغ، يلغي المعامل ذو الدرجة الأعلى، ومن ثم يصبح لدينا حد أقل في المقسوم.

نحتاج الآن إلى تكرار نفس الإجراء حتى يصبح مقسوم كثير الحدود أقل بدرجة واحدة من المقسوم عليه كثير الحدود.

لذلك نقسم الحد الأول من المقسوم على الحد الأول للمقسوم عليه:

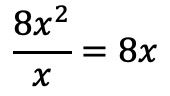
نضع النتيجة في الحاصل:

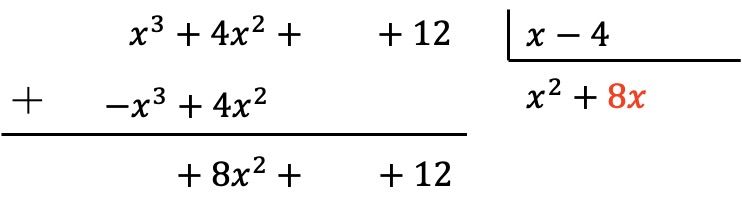
كما في السابق، نضرب الحد الجديد للناتج في كل عنصر من عناصر المقسوم عليه ونضع نتائج الإشارة المعاكسة في الأعمدة المقابلة للمقسوم:

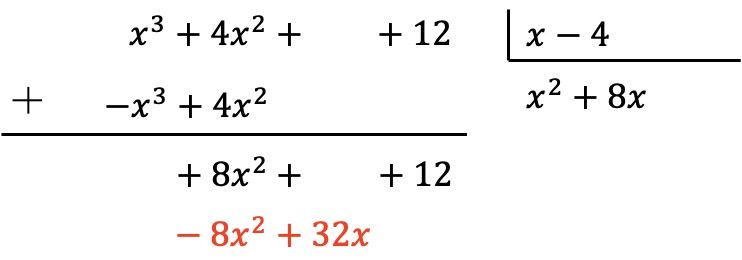
ونضيف عموديا:

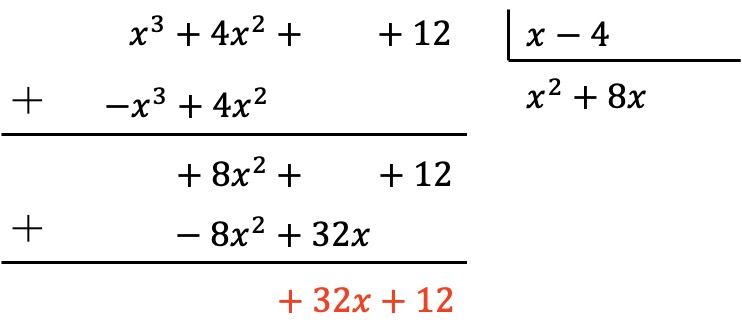
لا تزال كثيرة الحدود المقسوم عليها أقل بدرجة واحدة من كثيرة الحدود المقسوم عليها، لذا علينا الاستمرار في القيام بنفس العملية.

لذلك نقسم أولًا الحد الأول من المقسوم على الحد الأول للمقسوم عليه، ثم نضرب النتيجة في كل حد من المقسوم عليه، ثم نضع النتائج المعدلة في علامة المقسوم، وأخيرًا نضيف رأسيًا:

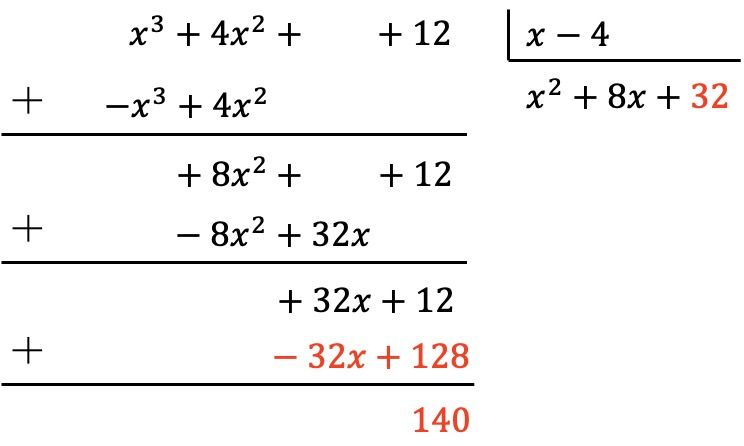
لقد حصلنا بالفعل على أن كثيرة حدود المقسوم هي درجة أقل من درجة المقسوم عليه، لأن المقسوم هو من الدرجة 0 والمقسوم عليه من الدرجة 1. وبالتالي، اكتملت القسمة.

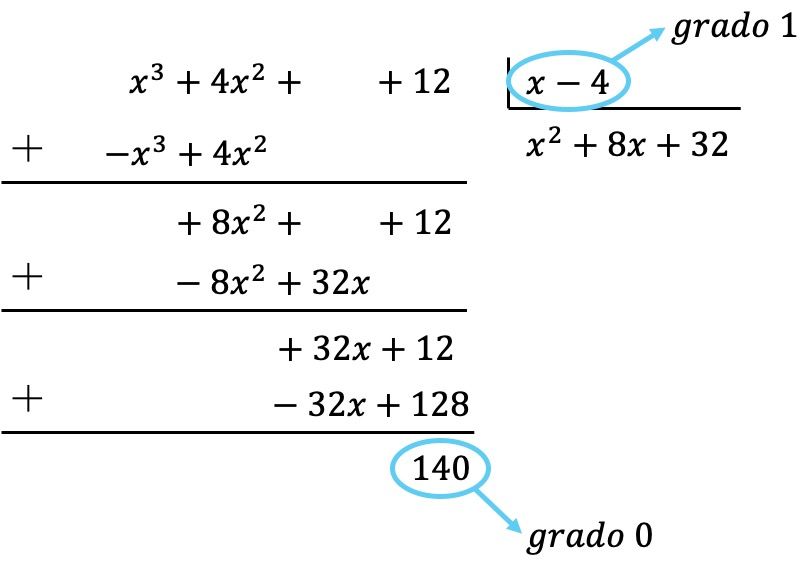
وبالتالي فإن نتيجة التقسيم هي:

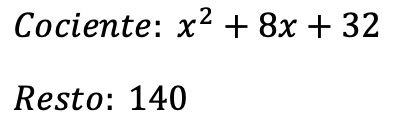
ومن ناحية أخرى، يمكننا التحقق من أننا قمنا بتقسيم كثيرات الحدود بشكل صحيح بناءً على الشرط الأساسي لتقسيم كثيرات الحدود:

$D(x)=d(x) \cdot c(x) + R(x)$

$x^3+4x^2+12=(x-4) \cdot (x^2+8x+32) + 140$

$x^3+4x^2+12=x^3+8x^2+32x-4x^2-32x-128+ 140$

$x^3+4x^2+12=x^3+4x^2+12$

✅

لقد تم استيفاء المعادلة، وبالتالي تم إجراء قسمة كثيرات الحدود بشكل صحيح.

وبهذا نكون قد انتهينا من قسمة كثيرات الحدود، نأمل أن نكون قد استطعنا مساعدتك في هذا الشرح. ما رأيك في طريقة تقسيم كثيرات الحدود؟ هل لديك شك؟ هل أحببت ذلك؟ أو هل تفضل عدم وجود تقسيمات متعددة الحدود؟ 😂 نقرأ لك في التعليقات! 👇👇👇

خصائص تقسيم كثيرات الحدود

أي تقسيم لكثيرات الحدود يتوافر فيه الخصائص التالية:

✓ يجب أن تكون درجة مقسوم كثير الحدود دائمًا أكبر من درجة المقسوم عليه.

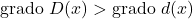$\text{grado } D(x) >\text{grado } d(x)” title=”Rendered by QuickLaTeX.com” height=”19″ width=”193″ style=”vertical-align: -5px;”></p> </p> <p style=$ ✓ درجة مقسوم كثير الحدود تعادل مجموع درجات المقسوم عليه وحاصل القسمة.

$\text{grado } D(x) =\text{grado } d(x)+\text{grado } c(x)$

✓ درجة الباقي تكون دائمًا أقل من درجة المقسوم عليه (وبالتالي أيضًا من المقسوم).

$\text{grado } R(x) <\text{grado } d(x)$

✓ المقسوم يساوي حاصل ضرب المقسوم عليه زائد الباقي. يتم وضع هذا الشرط أيضًا في قسمة الأرقام.

$D(x)=d(x) \cdot c(x) + R(x)$

تمارين محلولة على قسمة كثيرات الحدود

التمرين 1

حدد نتيجة التقسيم التالي لكثيرة الحدود على أحادية الحد:

$\left(15x^5+9x^3 \right) : \left(3x^2\right)$

انظر الحل

لتقسيم كثيرة الحدود على أحادية الحد، يجب عليك حل قسمة كل حد من كثيرة الحدود على أحادية الحد المذكورة:

$\begin{aligned} \left(15x^5+9x^3 \right) : \left(3x^2\right) & = \cfrac{15x^{5}}{3x^2}+ \cfrac{9x^3}{3x^2} \\[2ex] & = \bm{5x^3+3x} \end{aligned}$

تذكر أنه عند القسمة بين أحاديات الحد، يتم تقسيم المعاملات فيما بينها ويتم طرح أسس القوى التي لها نفس الأساس.

تمرين 2

احسب التقسيم التالي لكثيرة الحدود على أحادية الحد:

$\left( 16x^5-4x^3-20x^2 \right) : \left(4x^2\right)$

انظر الحل

لتقسيم كثيرة الحدود على أحادية الحد، يجب عليك قسمة كل حد من كثيرة الحدود على أحادية الحد المذكورة:

$\begin{aligned} \left( 16x^5-4x^3-20x^2 \right) : \left(4x^2\right) & = \cfrac{16x^5}{4x^2}+ \cfrac{-4x^3}{4x^2} + \cfrac{-20x^2}{4x^2} \\[2ex] & = \bm{4x^3-x-5} \end{aligned}$

تذكر أنه في قسمة أحادية الحد، يتم تقسيم المعاملات فيما بينها ويتم طرح أسس القوى ذات الأساس المكافئ.

التمرين 3

حل التقسيم التالي لكثيرة الحدود بواسطة أحادية الحد:

$\left(12x^{10}-30x^7-18x^6+54x^4 \right) : \left(-6x^3\right)$

انظر الحل

لتقسيم كثيرة الحدود على أحادية الحد، يجب عليك حل قسمة كل حد من كثيرة الحدود على أحادية الحد المذكورة:

$\begin{aligned} \left(12x^{10}-30x^7-18x^6+54x^4 \right) : \left(-6x^3\right) & = \cfrac{12x^{10}}{-6x^3}+ \cfrac{-30x^{7}}{-6x^3} + \cfrac{-18x^6}{-6x^3} + \cfrac{54x^4}{-6x^3} \\[2ex] & = \bm{-2x^7+5x^4+3x^3-9x} \end{aligned}$

ضع في اعتبارك أن أحادية الحد القسمة تكون سالبة وبالتالي تتغير علامات جميع الأقسام.

التمرين 4

قم بإجراء التقسيم التالي لكثيرات الحدود:

$\cfrac{x^4+x^3-x^2+x+1}{x^3-5}$

انظر الحل

لتقسيم كثيرات الحدود يجب عليك تطبيق الطريقة الموضحة أعلاه:

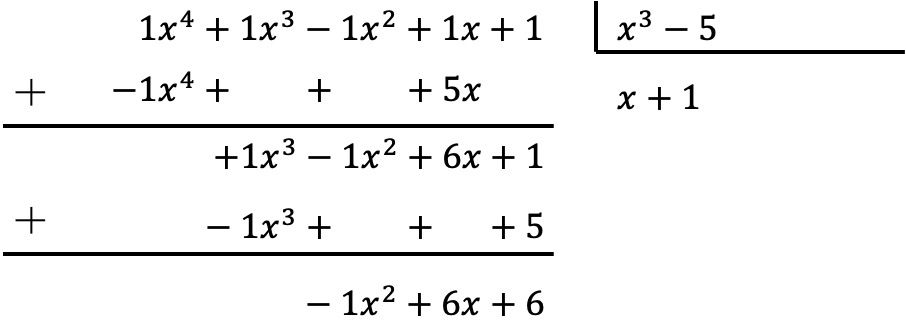
وبالتالي فإن نتيجة القسمة بين كثيرتي الحدود هي:

حاصل القسمة:

$x+1$

استراحة:

$-x^2+6x+6$

التمرين 5

احسب التقسيم التالي لكثيرات الحدود:

$\cfrac{2x^3-3x^2-5x-5}{x-2}$

انظر الحل

لحل قسمة كثيرة الحدود على ذات الحدين يجب علينا تطبيق الطريقة التي رأيناها أعلاه:

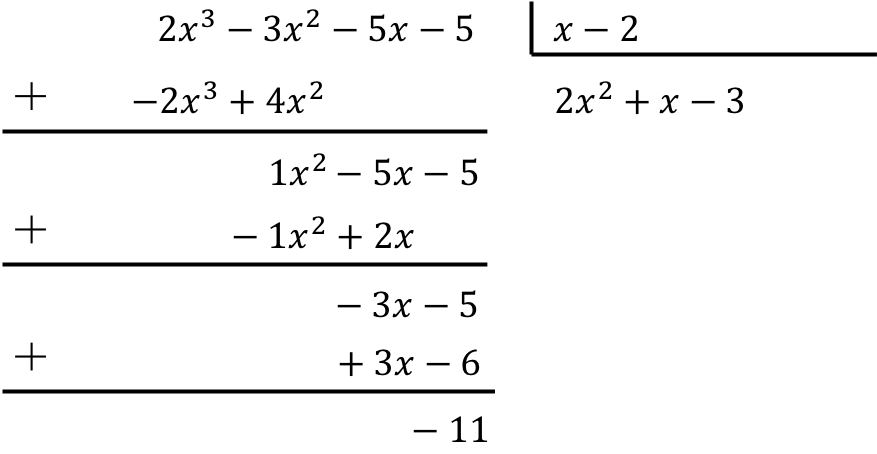
تمارين محلولة خطوة بخطوة لتقسيم كثيرات الحدود

وبالتالي فإن نتيجة تقسيم كثيرات الحدود هي:

حاصل القسمة:

$2x^2+x-3$

استراحة:

$-11$

التمرين 6

حل التقسيم التالي لكثيرات الحدود:

$\cfrac{x^4+x^2+3}{x^3+3x^2+2x}$

انظر الحل

لحساب تقسيم كثيرات الحدود يجب علينا تطبيق الطريقة الموضحة:

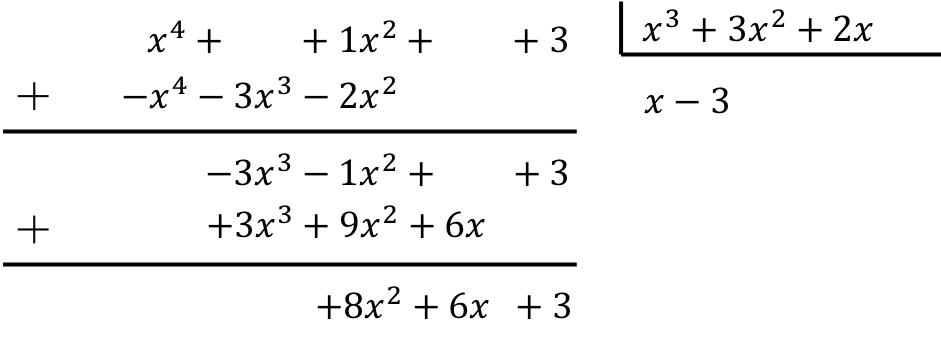
وبالتالي فإن نتيجة القسمة بين كثيرتي الحدود هي:

حاصل القسمة:

$x-3$

استراحة:

$8x^2+6x+3$

التمرين 7

أوجد نتيجة التقسيم التالي بين كثيرتي الحدود:

$\cfrac{x^4-2x^3+x^2-x-3}{x^2+x+1}$

انظر الحل

لحساب تقسيم كثير الحدود على ثلاثي الحدود يجب عليك تطبيق الطريقة الموضحة:

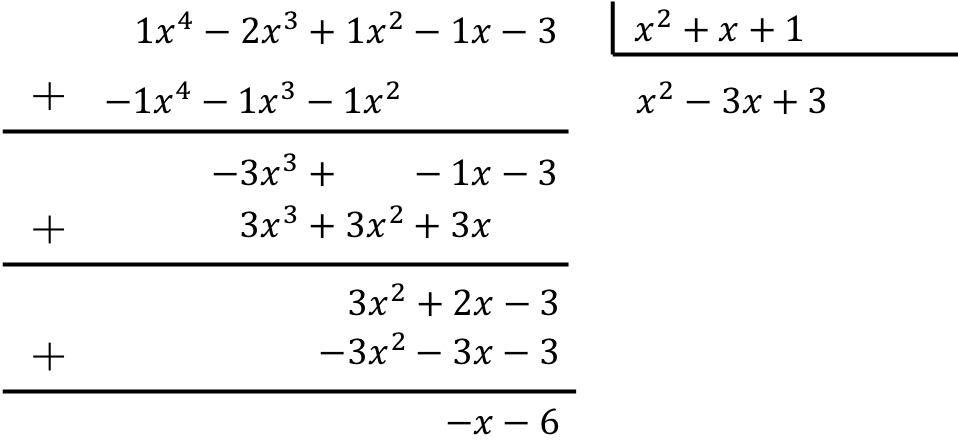
تمارين حلها خطوة بخطوة لتقسيم كثيرات الحدود

وبالتالي فإن نتيجة القسمة بين كثيرتي الحدود هي:

حاصل القسمة:

$x^2-3x+3$

استراحة:

$-x-6$

👉👉👉 إذا وصلت إلى هذا الحد، فهذا يعني أنك تعرف بالفعل كيفية تقسيم كثيرات الحدود. ساطع! الآن بعد أن أتقنت تقسيم كثيرات الحدود، اعلم أن هناك طريقة تسمح لك بحل عمليات تقسيم معينة بين كثيرات الحدود بسرعة أكبر . هذه قاعدة اصطناعية أو قاعدة روفيني ، يمكنك رؤية كيفية تطبيق هذه الخدعة ومتى يمكن استخدامها من خلال النقر على الرابط.😉

تقسيم متعدد الحدود (أو متعدد الحدود).

تقسيم كثيرة الحدود بواسطة أحادية الحد

تقسيم كثيرة الحدود على كثيرة الحدود أخرى

خصائص تقسيم كثيرات الحدود

تمارين محلولة على قسمة كثيرات الحدود

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

التمرين 6

التمرين 7

اترك تعليقاً إلغاء الرد