الحدود الجانبية

نوضح في هذه المقالة ما هو الحد الجانبي للدالة (مع الأمثلة). نحن نعلمك أيضًا كيفية حساب الحدود الجانبية اليسرى واليمنى للدالة، بيانيًا وعدديًا. بالإضافة إلى ذلك، ستتمكن من التدرب من خلال التمارين التي تم حلها خطوة بخطوة للحدود الجانبية.

ما هي الحدود الجانبية؟

الحدود الجانبية للدالة عند نقطة ما تدرس سلوك الوظيفة حول تلك النقطة. هناك الحد الجانبي الأيسر والحد الجانبي الأيمن، والذي يحلل قيمة الدالة إلى يسار ويمين النقطة المدروسة على التوالي.

الحدود الجانبية لليسار واليمين

وكما رأينا في تعريف الحدود الجانبية فإن هناك نوعين: الحدود الجانبية اليسرى والحدود الجانبية اليمنى.

يتم التعبير عن الحد الأيسر للدالة بعلامة الطرح عند النقطة التي يتم فيها تحليل النهاية، ومن ناحية أخرى، تتم الإشارة إلى الحد الأيمن بعلامة الزائد.

الحد الجانبي على اليسار

$\displaystyle\lim_{x\to a^{\color{orange}\bm{-}\color{black}}}f(x)$

الحد الجانبي على اليمين

$\displaystyle\lim_{x\to a^{\color{orange}\bm{+}\color{black}}}f(x)$

انظر إلى المثال التالي لفهم معنى الحدود الجانبية بشكل أفضل:

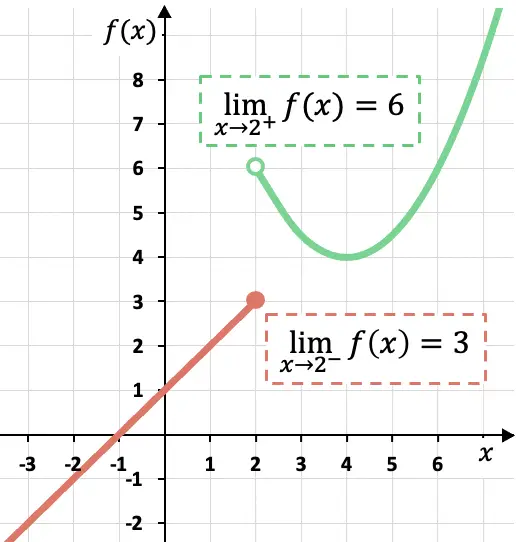
كما ترون في التمثيل البياني لهذه الدالة متعددة التعريف، فإن الحدود الجانبية تعتمد على الجانب الذي تم حسابها عليه.

في هذه الحالة، تقترب الدالة من 3 عندما يقترب x من 2 من اليسار، حيث أن الدالة تأخذ قيمًا أقرب إلى 3 عندما يقترب x من x=2 من يسارها.

ومن ناحية أخرى، فإن الحد الجانبي للدالة عند x=2 بالخط يساوي 6. لأننا إذا اقتربنا من النقطة x=2 بخطها، فإن الدالة تأخذ قيمًا أقرب فأقرب إلى f(x)= 6.

ومن ناحية أخرى، يجب أن تعلم أن النهايات الجانبية لها نفس خصائص النهايات العادية. في الرابط التالي يمكنك معرفة ما هي خصائص الحدود:

➤ انظر: خصائص الحدود

حدود جانبية متساوية

لقد رأينا للتو مثالاً حيث تكون الحدود الجانبية للدالة مختلفة، ولكن… ماذا يحدث إذا كانت الحدود الجانبية متماثلة؟

إذا كان كلا الحدين الجانبيين للدالة عند نقطة ما موجودين ومتساويين ، فإن نهاية الدالة موجودة عند تلك النقطة وتكون نتيجة النهاية هي قيمة النهايتين الجانبيتين.

بمعنى آخر، لكي تكون نهاية الدالة موجودة عند نقطة ما، يجب استيفاء الشرط التالي:

$\displaystyle\lim_{x\to a^-}f(x)=\lim_{x\to a^+}f(x)=L \ \iff \ \lim_{x\to a}f(x)=L$

ولذلك، إذا كانت الحدود الجانبية للدالة عند نقطة ما مختلفة، فإن نهاية الدالة عند تلك النقطة غير موجودة.

كما أن وجود نهاية الدالة عند نقطة ما هو شرط أساسي لتكون دالة متصلة عند نقطة ما .

لنحل مثالاً لنكمل فهم مفهوم النهايات الجانبية:

تتطابق الحدود الجانبية عند النقطة x=-2 للدالة الممثلة بيانيا، حيث أن قيمة الدالة تميل نحو 3 سواء اقتربنا من x=-2 من اليسار أو من اليمين. وبالتالي فإن نهاية الدالة عند x=-2 تساوي 3.

$\displaystyle\lim_{x\to -2^-}f(x)=\lim_{x\to -2^+}f(x)=3 \ \longrightarrow \ \lim_{x\to -2}f(x)=3$

من ناحية أخرى، عند النقطة x=4 تختلف الحدود الجانبية، حيث أن الدالة من اليسار تقترب من f(x)=3 ولكن من اليمين تقترب الدالة من f(x)=2. وبالتالي فإن نهاية الدالة عند هذه النقطة غير موجودة.

$\displaystyle\lim_{x\to 4^-}f(x)=3 \neq \lim_{x\to 4^+}f(x)=2 \ \longrightarrow \ \cancel{\exists} \ \lim_{x\to 4}f(x)$

حساب الحدود الجانبية

وبالنظر إلى تعريف الحدود الجانبية سنرى كيفية حسابها عدديا من خلال حل المثال التالي:

$\displaystyle\lim_{x\to 2}\frac{3}{x-2}$

إذا قمنا بحساب النهاية كالمعتاد، نحصل على عدم تعيين عدد حقيقي مقسومًا على 0:

$\displaystyle\lim_{x\to 2}\frac{3}{x-2}=\frac{3}{2-2}=\frac{3}{0}=\infty$

ومع ذلك، عند حساب الحدود الجانبية، لا نحصل على أي عدم تعيين.

$\displaystyle\lim_{x\to 2^-}\frac{3}{x-2}=\ \color{red}\bm{?}\color{black} \qquad \lim_{x\to 2^+}\frac{3}{x-2}=\ \color{red}\bm{?}$

لحساب الحد الجانبي للدالة من اليسار عند x=2، يجب أن تأخذ رقمًا أصغر من x=2 ولكنه قريب جدًا منه، على سبيل المثال x=1.999.

$\displaystyle\lim_{x\to 2^-}\frac{3}{x-2}=\frac{3}{\color{red}\bm{1,999}\color{black}-2}$

في هذه الحالة سيكون المقام رقمًا سالبًا بقيمة صغيرة جدًا ولكنها ليست حتى صفرًا، وعادةً ما يتم تمثيله بصفر وعلامة الطرح أمامه:

$\displaystyle\lim_{x\to 2^-}\frac{3}{x-2}=\frac{3}{1,999-2}=\frac{3}{\color{red}\bm{-0}\color{black}}$

ولذلك فإن نتيجة النهاية الجانبية هي ناقص ما لا نهاية، لأن أي عدد مقسوم على 0 يعطي ما لا نهاية، وموجب مقسوم على سالب يعطي سالب:

$\displaystyle\lim_{x\to 2^-}\frac{3}{x-2}=\frac{3}{1,999-2}=\frac{3}{-0}=\color{red}\bm{-\infty}\color{black}$

يمكننا التحقق من أن الدالة تقترب من ناقص اللانهاية عن طريق حساب صور الدالة بقيم أقرب إلى x=2 من اليسار.

$\begin{array}{c}\begin{array}{l}f(1,9)=\cfrac{3}{1,9-2}=-30\\[2ex]f(1,99)=\cfrac{3}{1,99-2}=-300\\[2ex]f(1,999)=\cfrac{3}{1,999-2}=-3000\\[2ex]f(1,9999)=\cfrac{3}{1,9999-2}=-30000\\[2ex]f(1,99999)=\cfrac{3}{1,99999-2}=-300000\end{array}\\[16ex]\vdots\\[1.5ex] f(2^-)=-\infty\end{array}$

وبالمثل، للعثور على نهاية الدالة عند النقطة x=2 على اليمين، يمكننا تطبيق نفس المنطق: نأخذ قيمة أكبر من 2 ولكنها قريبة جدًا، مثل 2001.

$\displaystyle\lim_{x\to 2^+}\frac{3}{x-2}=\frac{3}{2,001-2}=\frac{3}{+0}=+\infty$

وبنفس الطريقة يمكننا التحقق من أن الدالة تتجه نحو اللانهاية عن طريق حساب صور الدالة بقيم أقرب وأقرب إلى x=2 من اليمين.

$\begin{array}{c}\begin{array}{l}f(2,1)=\cfrac{3}{2,1-2}=30\\[2ex]f(2,01)=\cfrac{3}{2,01-2}=300\\[2ex]f(2,001)=\cfrac{3}{2,001-2}=3000\\[2ex]f(2,0001)=\cfrac{3}{2,0001-2}=30000\\[2ex]f(2,00001)=\cfrac{3}{2,00001-2}=300000\end{array}\\[16ex]\vdots\\[1.5ex] f(2^+)=+\infty\end{array}$

في الرسم البياني التالي يمكنك أن ترى تمثيل الوظيفة التي تم تحليلها. كما ترون، الحد الجانبي للدالة عند النقطة x=2 على اليسار هو سالب ما لا نهاية، والحد الجانبي للدالة عند النقطة x=2 على اليمين هو زائد ما لا نهاية.

تم إصلاح مشكلات الحدود الجانبية

التمرين 1

أوجد الحدود الجانبية للدالة المحددة متعددة التعريف التالية عند النقاط التي يتغير فيها التعريف (x=-2 وx=4).

انظر الحل

الحدود الجانبية لا تتطابق عند النقطة x=-2، على اليسار تتجه الدالة نحو f(x)=5، ومن ناحية أخرى، على اليمين تكون الدالة ثابتة وتساوي 3.

$\displaystyle\lim_{x\to -2^-}f(x)=5$

$\displaystyle\lim_{x\to -2^+}f(x)=3$

تختلف الحدود الجانبية أيضًا عندما تقترب x من 4. تقترب الدالة المتعددة التعريف من 3 من اليسار، ولكنها تقترب من -2 من اليمين.

$\displaystyle\lim_{x\to 4^-}f(x)=3$

$\displaystyle\lim_{x\to 4^+}f(x)=-2$

تمرين 2

حدد ما إذا كانت النهاية موجودة عندما تقترب x من 3 للدالة المتعددة التعريف التالية، وإذا كان الأمر كذلك، فما قيمتها.

انظر الحل

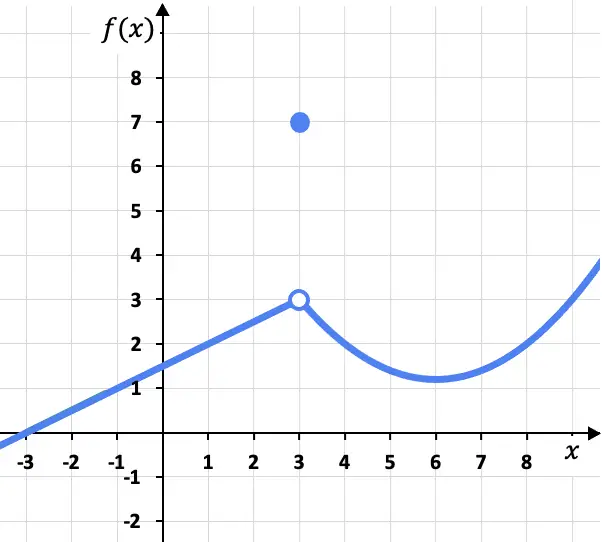
في هذه المشكلة تكون الحدود الجانبية عند النقطة x=3 من اليسار ومن اليمين متطابقة، حيث أن الدالة تميل نحو نفس القيمة (f(x)=3) سواء تم الاقتراب منها من اليسار أو من اليمين . جانبه الأيمن :

$\displaystyle\lim_{x\to 3^-}f(x)=3$

$\displaystyle\lim_{x\to 3^+}f(x)=3$

ولذلك، ووفقاً للتعريف الرياضي للنهاية، فإن نهاية الدالة عندما تميل x إلى 3 تساوي 3، لأن الحدين الجانبيين عند نفس النقطة يتطابقان عند هذه القيمة:

$\displaystyle\lim_{x\to 3^-}f(x)=\lim_{x\to 3^+}f(x)=3 \ \longrightarrow \ \lim_{x\to 3}f(x)=3$

على الرغم من أن نهاية الدالة عند x=3 هي 3، إلا أنه يجب الأخذ في الاعتبار أن الدالة عند هذه النقطة ليست 3، بل f(3)=7. وكما سنرى لاحقاً، فهذا يعني أن الدالة ليست متصلة عند x=3، بل لها انقطاع يمكن تجنبه.

التمرين 3

احسب الحدود الجانبية للدالة المنطقية التالية عند النقطة x=4.

$f(x)=\cfrac{-2x+3}{x-4}$

انظر الحل

لحساب النهاية عندما تتجه x نحو 4 من اليسار، نأخذ قيمة أقل من 4 ولكنها قريبة جدًا منها، على سبيل المثال 3,999:

$\displaystyle\lim_{x\to 4^-}\frac{-2x+3}{x-4}=\frac{-2\cdot 3,999+3}{3,999-4}=\frac{-4,998}{-0}=+\infty$

وبالتالي فإن الحد الجانبي عندما تقترب x من 4 من اليسار هو زائد ما لا نهاية.

ولحل النهاية عندما يميل x نحو 4 من اليمين، نقيم الدالة بقيمة أكبر من 4 ولكنها قريبة جدًا منها، على سبيل المثال 4,001:

$\displaystyle\lim_{x\to 4^+}\frac{-2x+3}{x-4}=\frac{-2\cdot 4,001+3}{4,001-4}=\frac{-5,002}{+0}=-\infty$

وبالتالي فإن الحد الجانبي عندما تقترب x من 4 من اليمين هو سالب ما لا نهاية.

التمرين 4

أوجد النهاية، إن وجدت، للدالة المتعددة التعريف التالية المعرفة عند النقطة x=2:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2-3 & \text{si} & x \leq 2 \\[2ex]\displaystyle \frac{-3x+5}{x-3} & \text{si} & x>2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”75″ width=”235″ style=”vertical-align: 0px;”></p> </p> <div class=$

انظر الحل

في هذه الحالة، يطلب منا بيان المشكلة إيجاد النهاية التي تغير فيها الدالة المتعددة التعريف التعبير، لذا علينا إيجاد النهاية على الجانب الأيسر باستخدام التعبير الأول والنهاية على الجانب الأيمن باستخدام التعبير الثاني.

$\displaystyle\lim_{x\to 2^+}f(x)=\lim_{x\to 2^+}\frac{-3x+5}{x-3}=\frac{-3\cdot 2+5}{2-3}=\frac{-1}{-1}=1$

نهاية الدالة عند x=2 على اليسار تتطابق مع نهاية الدالة على اليمين، وبالتالي فإن نهاية الدالة موجودة وتساوي 1:

$\displaystyle\lim_{x\to 2^-}f(x)=\lim_{x\to 2^+}f(x)=1 \ \longrightarrow \ \lim_{x\to 2}f(x)=1$

ما هي الحدود الجانبية؟

الحدود الجانبية لليسار واليمين

حدود جانبية متساوية

حساب الحدود الجانبية

تم إصلاح مشكلات الحدود الجانبية

التمرين 1

تمرين 2

التمرين 3

التمرين 4

اترك تعليقاً إلغاء الرد