▷ مشتق الطرح (الصيغة والتدريبات المحلولة)

نشرح في هذه المقالة كيفية استخلاص طرح الدوال (الصيغة). ستجد أيضًا أمثلة على مشتقات الطرح وتمارين تم حلها خطوة بخطوة للتدرب عليها.

صيغة مشتقة الطرح

مشتقة طرح دالتين تساوي طرح مشتقة كل دالة على حدة.

$z(x)=f(x)-g(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} z'(x)=f'(x)-g'(x)$

بمعنى آخر، اشتقاق دالتين منفصلتين ثم طرحهما يعادل طرح الدالتين أولًا ثم أخذ المشتقة.

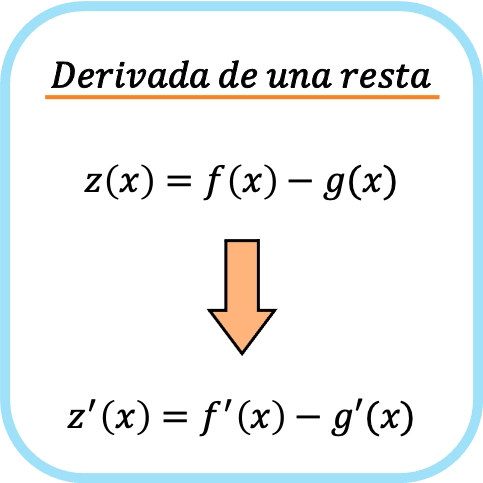
وبالمثل، تنطبق نفس قاعدة الاشتقاق على طرح دالتين أو أكثر، لذلك إذا كان لدينا طرح ثلاث، أربع، خمس،…، نحتاج إلى اشتقاق كل منها على حدة ثم طرحها.

$\begin{array}{c}z(x)=f(x)- g(x)- h(x)- \dots\\[1.5ex]\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex]z'(x)=f'(x)-g'(x)- h'(x)- \dots\end{array}$

كما ترون، فإن صيغة مشتقة اختلاف الدوال تشبه إلى حد كبير قاعدة مشتقة المجموع.

➤ انظر: مشتقة مجموع الدوال

أمثلة على مشتقات الطرح

بمجرد أن رأينا صيغة مشتقة عملية الطرح، ننتقل الآن إلى تحليل عدة أمثلة لمشتقات هذا النوع من العمليات لفهم كيفية اشتقاق عمليات الطرح بشكل كامل.

مثال 1: مشتقة طرح الدوال المحتملة

$f(x)=x^3-4x$

مشتقة طرح دالتين تعادل الفرق بين مشتقات كل دالة على حدة. لذلك سنقوم أولاً بحساب مشتقة كل دالة على حدة:

$\cfrac{d}{dx} \ x^3=3x^2$

$\cfrac{d}{dx}\ 4x=4$

وبالتالي فإن مشتق الدالة بأكملها هو ما يلي:

$f'(x)=3x^2-4$

مثال 2: مشتقة طرح دوال مختلفة

$f(x)=\text{cos}(x)-\log_7(x^2)$

للتمييز بين دوال الطرح، يجب عليك أولاً التمييز بين الوظيفتين بشكل منفصل ثم طرحهما.

$\cfrac{d}{dx} \ \text{cos}(x)=-\text{sen}(x)$

$\cfrac{d}{dx}\ \log_7 (x^2)=\cfrac{2x}{x^2\cdot \ln(7)}=\cfrac{2}{x\ln(7)}$

وبعد عمل المشتقتين نطرحهما بنفس الترتيب الأولي:

$f'(x)=-\text{sen}(x)-\cfrac{2}{x\ln(7)}$

مثال 3: مشتقة الطرح التربيعي

$f(x)=\left(x^7-2x^3-9\right)^2$

في هذه الحالة لدينا دالة مركبة، لأنها عملية طرح بين ثلاث دوال مربعة. لذلك يجب علينا استخدام صيغة مشتقة دالة محتملة وقاعدة السلسلة لحساب مشتقة الدالة بأكملها:

$f(x)=2\left(x^7-2x^3-9\right)\cdot \left(7x^6-6x^2\right)$