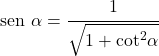ستجد في هذه الصفحة كل شيء عن دالة الجيب: ما هي، ما هي صيغتها، كيفية تمثيلها في الرسم البياني، خصائص هذا النوع من الوظائف، السعة، الدورة، إلخ. بالإضافة إلى ذلك، سوف تكون قادرًا على رؤية أمثلة مختلفة لوظائف الجيب لفهم المفهوم بشكل كامل. حتى أنه يشرح نظرية الجيب والعلاقات التي تربط دالة الجيب بالنسب المثلثية الأخرى.
صيغة دالة الجيب
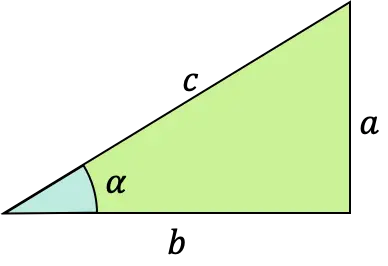
دالة الجيب للزاوية α هي دالة مثلثية يتم تعريف صيغتها على أنها النسبة بين الساق المقابلة والوتر في المثلث القائم (مثلث ذو زاوية قائمة).

غالبًا ما يُكتب هذا النوع من الوظائف الرياضية بالاختصار “sin” أو “sin” (من الكلمة اللاتينية sinus ). بالإضافة إلى ذلك، يمكن أن يطلق عليها أيضًا وظيفة جيبية، أو جيبية، أو جيبية.
دالة الجيب هي واحدة من أشهر النسب المثلثية، إلى جانب جيب التمام وظل الزاوية.
القيم المميزة لوظيفة الجيب
تتكرر بعض الزوايا بشكل متكرر، وبالتالي، من المناسب معرفة قيمة دالة الجيب عند هذه الزوايا:
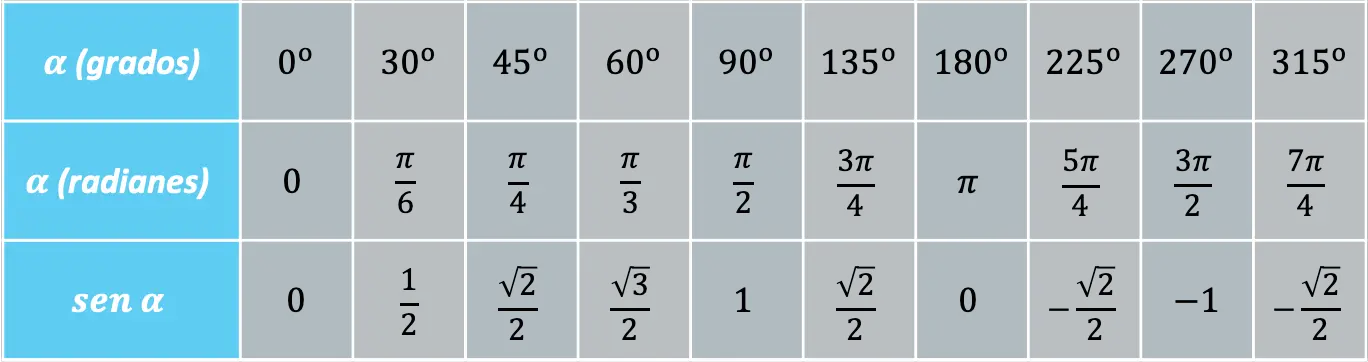
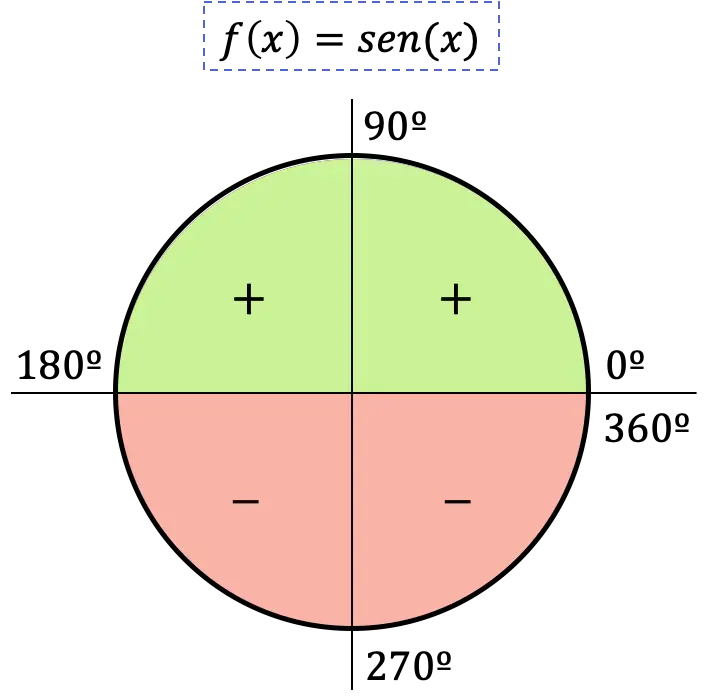
وبالتالي فإن إشارة دالة الجيب تعتمد على الربع الذي تقع فيه الزاوية: فإذا كانت الزاوية في الربع الأول أو الثاني يكون الجيب موجباً، أما إذا كانت الزاوية تقع في الربع الثالث أو الرابع ، سيكون الجيب سالبًا.
تمثيل رسومي لوظيفة الجيب
باستخدام جدول القيم الذي رأيناه في القسم السابق، يمكننا رسم دالة الجيب بيانيًا. لذلك، عندما نمثل دالة الجيب بيانيًا، نحصل على:
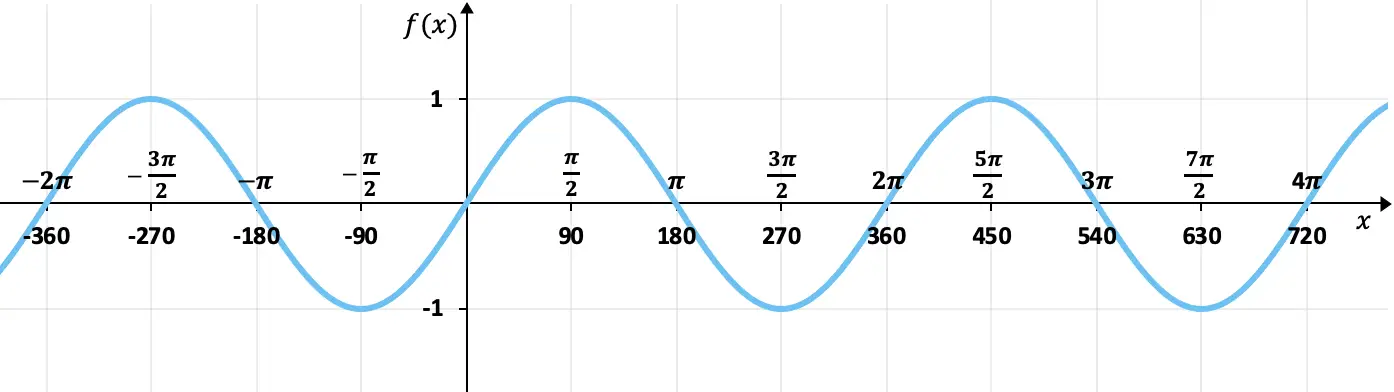
كما ترون من الرسم البياني، فإن قيم صور دالة الجيب تكون دائمًا بين +1 و -1، أي أنها محددة من الأعلى بـ +1 ومن الأسفل بـ -1. بالإضافة إلى ذلك، تتكرر القيم كل 360 درجة (2π راديان)، لذا فهي دالة دورية دورتها 360 درجة.
من ناحية أخرى، في هذا الرسم البياني نقدر تمامًا أن دالة الجيب غريبة، لأن عناصرها المتقابلة لها صور متقابلة، أو بمعنى آخر، فهي متناظرة بالنسبة إلى الأصل (0،0). على سبيل المثال، جيب الزاوية 90 درجة يساوي 1 وجيب الزاوية -90 درجة يساوي -1.
خصائص وظيفة الجيب
تتميز وظيفة الجيب بالخصائص التالية:
- مجال دالة الجيب هو كل الأعداد الحقيقية، لأنه، كما يوضح الرسم البياني، توجد الدالة لأي قيمة للمتغير المستقل x.
![]()
- مسار أو نطاق دالة الجيب هو من سالب 1 إلى زائد 1 (كلاهما شامل).
![]()
- إنها دالة مستمرة وغريبة بدورية 2π.
![]()
- هذا النوع من الدوال المثلثية له نقطة تقاطع واحدة مع المحور y (المحور Y) عند النقطة (0,0).
![]()
- بدلاً من ذلك، فإنه يعترض بشكل دوري الإحداثي السيني (المحور X) عند عدة إحداثيات لـ pi.
![]()
- الحد الأقصى لدالة الجيب يحدث عندما:
![]()
- وعلى العكس من ذلك، فإن الحد الأدنى لدالة الجيب يحدث عند:
![]()
- مشتق دالة الجيب هو جيب التمام:
![]()
- أخيرًا، تكامل دالة الجيب هو علامة تغير جيب التمام:
![]()
الدورة وسعة وظيفة الجيب
وكما رأينا في الرسم البياني الخاص به، فإن دالة الجيب هي دالة دورية، أي أن قيمها تتكرر حسب التردد. بالإضافة إلى ذلك، فإن القيم القصوى والدنيا التي تتأرجح بينها تعتمد على اتساعها. ولذلك فإن الخاصيتين اللتين تحددان الدالة الجيبية هما مدتها وسعةها:
![]()
- دورة دالة الجيب هي المسافة بين نقطتين يتكرر عندهما الرسم البياني ويتم حسابها بالصيغة التالية:
![]()
- سعة دالة الجيب تعادل المعامل الموجود أمام حد الجيب.
![]()
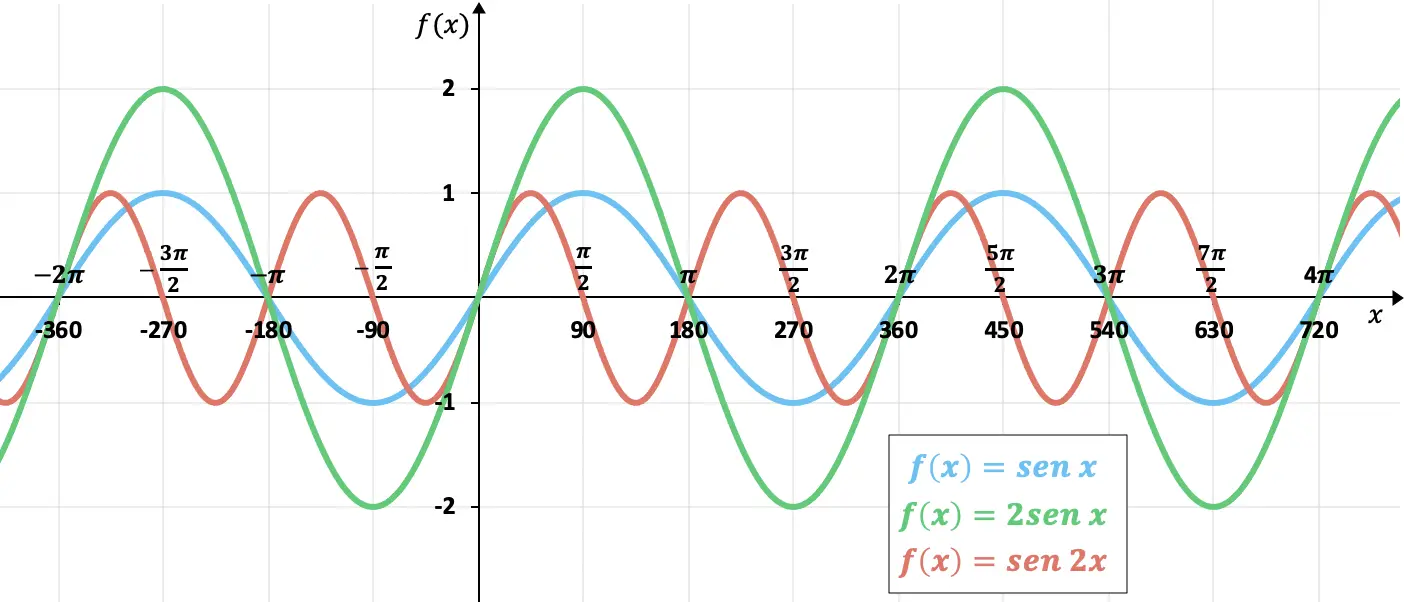
يمكنك أدناه رؤية رسم بياني يوضح تأثيرات تغيير الفترة أو السعة:

في الدالة الموضحة باللون الأخضر، يمكننا أن نرى أنه من خلال مضاعفة السعة، تنتقل الدالة من +2 إلى -2، بدلاً من +1 إلى -1. من ناحية أخرى، في الدالة الموضحة باللون الأحمر، يمكنك أن ترى كيف أنها تسير بسرعة مضاعفة مثل دالة الجيب “المعتمدة”، حيث تم تخفيض دورها إلى النصف.
نظرية الجيب
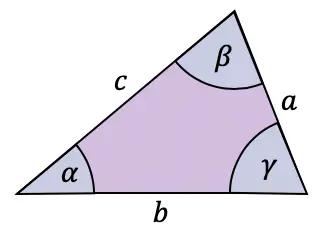
على الرغم من أن جيب الجيب يطبق عادةً على المثلثات القائمة، إلا أن هناك أيضًا نظرية تنطبق على أي نوع من المثلثات: نظرية الجيب (الجيبات).
قانون الجيب يربط بين أضلاع وزوايا أي مثلث كما يلي:
![]()
علاقات دالة الجيب بالنسب المثلثية الأخرى
ستجد أدناه العلاقات الجيبية مع أهم النسب المثلثية في علم المثلثات.
نسبة جيب التمام
- الرسم البياني لوظيفة جيب التمام يعادل منحنى الجيب ولكنه تحول
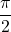
إلى اليسار، بحيث يمكن ربط الوظيفتين بالتعبير التالي:
![]()
- يمكنك أيضًا ربط الجيب وجيب التمام بالهوية المثلثية الأساسية:
![]()
العلاقة مع الظل
- على الرغم من صعوبة إثباته، إلا أنه لا يمكن التعبير عن جيب الجيب إلا وفقًا للظل:
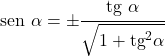
العلاقة مع قاطع التمام
- الجيب وقاطع التمام عبارة عن معكوسين ضربيين:
![]()
العلاقة مع القاطع
- يمكن مسح الجيب بحيث يعتمد فقط على القاطع:
![]()
العلاقة مع ظل التمام
- يرتبط جيب الزاوية وظل التمام بالمعادلة التالية: