ستجد في هذه الصفحة شرحًا لماهية المصفوفة عديمة القدرة، بالإضافة إلى عدة أمثلة حتى تتمكن من فهمها وعدم الشك فيها. بالإضافة إلى ذلك، سوف تكون قادرًا على رؤية هياكل المصفوفات عديمة القدرة وجميع خصائص هذه الأنواع من المصفوفات.
ما هي المصفوفة عديمة القدرة؟
تعريف المصفوفة غير الفعالة هو كما يلي:
المصفوفة المعدومة هي مصفوفة مربعة مرفوعة إلى عدد صحيح تعطي المصفوفة الصفرية .
![]()
ذهب
![]()
هي المصفوفة عديمة القدرة و
![]()
أس القوة التي تعطي المصفوفة الصفرية.
هذا الشرط لا يعني أن أس المصفوفة عديمة القدرة تعطي صفرًا دائمًا بغض النظر عن الأس، بل يعني أنه إذا كان هناك قوة واحدة على الأقل للمصفوفة تكون نتيجتها مصفوفة مليئة بالصفر، فإن المصفوفة عديمة القدرة.
من ناحية أخرى، فإن مؤشر العجز لمصفوفة عديمة القدرة هو أصغر رقم يتم به استيفاء شرط العجز. يمكننا أيضًا أن نقول أن المصفوفة عديمة القدرة هي من الرتبة k ، حيث k هو مؤشر عدم القدرة.
أمثلة على المصفوفات عديمة القدرة
للانتهاء من فهم مفهوم المصفوفة عديمة القدرة، سنرى عدة أمثلة على هذا النوع من المصفوفات:
مثال على مصفوفة عديمة القدرة 2 × 2
المصفوفة المربعة التالية ذات البعد 2×2 غير فعالة:
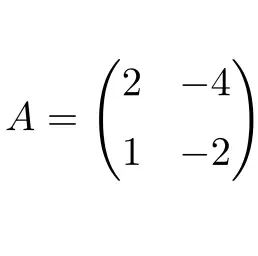
المصفوفة معدومة لأنه من خلال تربيع المصفوفة A نحصل على المصفوفة الصفرية كنتيجة:
![Rendered by QuickLaTeX.com \displaystyle A^2=\begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}\cdot \begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}=\begin{pmatrix} \bm{0} &\bm{0} \\[1.1ex] \bm{0} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fde370dd31b0e2a533fdf1e9d23cf2c9_l3.png)
وبالتالي فهي مصفوفة عديمة القدرة ومؤشر عدم القدرة الخاص بها هو 2، حيث يتم الحصول على المصفوفة الصفرية للقوة الثانية.
مثال على مصفوفة عديمة القدرة 3×3
المصفوفة المربعة التالية من الرتبة 3 غير فعالة:
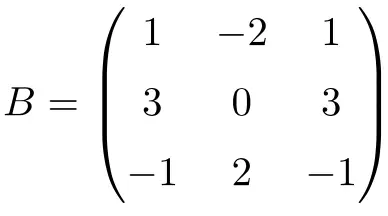
على الرغم من أننا برفع المصفوفة إلى 2 لا نحصل على المصفوفة الصفرية:
![Rendered by QuickLaTeX.com \displaystyle B^2=\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}\cdot \begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fbad4ccc270e2960ae50cc23eacc7530_l3.png)
لكن عند حساب مكعب المصفوفة، نحصل على مصفوفة جميع عناصرها تساوي 0:
![Rendered by QuickLaTeX.com \displaystyle B^3= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}\cdot\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}\bm{0}&\bm{0}&\bm{0}\\[1.1ex]\bm{0}&\bm{0}&\bm{0}\\[1.1ex] \bm{0}&\bm{0}&\bm{0}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-da876a04b14d80c156e24c95bd22372e_l3.png)
لذا فإن المصفوفة B هي مصفوفة عديمة القدرة، وبما أن المصفوفة الصفرية يتم الحصول عليها للأس 3، فإن مؤشر عدم القدرة الخاص بها هو 3.
هيكل مصفوفة عديمة القدرة 2 × 2
أدناه يمكنك رؤية هيكل جميع المصفوفات غير القادرة. إن إثباتها ممل بعض الشيء، لذلك تركنا لك مباشرة الصيغة للحصول على مصفوفة عديمة القدرة من الرتبة 2:
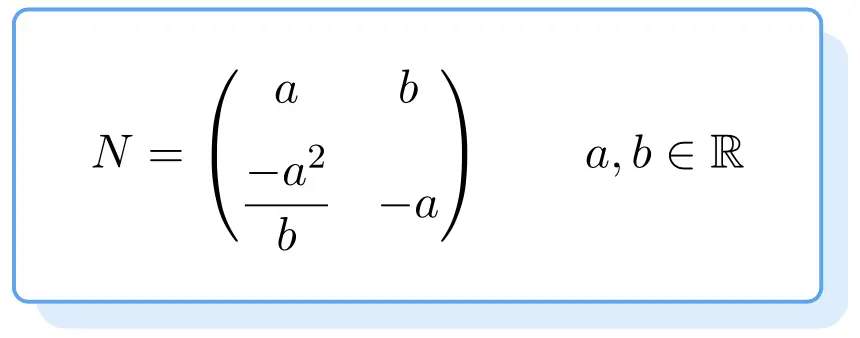
لذا فإن أي مصفوفة تفي بالصيغة المذكورة أعلاه ستكون مصفوفة عديمة القدرة. ولهذا القيم
![]()
و
![]()
يمكن أن تكون عشوائية طالما أنها أرقام حقيقية.
خصائص المصفوفات عديمة القدرة
تتميز المصفوفات غير الفعالة بالخصائص التالية:
- أثر المصفوفة عديمة القدرة هو دائمًا صفر.
- وبالمثل، فإن محدد أي مصفوفة عديمة القدرة هو دائمًا 0. لكن العكس ليس صحيحًا، أي أن محدد المصفوفة صفر لا يعني أن المصفوفة عديمة القدرة.
- المصفوفة الوحيدة عديمة القدرة التي يمكن قطريًا هي المصفوفة الصفرية.
- إن مؤشر العجز لمصفوفة عديمة القدرة ذات البعد n×n يساوي دائمًا أو أقل من n . وهذا هو السبب في أن مؤشر العجز لمصفوفة عدم القدرة 2 × 2 سيكون دائمًا 2.
- المصفوفة المعدومة ليست قابلة للعكس.
- أيمصفوفة مثلثة ذات أصفار على القطر الرئيسي هي أيضًا مصفوفة عديمة القدرة.
- هناك نظرية تقول أنه إذا كانت المصفوفة

هو عديم القدرة، ثم المصفوفة
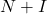
غير قابل للعكس، حيث
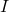
هي مصفوفة الهوية. بالإضافة إلى ذلك، يمكن إيجاد المصفوفة العكسية بالصيغة التالية:
![]()
- بالمثل، إذا

إذا كانت مصفوفة معدومة القدرة، فيمكن حساب معكوس المصفوفة
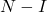
بالمعادلة التالية :
![]()
- أي مصفوفة مفردة، أي غير قابلة للعكس، يمكن أن تتحلل إلى منتج مصفوفات عديمة القدرة.
- جميع القيم الذاتية (أو القيم الذاتية) للمصفوفة عديمة القدرة هي صفر.
![]()
- وأخيرًا، من باب الفضول، هناك أيضًا مفهوم التحول غير الفعال، والذي يحدد التطبيق الخطي
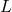
من الفضاء المتجه من هذا القبيل
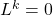
.