ذوات الحدين

ستجد في هذه الصفحة شرحًا لماهية ذات الحدين، وبالإضافة إلى ذلك، ستتمكن من رؤية أمثلة لكل نوع من أنواع ذات الحدين. نعرض لك أيضًا الصيغ المستخدمة لحل العمليات ذات الحدين: ضرب ذات الحدين، تربيع ذات الحدين، تكعيب ذات الحدين،…

ما هو الزوج؟

في الجبر، تعريف ذات الحدين هو:

ذات الحدين هي كثيرة الحدود تتكون من وحدتين فقط . بمعنى آخر، تتكون ذات الحدين من تعبير جبري به حدين مختلفين فقط مرتبطين بعلامة الجمع (+) أو علامة الطرح (-).

كلمة ذات الحدين تأتي من اللغة اليونانية وتتكون من مكونين معجميين ( bi و nomos )، والتي تعني ما يلي:

ثنائية : بادئة بمعنى 2.
نوموس : يعني جزء.

يمكننا بالتالي استنتاج معنى ذات الحدين: كثيرة الحدود ذات جزأين (أو وحدتين).

ومن ناحية أخرى، فإن مفهوم الزوج له معنى آخر غير المعنى الرياضي، وهو أنه يمكن للزوج أيضًا تعيين مجموعة من شخصيتين لهما دور قيادي في الحياة السياسية، أو في بعض التخصصات الرياضية أو حتى في الترفيه. . لكن من الواضح أننا سنركز هنا على التعريف الرياضي ذي الحدين.

أمثلة على ذات الحدين

للانتهاء من فهم مفهوم ذات الحدين، سنرى عدة أمثلة على هذا النوع من كثيرات الحدود:

مثال على ذات الحدين من الدرجة الثانية:

$x^2+4x$

مثال على ذات الحدين من الدرجة الثالثة:

$x^3+5$

مثال على ذات الحدين من الدرجة الرابعة:

$3x^4+8x^2$

الآن بعد أن عرفنا ما هي ذات الحدين، سنرى الأنواع المختلفة من ذات الحدين الموجودة وكيفية حل العمليات مع ذات الحدين.

ذات الحدين التربيعية

ذات الحدين المربعين هي هوية رائعة، وتسمى أيضًا المنتج الرائع أو المساواة الرائعة. يعتمد حل قوة ذات الحدين المرفوعة إلى 2 على ما إذا كانت عبارة عن مجموع ذي الحدين أو فرق ذي الحدين.

يشير مجموع ذو الحدين إلى ذلك الحدين الذي يكون حداه موجبين، أي أن مجموع الحدين المربع هو:

$(a+b)^2$

من ناحية أخرى، فإن الفرق (أو الطرح) ذو الحدين هو مرافق الجمع ذو الحدين، وهذا يعني أن أحد أحاديات الحد له علامة سلبية. ولذلك، فإن التعبير الجبري للفرق التربيعي ذي الحدين هو:

$(a-b)^2$

لحساب ذات الحدين المربعين، يجب عليك تطبيق صيغة، كما رأينا، تختلف اعتمادًا على ما إذا كانت إضافة أو طرحًا. اكتشف كيفية القيام بذلك في صيغ المساواة البارزة ، حيث يمكنك رؤية جميع الشروحات خطوة بخطوة بالإضافة إلى الأمثلة والتمارين التي تم حلها، وليس فقط هاتين المتساويتين البارزتين، بل جميعهما.

مكعب ذو الحدين

على الرغم من أنها أقل استخدامًا، إلا أن ذات الحدين المكعب تعتبر أيضًا منتجات بارزة. أو بمعنى آخر، هناك قواعد رياضية تسمح لك بالعثور بسرعة على مكعب ذات الحدين (يمكنك رؤيتها في الرابط أعلاه الخاص بصيغ المتطابقات البارزة ).

كما كان من قبل، تعتمد نتيجة هذا التقوية على ما إذا كان مكعبًا للمجموع:

$(a+b)^3$

أو على العكس من ذلك، إذا كانت القوة مكونة من مكعب الفرق أو الطرح:

$(a-b)^3$

منطقيا، الفرق الرئيسي بين ذات الحدين التربيعي وذو الحدين المكعب هو الأس. ومع ذلك، فإن صيغة ذات الحدين المكعب أكثر تعقيدًا بكثير من صيغة ذات الحدين المربعة.

اتفاقيات بارزة

هناك على وجه الخصوص أنواع معينة من ذوات الحدين والتي تكون خاصة بعض الشيء بسبب خصائصها، لأنها تتوافق مع هويات بارزة أقل شهرة (أو منتجات بارزة).

مجموع المربعات:
$a^2+b^2$
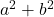
فرق (أو طرح) المربعات:
$a^2-b^2$
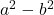
مجموع المكعبات:
$a^3+b^3$
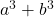
فرق (أو طرح) المكعبات:
$a^3-b^3$

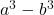
ذهب

$a$

$b$

هل هناك أي اثنين من أحاديات الحد.

على الرغم من أن هذه التعبيرات ذات الحدين تشبه إلى حد كبير تلك التي رأيناها أعلاه (مربع ذات الحدين ومكعب ذي الحدين)، إلا أنها مختلفة إذا نظرت عن كثب. وبهذا المعنى، يمكنك أيضًا الاطلاع على صيغ ذات الحدين البارزين واستنتاجاتها من خلال النقر على الرابط أعلاه ⬆ صيغ المتطابقات البارزة.⬆

الضرب ذو الحدين

واحدة من العمليات الأكثر شيوعا مع ذات الحدين هي الضرب. لذا سنرى بعد ذلك مثالاً لكيفية حساب الضرب بين ذوات الحدين.

$(x^2+2x)\cdot (x-5)$

لحساب ضرب ذي الحدين، يجب علينا أولاً ضرب كل حد في ذات الحدين الأول بكل حد في الحدين الثاني:

$x^2\cdot x+x^2\cdot (-5)+2x\cdot x +2x\cdot (-5)$

$x^3-5x^2+2x^2 -10x$

بعد ذلك، نقوم بتجميع المصطلحات المتشابهة، أي أنها تحتوي على نفس الجزء الحرفي:

$\bm{x^3-3x^2 -10x}$

وبهذه الطريقة تمكنا من إيجاد نتيجة المنتج بين الأزواج.

نتاج اثنين من الحدين مع مصطلح مشترك

عندما يكون للثنائيات التي تشارك في الضرب مصطلح مشترك هو المتغير

$x,$

هناك صيغة لحساب هذه العملية ذات الحدين بسرعة:

$(x+a)(x+b) = x^2+(a+b)x+ab$

نعرض لك هنا تمرينًا تم حله حتى تتمكن من معرفة كيفية تطبيق هذه الصيغة:

$\begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}$

نيوتن ذات الحدين

ذات الحدين لنيوتن ، وتسمى أيضًا نظرية ذات الحدين، هي صيغة تستخدم لحساب قوى ذات الحدين.

الصيغة الرياضية ذات الحدين لنيوتن هي كما يلي:

$\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}x^{n-k}y^k$

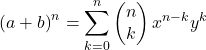
أو ما يعادلها:

$\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}$

كما ترون، هذه الصيغة معقدة بعض الشيء لفهمها. ولهذا السبب قمنا بوضع قوى ذات الحدين من أدنى درجة أدناه حتى تتمكن من فهمها بشكل أفضل:

يمكن أن تكون هذه الصيغة مملة بعض الشيء لحساب ثنائيات الحدين المربعة أو المكعبة، لأنه كما رأينا أعلاه، هناك صيغ أبسط. ومع ذلك، فإن ذات الحدين لنيوتن مفيدة جدًا للعثور على قوى ذات درجة أعلى، على سبيل المثال، يتم استخدامها على نطاق واسع لتحديد ذات الحدين إلى الرابع.

لكن لتطبيق هذه الصيغة، يجب أن تعرف كيفية حساب عدد اندماجي، أي التعبير الجبري من النوع

$\begin{pmatrix} 4 \\ 2 \end{pmatrix}$

، الحساب ليس سهلا. 🔍 ولهذا ننصحك بالبحث عن كيفية إجراء ذلك في محرك البحث الخاص بنا في أعلى اليمين 🔎، ستجد مقالنا حيث نشرح لك هذه العملية خطوة بخطوة.