مصفوفة متماثلة

ستجد في هذه الصفحة شرحًا لماهية المصفوفات المتماثلة. بالإضافة إلى ذلك، نعرض لك كيفية التعرف بسرعة على ما إذا كانت المصفوفة متماثلة، إلى جانب العديد من الأمثلة حتى لا تكون لديك أي شكوك. ستجد أيضًا جميع خصائص المصفوفات المتماثلة. وأخيرًا، نوضح ميزة معينة تتمتع بها أي مصفوفة مربعة: حيث يمكن تحليلها إلى مجموع مصفوفة متماثلة ومصفوفة غير متماثلة.

ما هي المصفوفة المتماثلة؟

تعريف المصفوفة المتماثلة هو كما يلي:

المصفوفة المتماثلة هي مصفوفة مربعة يكون نقلها مساويًا للمصفوفة نفسها.

$A^t = A$

ذهب

$A^t$

يمثل المصفوفة المنقولة

$A$

بمجرد أن تعرفنا على مفهوم المصفوفة المتماثلة، سنرى كيف يمكن التعرف على أي مصفوفة متماثلة بسهولة:

متى تكون المصفوفة متماثلة؟

يعد التعرف على بنية المصفوفة المتماثلة أمرًا بسيطًا للغاية: يجب أن يكون عنصر الصف i والعمود j مطابقًا لعنصر الصف j والعمود i . ويمكن أن تكون قيم القطر الرئيسي للمصفوفة موجودة.

أمثلة على المصفوفات المتماثلة

فيما يلي عدة أمثلة للمصفوفات المتماثلة لمساعدتك على الفهم:

مثال لمصفوفة متماثلة من الرتبة 2 × 2

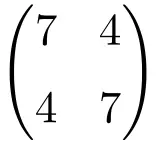
مثال لمصفوفة متماثلة البعد 3×3

مثال لمصفوفة متماثلة بحجم 4×4

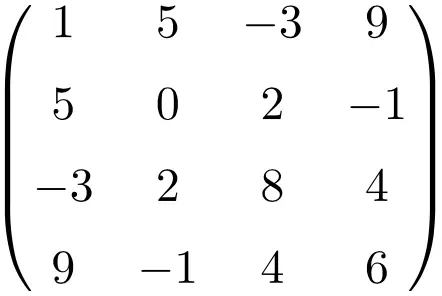
وبنقل هذه المصفوفات الثلاث نتحقق من تماثلها، لأن المصفوفات المنقولة تعادل مصفوفاتها الأصلية.

لماذا سميت بالمصفوفة المتماثلة؟

إذا نظرت عن كثب إلى الأمثلة السابقة، فإن القطر الرئيسي للمصفوفة المتماثلة هو محور التماثل، أو بمعنى آخر، يعمل كمرآة بين الأرقام الموجودة فوق القطر وتلك الموجودة أسفله. ولهذا السبب، تسمى هذه الأنواع من المصفوفات متماثلة.

خصائص المصفوفات المتماثلة

خصائص المصفوفات المتماثلة هي كما يلي:

إن إضافة (أو طرح) مصفوفتين متماثلتين يعطي مصفوفة متماثلة أخرى. نظرًا لأن نقل مصفوفتين مضافتين (أو مطروحتين) يعادل نقل كل مصفوفة على حدة:

$\displaystyle \left(A+B\right)^t = A^t+B^t = A+B$

أي مصفوفة متماثلة مضروبة في عددية تؤدي أيضًا إلى ظهور مصفوفة متماثلة أخرى.

وبالمثل، فإن حاصل ضرب المصفوفة بين مصفوفتين متماثلتين لا يساوي دائمًا مصفوفة متماثلة أخرى، فقط إذا كان من الممكن تبديل المصفوفتين. يمكن إثبات هذا الشرط باستخدام خاصية ضرب المصفوفة المنقولة:

$\displaystyle \left(A\cdot B\right)^t = B^t\cdot A^t = BA=AB$

قوة المصفوفة المتماثلة تؤدي إلى ظهور مصفوفة متماثلة أخرى، طالما أن الأس عدد صحيح.

من الواضح أن المصفوفة الوحدوية والمصفوفة الصفرية هما مثالان على المصفوفات المتماثلة.

المصفوفة المتطابقة مع المصفوفة المتماثلة يجب أن تكون متماثلة أيضًا.

إذا كانت المصفوفة المتماثلة منتظمة أو قابلة للعكس، فإن مصفوفتها العكسية تكون متماثلة أيضًا.

الأمر نفسه ينطبق على المصفوفة المجاورة للمصفوفة المتماثلة: المصفوفة المجاورة لمصفوفة متماثلة تعطي مصفوفة متماثلة أخرى كحل.

المصفوفة المتماثلة الحقيقية هي أيضًا مصفوفة عادية.

بما أن المصفوفات المتماثلة هي حالة خاصة من المصفوفات الهرمسية، فإن جميع القيم الذاتية (أو القيم الذاتية) للمصفوفة المتماثلة هي أرقام حقيقية.

تخبرنا النظرية الطيفية أن جميع المصفوفات التي عناصرها حقيقية هي مصفوفات قابلة للقطر، علاوة على ذلك، يتم إجراء القطر عن طريق مصفوفة متعامدة. ولذلك، فإن جميع المصفوفات المتماثلة الحقيقية تكون متعامدة قطريًا.

من ناحية أخرى، يمكن قطريًا المصفوفات المتماثلة ذات الأعداد المركبة من خلال مصفوفة وحدوية.

مصفوفة هسه دائما متماثلة.

تحلل المصفوفة المربعة إلى مصفوفة متماثلة ومصفوفة غير متماثلة

الميزة الخاصة للمصفوفات المربعة هي أنها يمكن أن تتحلل إلى مجموع مصفوفة متماثلة بالإضافة إلى مصفوفة غير متماثلة.

الصيغة التي تسمح لنا بالقيام بذلك هي كما يلي:

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

حيث C هي المصفوفة المربعة التي نريد تحليلها، C ^t تبديلها، وأخيرًا S و A هما على التوالي المصفوفات المتماثلة وغير المتماثلة التي تتحلل فيها المصفوفة C.

يوجد أدناه تمرين تم حله لمعرفة كيفية القيام بذلك. دعونا نحلل المصفوفة التالية:

$\displaystyle C=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

نحسب المصفوفة المتماثلة وغير المتماثلة بالصيغ:

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}$

ويمكننا التأكد من تحقق المعادلة عن طريق جمع المصفوفتين:

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}+\begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

$\displaystyle C=S+A$

✅