وحيدات الحد

نوضح هنا كل ما تحتاج لمعرفته حول وحيدات الحد: ما هي، وما هي أجزائها (وكيفية التعرف عليها)، والأنواع المختلفة من وحيدات الحد، وكيفية حساب العمليات مع وحيدات الحد، والقيمة العددية لوحيدات الحد،. .. بالإضافة إلى ذلك، ستتمكن من رؤية أمثلة وتمارين تم حلها خطوة بخطوة لوحيدات الحد.

ما هي أحاديات الحد؟

في الرياضيات، تعريف أحادي الحد هو كما يلي:

أحادي الحد هو تعبير جبري يتكون من مزيج من الأرقام والحروف. بتعبير أدق، تتكون أحادية الحد من حاصل الضرب بين رقم ومتغير واحد أو أكثر (حروف) مرفوعًا إلى الأسس.

على سبيل المثال، يسمى الحد 7x ³ y ² وحيد الحد لأنه يحتوي على رقم (7) وأحرف مختلفة (x، y).

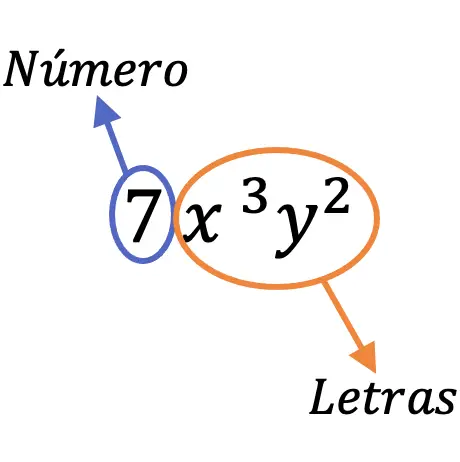
أجزاء من أحادية الحد

الآن بعد أن رأينا معنى أحادية الحد، دعونا نرى ما هي جميع أجزاء أحادية الحد:

المعامل : هو الرقم الذي يضرب متغيرات (أو أحرف) أحادية الحد.
المتغير : هو كل حرف من الحروف التي تظهر في أحادية الحد .
الجزء الحرفي : يتوافق مع جميع المتغيرات التي تشكل أحادية الحد مع جميع الأسس الخاصة بها.
الدرجة : تتكون من مجموع جميع أسس الحروف التي تشكل أحادية الحد.

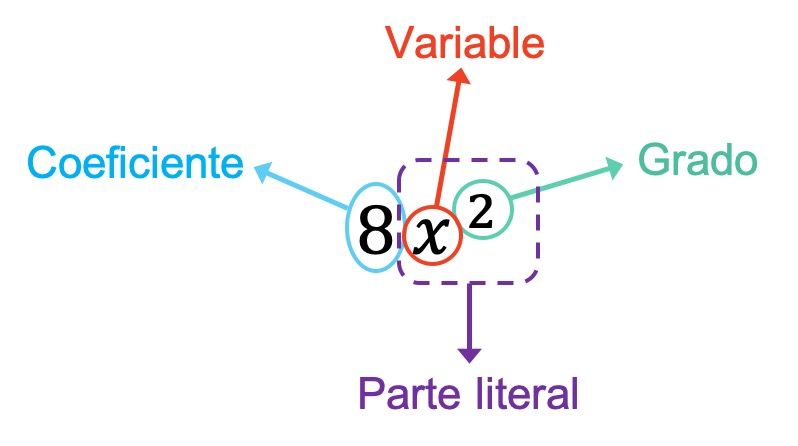
معامل وحيدة الحد في المثال أعلاه هو 8 لأنه الرقم الذي يضرب المتغيرات. أيضًا، في هذه الحالة، تحتوي أحادية الحد على متغير واحد فقط، وهو x. إذن، الجزء الحرفي من أحادية الحد يتكون من هذا المتغير بالإضافة إلى أسه، وهو x ² . وأخيرًا، درجة أحادية الحد هي 2 لأنها الأس الوحيد لها.

والآن حاول حل التمرين التالي على أجزاء أحادية الحد:

حدد جميع أجزاء أحادية الحد التالية:

$5x^4y^2z$

انظر الحل

مكونات monomial من البيان هي:

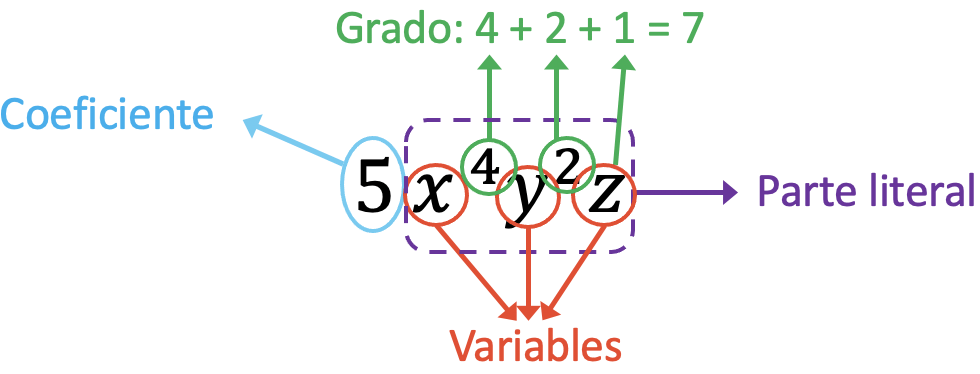
معامل وحيدة الحد في المسألة هو 5، لأنه الحد الذي يضاعف الحروف. من ناحية أخرى، فإن متغيرات هذا الحد هي x، y، z. ثالثًا، الجزء الحرفي من أحادية الحد يتوافق مع التعبير x ⁴ y ² z. وأخيرًا، درجة أحادية الحد تساوي مجموع جميع أسس المتغيرات، أي 7 (4+2+1=7).

لاحظ أنه عندما لا يكون للحرف أس، فهذا يعني في الواقع أنه يحتوي على 1 كأس له. لذلك، لحساب درجة أحادية المشكلة، نضيف وحدة تمثل أس المتغير z.

أنواع أحاديات الحد

هناك أنواع مختلفة من أحاديات الحد، ولكل منها خصائصها الخاصة. أهم أحاديات الحد هي أحاديات الحد المتشابهة، ووحيدات الحد المتجانسة، ووحيدات الحد غير المتجانسة، ووحيدات الحد المعاكسة. وبعد ذلك سنرى خصائص كل نوع.

أحادية الحد مماثلة

وحيدات الحد المشابهة هي أحاديات الحد التي لها نفس الجزء الحرفي. ولذلك، فإن اثنين أو أكثر من وحيدات الحد تكون متشابهة عندما يكون لها نفس الحروف والأسس.

على سبيل المثال، تتشابه وحدتا الحد التاليتان، لأنه على الرغم من أن لهما معاملات مختلفة، إلا أنهما يتكونان من نفس المتغيرات ويرفعان إلى نفس الأسس.

$4x^5y^3 \qquad \qquad 9x^5y^3$

وكما سنرى لاحقًا، يُستخدم هذا النوع من وحيدات الحد لحل العمليات على وحيدات الحد.

أحاديات متجانسة

يكون اثنان من أحاديات الحد متجانسين عندما تكون درجتهما المطلقة متساوية.

على سبيل المثال، وحيدات الحد التالية متجانسة لأن درجة كل منهما تساوي 5:

$2x^5 \qquad \qquad 6x^2y^3$

أحادية الحد الأولى لها متغير واحد مرفوع للأس 5، إذن درجتها هي 5. وكثيرة الحدود الثانية لها متغير واحد مربع وآخر مكعب، لذا درجتها أيضًا 5 (2+ 3 =5).

كما ترون، لكي يكون اثنان من أحاديات الحد متجانسين، لا يحتاجان إلى أن يكون لهما نفس الجزء الحرفي، ولكن فقط أن يكون لهما نفس الدرجة المطلقة.

أحاديات الحد غير المتجانسة

وحيدات الحد غير المتجانسة هي أحاديات الحد التي ليس لها نفس الدرجة المطلقة. وبعبارة أخرى، وحيدات الحد غير المتجانسة هي عكس أحاديات الحد المتجانسة.

تعتبر أحاديات الحد الثلاثة التالية غير متجانسة لأن لكل منها درجة مختلفة:

$x^8 \qquad 3xy \qquad 7a^9b^2$

أحادية الحد الأولى هي من الدرجة 8، ووحيدة الحد الثانية هي من الدرجة 2، ووحيدة الحد الثالثة هي من الدرجة 11. وبالتالي، فإن أحاديات الحد الثلاثة غير متجانسة مع بعضها البعض.

ضد أحاديات الحد

مقابل وحيدات الحد هي وحيدات الحد المتجانسة (لها نفس الجزء الحرفي)، علاوة على ذلك، معاملاتها متضادة، أي أن معاملاتها لها نفس القيمة ولكن بإشارة معاكسة.

على سبيل المثال، وحيدات الحد التالية متضادة:

$3x^5y^2 \qquad \qquad -3x^5y^2$

وحيدتا الحد السابقتان متضادان لأنهما يختلفان فقط في إشارتهما، فالأول له إشارة موجبة والثاني له إشارة سالبة.

الآن بعد أن رأيت العديد من الأمثلة على أحاديات الحد، قد تكون مهتمًا بتعبير جبري مماثل آخر: ذو الحدين . في الواقع، تتكون ذات الحدين من جمع (أو طرح) عدة أحاديات الحد، لذلك من المثير للاهتمام رؤية العلاقة بين هذين المفهومين. يمكنك معرفة معنى ذات الحدين بالضغط على هذا الرابط.

العمليات مع وحيدات الحد

لتعميق مفهوم وحيدات الحد، سنرى ما هي العمليات التي يمكن إجراؤها باستخدام وحيدات الحد. على وجه الخصوص، يمكن جمع وطرح وضرب وتقسيم وحيدات الحد والقوة. ولكل نوع من العمليات خصائصه الخاصة، لذلك سنقوم بتحليلها واحدة تلو الأخرى بشكل منفصل أدناه.

مجموع أحاديات الحد

لا يمكن إضافة اثنين أو أكثر من وحيدات الحد إلا إذا كانت أحادية الحد متشابهة. ومن ثم فإن مجموع وحدتين متماثلتين يساوي وحدة حد أخرى مكونة من نفس الجزء الحرفي ومجموع معاملات هاتين الوحيدتين.

أمثلة على مجموع أحاديات الحد

$2x^4+3x^4 = 5x^4$
$4y^2+y^2 = 5y^2$
$7x^3y+2x^3y = 9x^3y$
$2a^3b^2c^6+6a^3b^2c^6 = 8a^3b^2c^6$
$4x^3+2x^3+5x^3=6x^3+5x^3=11x^3$

إذا كنت ترغب في التدرب على تمارين جمع أحاديات الحد، يمكنك البحث عنها في محرك البحث في أعلى اليمين، لأن لدينا صفحة كاملة مليئة بتمارين جمع أحاديات الحد التي تم حلها.

طرح أحاديات الحد

لا يمكن طرح اثنين أو أكثر من أحاديات الحد إلا إذا كانت أحادية الحد متشابهة. وبالتالي فإن طرح وحدتين متشابهتين يساوي أحادية حد أخرى مكونة من نفس الجزء الحرفي وطرح معاملات هاتين الحدتين.

أمثلة على طرح أحاديات الحد

$7x^2-4x^2 = 3x^2$
$5y^3-y^3 = 4y^3$
$8x^6y-4x^6y = 4x^6y$
$10a^3b^4c^2-6a^3b^4c^2 = 4a^3b^4c^2$
$11x^3-4x^3-5x^3=7x^3-5x^3=2x^3$

يمكنك التدرب على تمارين الطرح أحادية الحد التي تم حلها خطوة بخطوة والتي يمكن العثور عليها على موقعنا. يمكنك العثور عليها عبر محرك البحث في أعلى اليمين.

مضاعفة أحاديات الحد

نتيجة ضرب وحدتين هي وحيدة حد أخرى معاملها هو حاصل ضرب معاملات وحيدات الحد ويتم الحصول على جزئها الحرفي بضرب المتغيرات التي لها نفس الأساس، أي بإضافة عارضاتها.

لذا، لحل المنتج بين وحدتين مختلفتين، يجب ضرب المعاملات معًا وإضافة أسس القوى التي لها نفس الأساس.

من ناحية أخرى، إذا قمنا بضرب وحدتين لهما قوة أساسية مختلفة، فعلينا ببساطة أن نضرب معاملاتهما معًا ونترك القوى كما هي:

$5x^2\cdot 3y^4 = (5\cdot 3) x^2y^4 = 15x^2y^4$

أمثلة على ضرب أحاديات الحد

$6x^4 \cdot 7x^5= (6\cdot 7)x^{4+5} = 42x^9$
$4y \cdot 2y^3 = (4\cdot 2)y^{1+3} = 8 y^4$
$5x^2y^4\cdot (-8x^8y^2)=(5\cdot (-8))x^{2+8}y^{4+2} = -40x^{10}y^6$
$-3x^6y^4 \cdot (-4x^2z)= (-3\cdot (-4)) x^{6+2}y^4z= 12x^8y^4z$
$-3x^8\cdot 4x^5\cdot (-x^2) =-12x^{13}\cdot (-x^2)= 12x^{15}$

للتدرب على حل تمارين ضرب أحاديات الحد خطوة بخطوة، يمكنك الرجوع إلى المقالة المتوفرة لدينا على هذا الموقع. ستجده بسهولة مع محرك البحث في أعلى اليمين.

تقسيم أحاديات الحد

ونتيجة تقسيم وحيدات الحد تكون وحيدة حد أخرى معاملها معادل لحاصل معاملات وحيدات الحد ويتم الحصول على جزئها الحرفي بقسمة المتغيرات التي لها نفس الأساس، أي بطرح عارضاتها.

إذن لتقسيم وحدتين مختلفتين، فإننا ببساطة نقسم المعاملات بينهما ونطرح أسس القوى التي لها نفس الأساس.

أمثلة على تقسيم أحاديات الحد

$7x^6 : 7x^4= (7:7)x^{6-4} = 1x^2=x^2$
$12y^5 : 4y^2= (12:4)y^{5-2} = 3y^3$
$15x^7y^6 :3x^4y^5= (15:3)x^{7-4}y^{6-5} = 5x^3y$
$27x^9y^7 :(-3x^5y^2)= (27:(-3))x^{9-5}y^{7-2}= -9x^4y^5$
$-18x^{13} : 3x^4 : (-2x^7) = -6x^9: (-2x^7) = 3x^2$

إن قسمة وحيدات الحد أصعب مما يبدو، لذا ننصحك بمحاولة حل التمارين التي لدينا حول قسمة وحيدات الحد خطوة بخطوة . أسرع طريقة للعثور عليهم هي من خلال محرك البحث الخاص بنا في أعلى اليمين.

قوة أحادية الحد

لحساب قوة أحادية الحد، يجب رفع كل عنصر من عناصر أحادية الحد إلى الأس الأسي . بمعنى آخر، قوة أحادية الحد تتكون من رفع معاملها ومتغيراتها (الحروف) إلى أس القوة.

تذكر من خواص القوى أننا عندما نرفع حدًا مرفوعًا بالفعل، يتم ضرب الأسين معًا. لهذا السبب ، في قوة أحادية الحد، يتم دائمًا ضرب أس كل حرف في الأس الذي يشير إلى القوة .

أمثلة على صلاحيات monomials

$\left(5x^6\right)^2 = 5^2\left(x^6\right)^2 = 5^2x^{6\cdot 2} = 25x^{12}$
$\left(2x^5\right)^4 = 2^4\left(x^5\right)^4 = 2^4x^{5\cdot 4} = 16x^{20}$
$\left(-4y^3\right)^2 = (-4)^2\left(y^3\right)^2 = (-4)^2y^{3\cdot 2} = 16y^{6}$
$\left(3x^4y\right)^3 = 3^3\left(x^4y\right)^3 = 3^3x^{4\cdot 3}y^{1\cdot 3} = 27x^{12}y^3$
$\left(-2a^5b^7\right)^3 = (-2)^3\left(a^5b^7\right)^3 = (-2)^3a^{5\cdot 3}b^{7\cdot 3} = -8a^{15}b^{21}$

من السهل جدًا ارتكاب خطأ في هذا النوع من العمليات باستخدام أحاديات الحد. ولهذا السبب ننصحك بالتدرب على التمارين التي قمنا بحلها خطوة بخطوة على موقعنا. ستجدهم سريعًا من خلال البحث عنهم في محرك البحث أعلى اليمين.

القيمة العددية لمونوميال

القيمة العددية لمونومال هي النتيجة التي يتم الحصول عليها عن طريق استبدال متغيرات مونومال لقيم معينة.

على سبيل المثال، إذا كان لدينا أحادية الحد التالية:

$5x^2$

إذا أردنا إيجاد القيمة العددية للوحدة السابقة لـ

$x=2$

تحتاج إلى استبدال الرسالة

$x$

من أحادية الحد بمقدار 2 وحل العمليات الناتجة:

$5\cdot 2^2= 5 \cdot 4 = 20$

إذن القيمة العددية للوحيدة

$5x^2$

$x=2$

يساوي 20.

يمكنك أيضًا تحديد القيمة العددية لمتغير أحادي الحد. على سبيل المثال، إذا كان لدينا المتغير الثنائي التالي، أو بمعنى آخر المتغير الثنائي، أحادي الحد:

$3x^4y$

لحساب القيمة العددية للوحيد أعلاه متى

$x$

يستحق 1 ه

$y$

هو -2، نستبدل الحروف بقيمها:

$3\cdot 1^4\cdot (-2)= 3 \cdot 1 \cdot (-2) = -6$

لذا فإن القيمة العددية لمونوميال المشكلة

$x=1$

$y=-2$

عوائد-6.

أحاديات ومتعددات الحدود

أخيرًا، اعلم أنه يمكن تكوين كثيرات الحدود من أحاديات الحد:

متعدد الحدود هو تجميع اثنين أو أكثر من أحاديات الحد.

$P(x)= 4x^5+3x^2-7x$

على سبيل المثال، كثير الحدود السابق ينتج عن جمع (أو طرح) 3 أحاديات حد غير متجانسة.

من باب الفضول، عندما تحتوي كثيرة الحدود على وحدتين فقط، فإنها تسمى ذات الحدين . وعندما يكون كثير الحدود لديه 3 أحاديات بالضبط، فإنه يسمى ثلاثي الحدود .

إذا كنت تريد معرفة المزيد عن كثيرات الحدود، يمكنك زيارة الصفحة الرئيسية للويب، حيث نشرح كل ما تحتاج لمعرفته حول كثيرات الحدود.