▷ مشتق المماس (الصيغة والتدريبات المحلولة)

هنا سوف تكتشف كيفية اشتقاق دالة الظل. بالإضافة إلى ذلك، ستتمكن من رؤية أمثلة على مشتقات المماس وحتى التدرب على حل التمارين خطوة بخطوة. وأخيرًا، نعرض أيضًا صيغة مشتقة الظل ونوضح لك صيغة مشتقة الظل العكسي.

ما هو مشتق الظل؟

مشتق ظل x يساوي 1 على مربع جيب تمام x. مشتق ظل x يكافئ أيضًا مربع قاطع x، و1 زائد مربع ظل x.

$\begin{array}{c}f(x)=\text{tan}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cos}^2(x)}=\text{sec}^2(x)=1+\text{tan}^2(x)\end{array}$

جميع التعبيرات متكافئة، لذا فإن دالة الظل لها ثلاث صيغ محتملة لاشتقاقها.

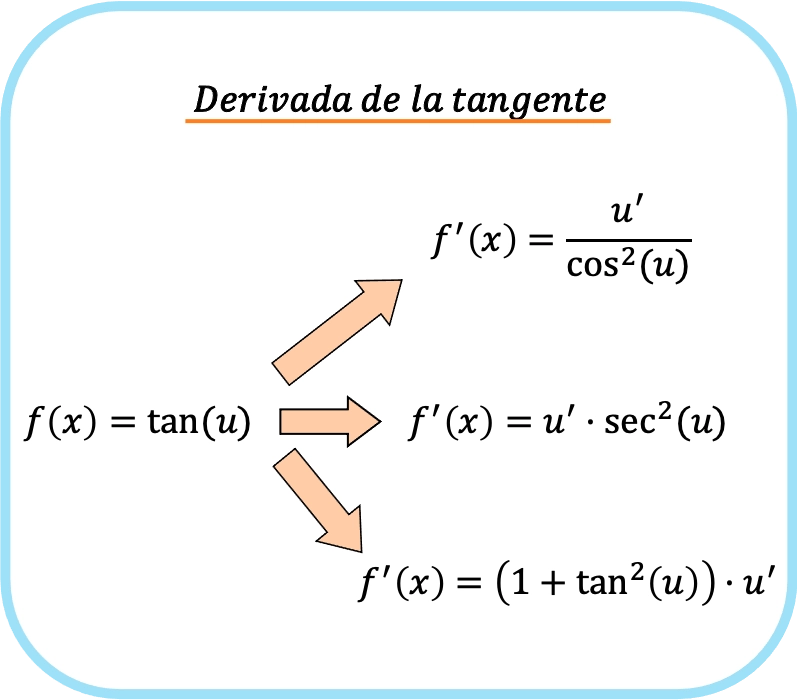
من ناحية أخرى، عندما يكون لدينا في وسيطة الظل دالة مختلفة عن x (دعنا نسميها u)، يجب علينا تطبيق قاعدة السلسلة. لذلك فإن مشتق ظل u هو:

$\begin{array}{c}f(x)=\text{tan}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cos}^2(u)}=\text{sec}^2(u)\cdot u'=\left(1+\text{tan}^2(u)\right)\cdot u'\end{array}$

وباختصار، يمكن تلخيص قاعدة مشتقة الظل على النحو التالي:

أمثلة على مشتقات الظل

بالنظر إلى صيغة مشتقة الظل، سنحل في هذا القسم عدة أمثلة لهذا النوع من المشتقات المثلثية حتى تفهم كيفية اشتقاق دالة الظل.

مثال 1: مشتقة ظل 2x

$f(x)=\text{tan}(2x)$

لحساب مشتقة المماس، يمكنك استخدام إحدى الصيغ الثلاث التي رأيناها أعلاه. في هذه الحالة، سوف نستخدم صيغة جيب التمام:

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

الدالة 2x خطية، لذا فإن مشتقتها هي 2. لذا فإن مشتق ظل 2x هو 2 على مربع جيب تمام 2x:

$f(x)=\text{tan}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\text{cos}^2(2x)}$

مثال 2: مشتقة ظل x تربيع

$f(x)=\text{tan}(x^2)$

في هذا المثال، دالة وسيطة الظل ليست x، ولكنها دالة بمشتقة. وهو ما يعني أننا بحاجة إلى تطبيق قاعدة السلسلة لاشتقاقها.

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

مشتقة x تربيع هي 2x، لذا فإن مشتقة ظل x ² هي:

$f(x)=\text{tan}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\text{cos}^2(x^2)}$

مثال 3: مشتقة مماس المكعب

$f(x)=\text{tan}^3(9x^2-4x)$

في هذه المسألة لدينا دالة مركبة، لذا سنحتاج أيضًا إلى استخدام قاعدة السلسلة لاشتقاق المماس.

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

بالإضافة إلى ذلك، يتم رفع الظل إلى القوة 3، مما يعني أنه قبل تطبيق صيغة مشتقة الظل، يجب عليك استخدام صيغة مشتقة القوة:

$\begin{aligned}f'(x)&=3\text{tan}^2(9x^2-4x)\cdot \cfrac{18x-4}{\text{cos}^2(9x^2-4x)} \\[2ex]&=\cfrac{3\text{tan}^2(9x^2-4x)\cdot(18x-4)}{\text{cos}^2(9x^2-4x)}\end{aligned}$

مشتق من الظل العكسي

مثل أي دالة عكسية، فإن دالة الظل لها أيضًا معكوس، وهي دالة ظل قوسية. على الرغم من أن صيغة اشتقاقها ليست مشابهة لصيغة الظل، إلا أننا نعرضها لك لأنها يمكن أن تكون مفيدة في بعض الحالات.

مشتقة المماس العكسي للدالة هي حاصل قسمة مشتقة الدالة على واحد زائد تربيع الدالة المذكورة

$f(x)=\text{tan}^{-1}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

على سبيل المثال، مشتقة المماس العكسي لـ 3x هي:

$f(x)=\text{tan}^{-1}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3}{1+(3x)^2}=\cfrac{3}{1+9x^2}$

تمارين محلولة على مشتقة المماس

احسب مشتقة دوال الظل التالية:

$\text{A) } f(x)=\text{tan}(3x)$

$\text{B) } f(x)=\text{tan}(x^3-10x^2+8)$

$\text{C) } \displaystyle f(x)=\text{tan}^2\left(\frac{x}{2}\right)$

$\text{D) } f(x)=\text{tan}\left(e^{2x}\right)$

$\text{E) } f(x)=\text{tan}\bigl(\ln(4x)\bigr)$

$\text{F) } f(x)=\text{tan}\left(\sqrt{3x}\right)$

انظر الحل

$\text{A) } f'(x)=\cfrac{3}{\text{cos}^2(3x)}$

$\text{B) } f'(x)=\cfrac{3x^2-20x}{\text{cos}^2(x^3-10x^2+8)}$

$\text{C) } \displaystyle f'(x)=2\text{tan}\left(\frac{x}{2}\right)\cdot \frac{1}{\text{cos}^2\left(\frac{x}{2}\right)}\cdot \frac{1}{2}=\frac{\text{tan}\left(\frac{x}{2}\right)}{\text{cos}^2\left(\frac{x}{2}\right)}$

$\text{D) } f'(x)=\cfrac{2e^{2x}}{\text{cos}^2(e^{2x})}$

$\text{E) } f'(x)=\cfrac{\frac{4}{4x}}{\text{cos}^2\bigl(\ln(4x)\bigr)}=\cfrac{1}{x\cdot\text{cos}^2\bigl(\ln(4x)\bigr)}$

$\text{F) } f'(x)=\cfrac{\frac{3}{2\sqrt{3x}}}{\text{cos}^2\left(\sqrt{3x}\right)}=\cfrac{3}{2\sqrt{3x}\cdot \text{cos}^2\left(\sqrt{3x}\right)}$

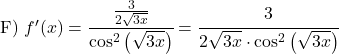
إثبات مشتقة الظل

لكي تتمكن من التحقق من أن هذا ليس تعبيرًا مبتكرًا، سنوضح في هذا القسم صيغة مشتقة الظل باستخدام التعريف الرياضي للظل.

وللقيام بذلك سنبدأ من الهوية المثلثية التي تربط بين النسب المثلثية الثلاث:

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}$

إذا استخدمنا صيغة مشتقة القسمة ، فإن المشتقة ستكون:

$\displaystyle\left(\text{tan}(x)\right)'=\left(\frac{\text{sen}(x)}{\text{cos}(x)}\right)'$

$\text{tan}'(x)=\cfrac{\text{cos}(x)\cdot \text{cos}(x)+\text{sen}(x)\text{sen}(x) }{\text{cos}^2(x)}$

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)+\text{sen}^2(x)}{\text{cos}^2(x)}$

لكن، باستخدام الهوية المثلثية الأساسية، نعلم أن مربع جيب التمام بالإضافة إلى مربع جيب التمام هو 1:

$\text{sen}^2(x)+\text{cos}^2(x)=1$

$\text{tan}'(x)=\cfrac{1}{\text{cos}^2(x)}$

وبذلك نكون قد توصلنا بالفعل إلى الصيغة الأولى لمشتقة المماس. علاوة على ذلك، فإن القاطع هو المعكوس المضاعف لجيب التمام، لذلك يتم اشتقاق التعبير الثاني أيضًا:

$\text{tan}'(x)=\text{sec}^2(x)$

وأخيرًا، يمكن إثبات القاعدة الثالثة للمشتقة الظلية بتحويل الكسر من الخطوة السابقة إلى مجموع الكسور:

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)+\text{sen}^2(x)}{\text{cos}^2(x)}$

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)}{\text{cos}^2(x)}+\cfrac{\text{sen}^2(x)}{\text{cos}^2(x)}$

$\text{tan}'(x)=1+\text{tan}^2(x)$

ما هو مشتق الظل؟

أمثلة على مشتقات الظل

مثال 1: مشتقة ظل 2x

مثال 2: مشتقة ظل x تربيع

مثال 3: مشتقة مماس المكعب

مشتق من الظل العكسي

تمارين محلولة على مشتقة المماس

إثبات مشتقة الظل

اترك تعليقاً إلغاء الرد