مصفوفة قطرية

في هذه الصفحة سترى ما هي المصفوفة القطرية وأمثلة على المصفوفات القطرية. بالإضافة إلى ذلك، سوف تكتشف كيفية التعامل مع هذا النوع من المصفوفات، وكيفية حساب محدداتها بسهولة وكيفية عكسها. هناك أيضًا خصائص وتطبيقات للمصفوفات القطرية. وأخيرًا، هناك تفسيرات للمصفوفة ثنائية القطر والمصفوفة ثلاثية الأقطار.

ما هي المصفوفة القطرية؟

المصفوفة القطرية هي مصفوفة مربعة تكون فيها جميع العناصر غير الموجودة على القطر الرئيسي صفر (0). قد تكون أو لا تكون عناصر القطر الرئيسي صفرًا.

بمجرد أن نعرف التعريف الدقيق للمصفوفة القطرية، سنرى أمثلة على المصفوفات القطرية:

أمثلة على المصفوفات القطرية

مثال لمصفوفة قطرية البعد 2 × 2

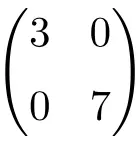
مثال لمصفوفة قطرية من الرتبة 3×3

مثال لمصفوفة قطرية بحجم 4×4

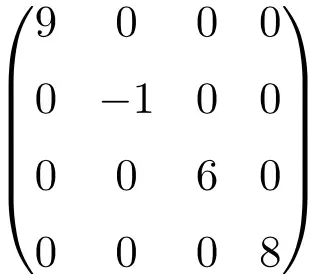
تتم كتابة هذه الأنواع من المصفوفات عمومًا للإشارة إلى عناصر القطر:

$diag(2,5,1) = \left. \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

العمليات مع المصفوفات القطرية

أحد أسباب أهمية المصفوفات القطرية في الجبر الخطي هو السهولة التي تتيح لك إجراء العمليات الحسابية. ولهذا السبب يتم استخدامها كثيرًا في الرياضيات.

جمع وطرح المصفوفات القطرية

إن إضافة (وطرح) مصفوفتين قطريتين أمر بسيط للغاية: ما عليك سوى إضافة (أو طرح) الأرقام الموجودة على القطرين.

$\displaystyle \text{diag}(a_1,... ,a_n) \pm \text{diag}(b_1 ,... , b_n) = \text{diag}(a_1\pm b_1,..., a_n\pm b_n)$

على سبيل المثال:

$\displaystyle \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} +\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -4 \end{pmatrix} = \begin{pmatrix} 6& 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}$

ضرب المصفوفة القطرية

لحل ناتج الضرب أو المصفوفة لمصفوفتين قطريتين، ما عليك سوى ضرب عناصر القطرين معًا.

$\displaystyle \text{diag}(a_1,... ,a_n) \cdot \text{diag}(b_1 ,... , b_n) = \text{diag}(a_1\cdot b_1,..., a_n\cdot b_n)$

على سبيل المثال:

$\displaystyle \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & -4 & 0 \\[1.1ex] 0 & 0 & -3 \end{pmatrix} \cdot\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} = \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -18 \end{pmatrix}$

قوة المصفوفات القطرية

لحساب قوة مصفوفة قطرية، نحتاج إلى رفع كل عنصر من عناصر القطر إلى الأس:

$\displaystyle A= \text{diag}(a_1,... ,a_n)$

$\displaystyle A^k= \text{diag}(a_1^k,... ,a_n^k)$

على سبيل المثال:

$\displaystyle\left. \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}\right.^3= \begin{pmatrix} 27 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & 64 \end{pmatrix}$

محدد مصفوفة قطرية

محدد المصفوفة القطرية هو حاصل ضرب العناصر الموجودة على القطر الرئيسي.

$\displaystyle A= \text{diag}(a_1,... ,a_n)$

$\displaystyle \text{det}(A)= \prod_{i =1}^n a_i$

انظر إلى التمرين التالي الذي تم حله والذي نجد فيه محدد المصفوفة القطرية ببساطة عن طريق ضرب عناصر قطرها الرئيسي:

$\displaystyle \begin{vmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 5 \cdot 2 \cdot 3 = 30$

من السهل إثبات هذه النظرية: ما عليك سوى حساب محدد المصفوفة القطرية بواسطة الكتل (أو العوامل المساعدة). تم تفصيل هذا العرض التوضيحي أدناه باستخدام مصفوفة قطرية عامة:

$\begin{aligned} \begin{vmatrix} a & 0 & 0 \\[1.1ex] 0 & b & 0 \\[1.1ex] 0 & 0 & c \end{vmatrix}& = a \cdot \begin{vmatrix} b & 0 \\[1.1ex] 0 & c \end{vmatrix} - 0 \cdot \begin{vmatrix} 0 & 0 \\[1.1ex] 0 & c \end{vmatrix} + 0 \cdot \begin{vmatrix} 0 & b \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (b\cdot c) - 0 \cdot 0 + 0 \cdot 0 \\[2ex] & = a \cdot b \cdot c \end{aligned}$

عكس مصفوفة قطرية

تكون المصفوفة القطرية قابلة للعكس إذا وفقط إذا كانت جميع عناصر القطر الرئيسي مختلفة عن 0 . وفي هذه الحالة نقول أن المصفوفة القطرية هي مصفوفة منتظمة.

بالإضافة إلى ذلك، فإن معكوس المصفوفة القطرية سيكون دائمًا مصفوفة قطرية أخرى مع معكوسات القطر الرئيسي:

$\displaystyle A= \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 8 \end{pmatrix} \ \longrightarrow \ A^{-1}=\begin{pmatrix} \frac{1}{3} & 0 & 0 \\[1.1ex] 0 & \frac{1}{2} & 0 \\[1.1ex] 0 & 0 & \frac{1}{8} \end{pmatrix}$

ومن الخاصية السابقة يمكننا أن نستنتج أن محدد معكوس المصفوفة القطرية هو حاصل ضرب معكوس القطر الرئيسي:

$\displaystyle B= \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & -1 \end{pmatrix}$

$\displaystyle\left| B^{-1}\right|=\cfrac{1}{2} \cdot \cfrac{1}{4} \cdot \cfrac{1}{-1}=-\cfrac{1}{8} = -0,125$

خصائص المصفوفات القطرية

أي مصفوفة قطرية هي أيضًامصفوفة متماثلة .

المصفوفة القطرية هيمصفوفة ذات شكل مثلث علوي وسفلي .

مصفوفة الهوية هي مصفوفة قطرية:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

وبالمثل، فإن المصفوفة الصفرية هي أيضًا مصفوفة قطرية، لأن جميع عناصرها التي ليست على القطر هي أصفار. على الرغم من أن الأرقام الموجودة على القطر هي 0.

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

القيم الذاتية (أو القيم الذاتية) للمصفوفة القطرية هي عناصر قطرها الرئيسي.

$\begin{pmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix} \longrightarrow \ \lambda = 3 \ ; \ \lambda = 4 \ ; \ \lambda = 7$

تكون المصفوفة المربعة قطرية إذا وفقط إذا كانت مثلثة وطبيعية .

المصفوفة المجاورة للمصفوفة القطرية هي مصفوفة قطرية أخرى.

تطبيقات المصفوفة القطرية

كما رأينا، فإن حل العمليات الحسابية باستخدام المصفوفات القطرية أمر بسيط للغاية، لأن العديد من الأصفار تشارك في العمليات. ولهذا السبب، فهي مفيدة جدًا في مجال الرياضيات وتستخدم على نطاق واسع.

لهذا السبب نفسه، تم إجراء العديد من الدراسات حول كيفية جعل المصفوفة قطريًا ، وفي الواقع، تم تطوير طريقة لقطر المصفوفات (باستخدام متعدد الحدود المميز).

ولذلك، فإن المصفوفات القابلة للتخصيص ذات أهمية كبيرة أيضًا. مثل نظرية التحلل الطيفي، التي تحدد الشروط التي تحدد متى يمكن أن تكون المصفوفة قطرية ومتى لا تكون كذلك.

مصفوفة ثنائية القطر

المصفوفة ثنائية القطر هي مصفوفة مربعة تكون فيها جميع العناصر التي ليست على القطر الرئيسي أو على القطر العلوي أو السفلي 0.

على سبيل المثال:

$\begin{pmatrix} 3 & 2 & 0 \\[1.1ex] 0 & -5 & 1 \\[1.1ex] 0 & 0 & 6 \end{pmatrix}$

مصفوفة ثنائية القطر العلوي

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 0 & 7 & 4 \end{pmatrix}$

مصفوفة ثنائية القطر السفلية

عندما يكون القطر الرئيسي والقطري الفائق مشغولين، فإننا نتحدث عن مصفوفة ثنائية القطر العلوية. من ناحية أخرى، عندما يكون القطر الرئيسي والقطر الفرعي الأول مشغولين، فإننا نتحدث عن مصفوفة ثنائية القطر أقل.

مصفوفة ثلاثية الأقطار

المصفوفة ثلاثية الأقطار هي مصفوفة مربعة عناصرها الوحيدة غير الصفرية هي عناصر القطر الرئيسي والأقطار المجاورة في الأعلى والأسفل.

على سبيل المثال:

$\begin{pmatrix} 2 & 3 & 0 & 0 \\[1.1ex] -4 & 5 & 9 & 0 \\[1.1ex] 0 & 1 & 6 & -2 \\[1.1ex] 0 & 0 & 8 & 7 \end{pmatrix}$

وبالتالي، فإن جميع المصفوفات القطرية والثنائية والثلاثية هي أمثلة على المصفوفات الشريطية . لأن المصفوفة الشريطية هي تلك المصفوفة التي تحتوي على جميع عناصرها غير الصفرية حول القطر الرئيسي.

ما هي المصفوفة القطرية؟

أمثلة على المصفوفات القطرية

العمليات مع المصفوفات القطرية

جمع وطرح المصفوفات القطرية

ضرب المصفوفة القطرية

قوة المصفوفات القطرية

محدد مصفوفة قطرية

عكس مصفوفة قطرية

خصائص المصفوفات القطرية

تطبيقات المصفوفة القطرية

مصفوفة ثنائية القطر

مصفوفة ثلاثية الأقطار

اترك تعليقاً إلغاء الرد