خواص المحددات - الماثوريتي

في هذا القسم، سنرى ما هي جميع خصائص المحددات . نعرض أيضًا كل خاصية بمثال حتى تتمكن من فهمها بالكامل. بالإضافة إلى ذلك، ستجد تمارين تتعلق بخصائص المحددات.

سنشرح أدناه كل خاصية من خصائص المحددات واحدة تلو الأخرى، ولكن إذا كنت تفضل ذلك، يمكنك الانتقال مباشرة إلى الجدول الملخص أدناه. 😉

الخاصية 1: محدد المصفوفة المنقولة

محدد المصفوفة يعادل محدد المصفوفة المنقولة.

$\lvert A \rvert = \lvert A^t \rvert$

مثال:

$\lvert A \rvert = \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot 3 = 10 - 3 = \bm{7}$

الآن نقوم بتبديل المصفوفة 2×2 ونحل قيمة المحدد. لاحظ أننا حصلنا على نفس النتيجة السابقة:

$\lvert A^t \rvert = \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & 5 \end{vmatrix} = 2 \cdot 5 - 3 \cdot 1 = 10 - 3 = \bm{7}$

الخاصية 2: محدد يحتوي على صف أو عمود مملوء بالأصفار

إذا كان للمحدد صف أو عمود مملوء بالأصفار، فسيرجع المحدد 0.

$\displaystyle \begin{vmatrix} a_{11} & 0 & a_{13} \\[1.1ex] a_{21} & 0 & a_{23} \\[1.1ex] a_{31} & 0 & a_{33}\end{vmatrix}=0$

مثال:

$\begin{vmatrix} 5 & 6 & 2 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] -3 & 1 & 4 \end{vmatrix} = \bm{0} \qquad \qquad \begin{vmatrix} 1 & -5 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 1 & 3 & 0 \end{vmatrix} = \bm{0}$

في كلا المثالين، قيمة المحددات هي 0. لأن الصف الثاني من المحدد الأول به أصفار بالكامل والعمود الثالث من المحدد الثاني به أصفار أيضًا.

الخاصية الثالثة: المحدد ذو صفين أو عمودين متساويين

إذا كان للمحدد صفين أو عمودين متساويين أو متعددين، يكون المحدد صفر (0).

لذلك، إذا كان هناك مجموعة خطية بين الصفوف أو الأعمدة، أي أنها تعتمد خطيًا، فإن المحدد يعطي 0.

مثال:

$\begin{vmatrix} 3 & 4 & 4 \\[1.1ex] -1 & 5 & 5 \\[1.1ex] 6 & 2 & 2 \end{vmatrix} = 0$

في هذه الحالة، يعطي المحدد 0 لأن العمودين 2 و 3 متساويان.

الخاصية 4: تعديل صفوف أو أعمدة المحدد

إذا تم تعديل صفين أو عمودين بالنسبة لبعضهما البعض، فإن المحدد يعطي نفس النتيجة ولكن بإشارة مختلفة.

$\displaystyle \begin{vmatrix} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{vmatrix}= - \begin{vmatrix} a & c & b \\[1.1ex] d & f & e \\[1.1ex] g & i & h \end{vmatrix}$

مثال:

$\begin{vmatrix} 3 & 2 & -4 \\[1.1ex] 1 & 5 & 6 \\[1.1ex] 1 & 0 & -3 \end{vmatrix} = \displaystyle -45 +12+0+20-0+6= \bm{-7}$

الآن نقوم بتغيير ترتيب العمودين 2 و 3 بالنسبة لبعضهما البعض. لاحظ أن النتيجة هي نفسها ولكن بعلامة مختلفة:

$\begin{vmatrix} 3 & -4 & 2 \\[1.1ex] 1 & 6 & 5 \\[1.1ex] 1 & -3 & 0 \end{vmatrix} = \displaystyle 0-20-6-12+45-0= \bm{+7}$

الخاصية 5: ضرب صف من المحددات في عدد قياسي

إن ضرب جميع العناصر الموجودة في صف أو عمود بأكمله في رقم حقيقي هو نفس ضرب نتيجة المحدد في هذا الرقم.

$\displaystyle \begin{vmatrix} k \cdot a_{11} & k \cdot a_{12} & k \cdot a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}$

$\displaystyle \begin{vmatrix} k \cdot a_{11} & a_{12} & a_{13} \\[1.1ex] k \cdot a_{21} & a_{22} & a_{23} \\[1.1ex] k \cdot a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}$

مثال:

$\displaystyle \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-3= \bm{5}$

الآن نأخذ نفس المحدد ونضرب سطرًا كاملاً في 2. سترى أن النتيجة ستكون نتيجة المحدد السابق ولكن مضروبة في 2 أو 10:

$\displaystyle \begin{vmatrix} 2 \cdot 2 & 2 \cdot 3 \\[1.1ex] 1 & 4 \end{vmatrix} = \begin{vmatrix} 4 & 6 \\[1.1ex] 1 & 4 \end{vmatrix} = 16-6 =\bm{10}$

الخاصية 6: محدد منتج المصفوفة

محدد حاصل ضرب مصفوفتين يساوي حاصل ضرب محدد كل مصفوفة على حدة.

$\displaystyle \lvert A \cdot B \rvert = \lvert A \rvert \cdot \lvert B \rvert$

مثال:

لتوضيح خاصية المحددات هذه، سنحسب محدد ضرب المصفوفتين التاليتين بطريقتين محتملتين:

$\displaystyle A= \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix}\quad B=\begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}$

سنقوم أولًا بضرب المصفوفتين، ثم نحسب محدد المصفوفة الناتجة:

$\displaystyle \left| A \cdot B \right| =\left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = \left| \begin{pmatrix} 7 & -1 \\[1.1ex] 13 & -1 \end{pmatrix} \right| = -7 - (-13) = \bm{6}$

الآن نحسب محدد كل مصفوفة على حدة ثم نضرب النتائج:

$\displaystyle \lvert A \rvert \cdot \lvert B \rvert = \left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = -1\cdot (-6)= \bm{6}$

كما ترون، فإن حساب حاصل ضرب المصفوفة أولًا ثم المحدد يعطي نفس النتيجة مثل حساب محدد كل مصفوفة أولًا ثم ضرب النتائج.

ومن ناحية أخرى، لا ينطبق هذا الشرط على عمليات الجمع والطرح، أي أن محدد الجمع (أو الطرح) لمصفوفتين لا يعطي نفس نتيجة الجمع (أو الطرح) لمحددات العدد مصفوفتين بشكل منفصل.

الخاصية 7: محدد المصفوفة العكسية

إذا كانت المصفوفة قابلة للعكس، فإن محدد معكوسها يتوافق مع معكوس محدد المصفوفة الأصلية.

$\displaystyle \begin{vmatrix} A^{-1} \end{vmatrix} = \cfrac{1}{\lvert A \rvert}$

مثال:

سوف نتحقق من هذه الخاصية عن طريق حساب معكوس المصفوفة أولًا ثم إيجاد قيمة محددها. سنرى أن النتيجة تعادل إيجاد محدد المصفوفة الأصلية وعكسها.

لذلك نعكس المصفوفة التالية ونحسب محددها:

$\displaystyle A= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}$

$\displaystyle A^{-1}= \begin{pmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{pmatrix}$

$\displaystyle \begin{vmatrix}A^{-1} \end{vmatrix}= \begin{vmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{vmatrix} = 4-\cfrac{7}{2} =\cfrac{8}{2}-\cfrac{7}{2} = \cfrac{\bm{1}}{\bm{2}}$

والآن نحل قيمة محدد المصفوفة الأصلية ونقوم بعكسها:

$\displaystyle \begin{vmatrix}A\end{vmatrix}= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}=16-14=2$

$\displaystyle \begin{vmatrix}A^{-1}\end{vmatrix}= \cfrac{\bm{1}}{\bm{2}}$

وكما ترون فإن نتائج كلتا العمليتين متطابقة. وبالتالي يتم إثبات الملكية.

الخاصية 8: استبدال سطر المحدد

يمكن استبدال صف المحدد بإضافة (أو طرح) نفس الصف بالإضافة إلى (أو ناقص) صف آخر مضروبًا في رقم.

مثال:

مع المثال التالي سوف نتحقق من هذه الخاصية. سنقوم أولاً بحساب المحدد، ثم سنعمل على صف من المحدد ونعيد حساب نتيجته. سترى كيف حصلنا على نفس النتيجة في كلتا الحالتين.

لذا، دعونا أولاً نحسب المحدد 3×3 باستخدام قاعدة ساروس:

$\begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \displaystyle=0+0+9-0+6-18 = \bm{-3}$

الآن، في السطر 2، نضيف السطر الأول مضروبًا في 2:

$\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \begin{matrix} \\[1.1ex] \xrightarrow{f_2 + 2f_1} \\[1.1ex] \ \end{matrix} \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix}$

ونحل المحدد بعد تحويل أحد خطوطه:

$\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} = 24+0+21-0-6-42=\bm{-3}$

وفي كلتا الحالتين كانت النتيجة -3. وهكذا يتبين أن نتيجة المحدد لا تتغير إذا تم استبدال صف بمجموع نفس الصف بالإضافة إلى صف آخر مضروبا في رقم.

الخاصية 9: محدد المصفوفة المثلثية

محدد المصفوفة المثلثية هو حاصل ضرب عناصر قطرها الرئيسي.

مثال:

سوف نقوم بحل محدد المصفوفة المثلثية التالية كمثال:

$\begin{vmatrix} 2 & 3 & 5 \\[1.1ex] 0 & -1 & 7 \\[1.1ex] 0 & 0 & 4 \end{vmatrix} \displaystyle= 2 \cdot (-1) \cdot 4 = \bm{-8}$

الخاصية 10: محدد المصفوفة القطرية

محدد المصفوفة القطرية يساوي ضرب عناصر قطرها الرئيسي.

مثال:

لنأخذ على سبيل المثال محدد المصفوفة القطرية التالية:

$\begin{vmatrix}5 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -2 \end{vmatrix} \displaystyle= 5 \cdot 3 \cdot (-2) = \bm{-30}$

جدول ملخص لخصائص المحددات

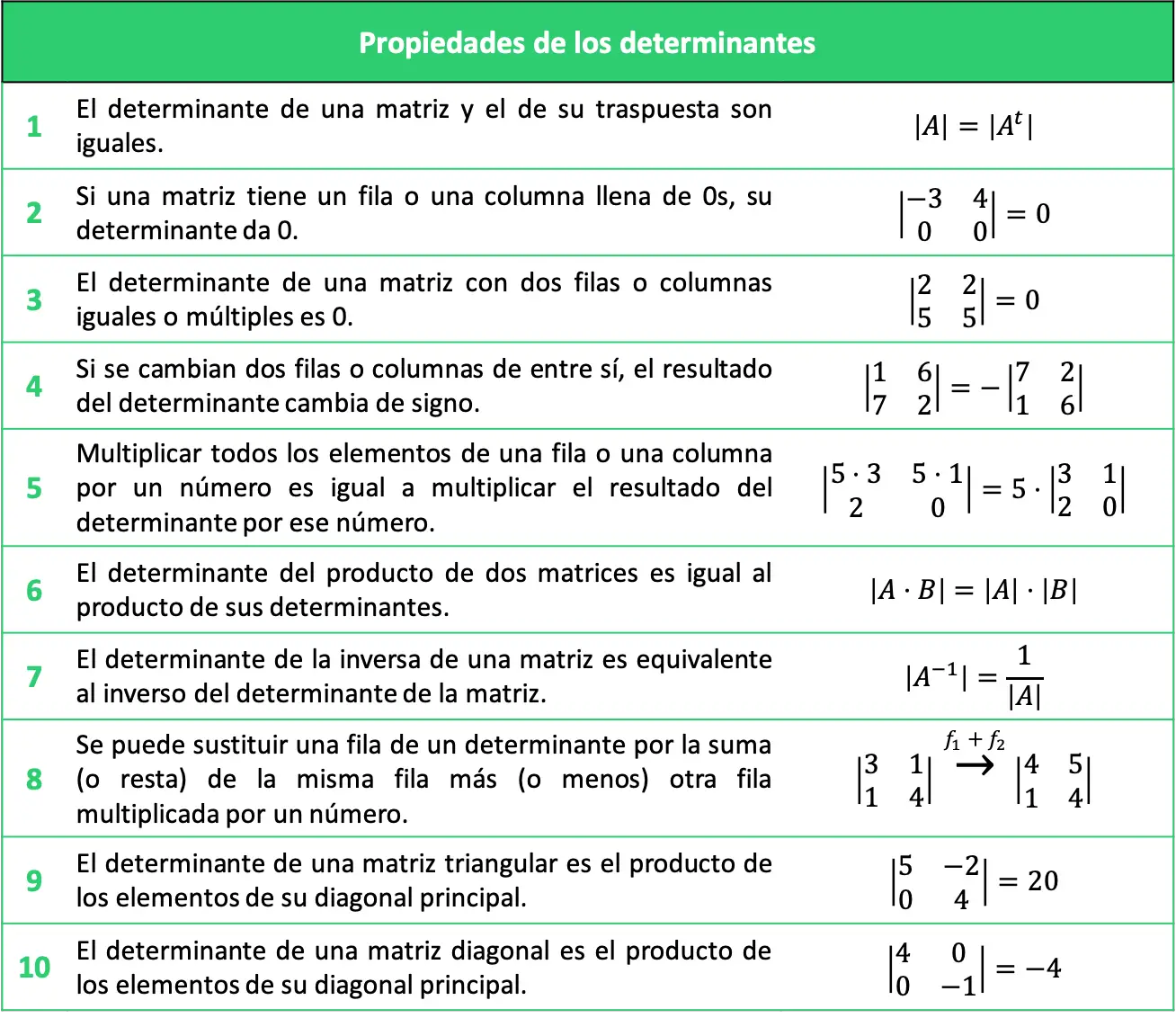
ويمكن تلخيص خصائص المحددات الموضحة في الجدول التالي:

تمارين محلولة مع خواص المحددات

التمرين 1

حل المحدد التالي:

$\displaystyle \begin{vmatrix} 3 & 1 & 0 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -1 & 6 & 0 \end{vmatrix}$

انظر الحل

إذا كان للمحدد صف أو عمود مملوء بالأصفار، فسيرجع المحدد 0 (الخاصية 2). وبالتالي فإن نتيجة المحدد هي 0، لأن العمود الثالث مملوء بالأصفار.

تمرين 2

حل المحدد التالي:

$\displaystyle \begin{vmatrix} 4 & 2 & -3 & 5 \\[1.1ex] 1 & 5 & 3 & 2 \\[1.1ex]4 & 2 & -3 & 5 \\[1.1ex] -2 & 0 & 4 & 3 \end{vmatrix}$

انظر الحل

إذا كان للمحدد صفين أو عمودين متساويين أو متعددين، فسيرجع المحدد 0 (الخاصية 3). وبالتالي فإن نتيجة المحدد هي 0، لأن الصف الأول والصف الثالث متساويان.

التمرين 3

احسب المحدد التالي:

$\displaystyle \begin{vmatrix} 1 & 0 & 2 & 2 \\[1.1ex] 3 & 1 & 5 & 6 \\[1.1ex] 1 & 3 & -2 & 2 \\[1.1ex] 2 & 2 & 0 & 4 \end{vmatrix}$

انظر الحل

إذا كان للمحدد صفين أو عمودين متساويين أو متعددين، فسيرجع المحدد 0 (الخاصية 3). ولذلك فإن نتيجة المحدد هي 0، لأن العمود الرابع هو ضعف العمود الأول.

التمرين 4

نحن نعرف نتيجة المحدد، على الرغم من أننا لا نعرف عناصر المصفوفة:

$\displaystyle \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} = 3$

من نتيجة المحدد السابق وخواص المحددات احسب نتيجة المحددات التالية:

$\displaystyle \mathbf{a} \bm{)} \ \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix} \qquad \mathbf{b} \bm{)} \ \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} \qquad \mathbf{c} \bm{)} \ \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix}$

انظر الحل

ل)

$\begin{pmatrix} a & c \\ b & d \end{pmatrix}$

هي المصفوفة المنقولة

$\begin{pmatrix} a & b \\ c & d \end{pmatrix}$

. ومحدد المصفوفة يساوي محدد المصفوفة المنقولة (الخاصية 1). ولذلك فإن نتيجة هذا المحدد هي أيضا 3.

$\displaystyle \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix}=\begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}=\bm{3}$

ب) في التحديد

$\begin{vmatrix} b & a \\ d & c \end{vmatrix}$

تم تعديل العمودين 1 و2 فيما يتعلق بمحدد العبارة

$\begin{vmatrix} a & b \\ c & d \end{vmatrix}$

. ولذلك، وفقا للخاصية 4، فإن النتيجة هي نفس نتيجة محدد العبارة ولكن بإشارة مختلفة، أي -3.

$\displaystyle \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} = - \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}= \bm{-3}$

ج) في التحديد

$\begin{vmatrix} a & 3b \\ c & 3d \end{vmatrix}$

لقد تم ضرب العمود الثاني بأكمله من محدد العبارة في 3. لذلك من الخاصية 5 يمكننا أن نستنتج أن نتيجتها ستكون أيضًا نتيجة محدد العبارة مضروبًا في 3، أي 9.

$\displaystyle \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix} =3 \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} =3 \cdot 3 = \bm{9}$

التمرين 5

نحن نعرف نتيجة هذين المحددين:

$\displaystyle\vert A \vert = \begin{vmatrix} 1 & 2 & 0 & 1 \\[1.1ex] -2 & -1 & 1 & 0 \\[1.1ex] 1 & 3 & 3 & -1 \\[1.1ex] 3 & 4 & 1 & 1 \end{vmatrix}=8$

$\displaystyle\vert B \vert = \begin{vmatrix} 0 & 1 & 3 & 2 \\[1.1ex] -1 & -2 & 0 & 0 \\[1.1ex] 3 & 1 & 1 & 2 \\[1.1ex] -1 & 2 & 3 & 1 \end{vmatrix} = - 4$

من هذه المعلومات احسب:

$\displaystyle \vert A \cdot B \vert$

انظر الحل

لحساب نتيجة المحدد، ليس من الضروري ضرب المصفوفات 4×4. حيث أن محدد حاصل ضرب مصفوفتين يساوي حاصل ضرب محدد كل مصفوفة على حدة (الخاصية 6). حتى الآن:

$\vert A \cdot B \vert = \vert A \vert \cdot \vert B \vert = 8 \cdot (-4) = \bm{-32}$

الخاصية 1: محدد المصفوفة المنقولة

مثال:

الخاصية 2: محدد يحتوي على صف أو عمود مملوء بالأصفار

مثال:

الخاصية الثالثة: المحدد ذو صفين أو عمودين متساويين

مثال:

الخاصية 4: تعديل صفوف أو أعمدة المحدد

مثال:

الخاصية 5: ضرب صف من المحددات في عدد قياسي

مثال:

الخاصية 6: محدد منتج المصفوفة

مثال:

الخاصية 7: محدد المصفوفة العكسية

مثال:

الخاصية 8: استبدال سطر المحدد

مثال:

الخاصية 9: محدد المصفوفة المثلثية

مثال:

الخاصية 10: محدد المصفوفة القطرية

مثال:

جدول ملخص لخصائص المحددات

تمارين محلولة مع خواص المحددات

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

اترك تعليقاً إلغاء الرد