في هذه الصفحة سوف تتعلم ما هو محدد المصفوفة المربعة 3×3. سترى كيفية حل محددات الترتيب 3 باستخدام قاعدة ساروس. وبالإضافة إلى ذلك، لديك أمثلة وتمارين تم حلها خطوة بخطوة، حتى تتمكن من التدرب عليها وفهمها بشكل مثالي.
ما هو محدد المصفوفة 3×3؟
محدد الرتبة 3 هو مصفوفة البعد 3×3 ممثلة بشريط رأسي على كل جانب من المصفوفة. على سبيل المثال، إذا كان لدينا المصفوفة التالية:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 2 & 0 & 4 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 1 & 6 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7b5e89b706893e88dd15882e3685afb1_l3.png)
يتم تمثيل محدد المصفوفة A على النحو التالي:
![Rendered by QuickLaTeX.com \displaystyle \lvert A \rvert = \begin{vmatrix} 2 & 0 & 4 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 1 & 6 & -2 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41db04327de87a80f1e0e4dd6dcb220a_l3.png)
كما رأيت، فإن كتابة محدد مصفوفة مربعة من الرتبة 3 أمر سهل. الآن دعونا نرى كيفية حلها:
كيفية حساب محدد الطلب 3؟
لإنشاء محددات المصفوفات 3×3 عليك تطبيق قاعدة ساروس :
حكم ساروس
تنص قاعدة ساروس على أنه لحساب محدد الرتبة 3، يجب أن نجمع حاصل ضرب عناصر القطر الأكبر وحاصل أقطاره المتوازية مع رءوسها المقابلة المقابلة، ثم نطرح حاصل ضرب عناصر القطر الأصغر و حاصل ضرب قطريها المتوازيين في رءوسهما المقابلة لها.
إذا تمت كتابتها بهذه الطريقة، فقد يكون من الصعب فهمها بعض الشيء، ولكن انظر إلى كيفية إجراء حساب محددات 3×3 باستخدام الرسم البياني والأمثلة التالية:


أمثلة على محددات 3×3:
![Rendered by QuickLaTeX.com \begin{aligned} \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] -1 & 1 & 0 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} & = 2 \cdot 1 \cdot 1 + 1 \cdot 0 \cdot (-2) + (-1) \cdot 4 \cdot 3 - (-2) \cdot 1 \cdot 3 - 4 \cdot 0 \cdot 2- (-1) \cdot 1 \cdot 1 \\ & = 2 + 0 -12 +6 - 0 +1 \\[2ex] & = \bm{-3} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-98e60cf465cd0eb7662d47770cd38231_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} \begin{vmatrix} 1 & 0 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 4 & -3 & -1 \end{vmatrix} & = 1\cdot 2 \cdot (-1) + 0 \cdot 1 \cdot 4 +3 \cdot (-3) \cdot 2 - 4 \cdot 2 \cdot 2 - (-3) \cdot 1 \cdot 1- 3 \cdot 0 \cdot (-1) \\ & = -2 +0 -18 - 16 +3- 0 \\[2ex] & = \bm{-33} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41a53c1fd6eae1b51a280a6ce1e2ab91_l3.png)
حل مسائل محددات المصفوفات 3 × 3
التمرين 1
حل المحدد 3×3 التالي:
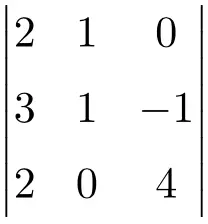
لحل محدد مصفوفة 3×3 يجب علينا تطبيق قاعدة ساروس:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 2 & 1 & 0 \\[1.1ex] 3 & 1 & -1 \\[1.1ex] 2 & 0 & 4 \end{vmatrix} & = 2 \cdot 1 \cdot 4 + 1 \cdot (-1) \cdot 2 + 3 \cdot 0 \cdot 0 - 2 \cdot 1 \cdot 0 - 0 \cdot (-1) \cdot 2- 3 \cdot 1 \cdot 4 \\ & = 8 -2 +0 -0- 0-12 \\[2ex] & = \bm{-6} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8f288312b72f3bbabc35ee64bf580d8c_l3.png)
تمرين 2
احسب المحدد التالي للترتيب 3:
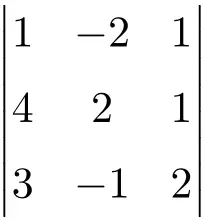
لحساب محدد مصفوفة من الدرجة الثالثة، يجب علينا استخدام قاعدة ساروس:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 1 & -2 & 1 \\[1.1ex] 4 & 2 & 1 \\[1.1ex] 3 & -1 & 2 \end{vmatrix} & = 1 \cdot 2 \cdot 2 + (-2) \cdot 1 \cdot 3 + 4 \cdot (-1) \cdot 1 - 3 \cdot 2 \cdot 1 - (-1) \cdot 1 \cdot 1 - 4 \cdot (-2) \cdot 2 \\ & = 4 -6 -4 -6+1+16 \\[2ex] & = \bm{5} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-64078968233ec50d2e793309d55e55fc_l3.png)
التمرين 3
أوجد حل محدد المصفوفة 3×3 التالية:
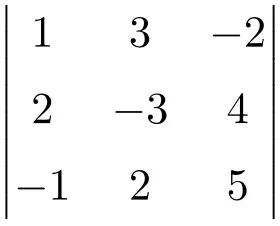
لتحديد مصفوفة 3×3، يجب علينا استخدام قاعدة ساروس:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix}1 & 3 & -2 \\[1.1ex] 2 & -3 & 4 \\[1.1ex] -1 & 2 & 5 \end{vmatrix} & = \\ & = 1 \cdot (-3) \cdot 5 + 3 \cdot 4 \cdot (-1) + 2 \cdot 2 \cdot (-2) \ - \\[1.1ex] & \phantom{=} - (-1) \cdot (-3) \cdot (-2) - 2 \cdot 4 \cdot 1 - 2 \cdot 3 \cdot 5 \\[2.5ex] & = -15 -12 -8 +6-8-30 \\[2.5ex] & = \bm{-67} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fd4494ae66a604834b8f9f47fcbbe41d_l3.png)
التمرين 4
أوجد حل محدد المصفوفة من الرتبة الثالثة التالية:
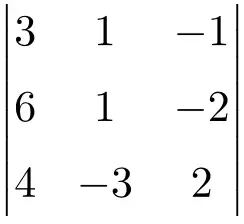
لإيجاد حل محدد مصفوفة 3×3 يجب علينا تطبيق صيغة ساروس:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 3 & 1 & -1 \\[1.1ex] 6 & 1 & -2 \\[1.1ex] 4 & -3 & 2 \end{vmatrix} & = \\ & = 3 \cdot 1 \cdot 2 + 1 \cdot (-2) \cdot 4 + 6 \cdot (-3) \cdot (-1) \ - \\[1.1ex] & \phantom{=} - 4 \cdot 1 \cdot (-1) - (-3) \cdot (-2) \cdot 3 - 6 \cdot 1 \cdot 2 \\[2.5ex] & =6 -8 +18 +4-18-12 \\[2.5ex] & = \bm{-10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e811024d460a60a1df59983b1f700e8_l3.png)
التمرين 5
أوجد قيمة
![]()
والذي يلغي المحدد الثالث التالي:
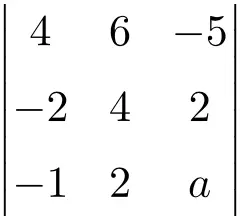
نحسب أولاً، باستخدام قاعدة ساروس، قيمة المحدد كدالة لـ
![]()
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned}\begin{vmatrix} 4 & 6 & -5 \\[1.1ex] -2 & 4 & 2 \\[1.1ex] -1 & 2 & a \end{vmatrix} & = \\ & = 4 \cdot 4 \cdot a + 6 \cdot 2 \cdot (-1) + (-2) \cdot 2 \cdot (-5) \ - \\[1.1ex] & \phantom{=}- (-1) \cdot 4 \cdot (-5) - 2 \cdot 2 \cdot 4 - (-2) \cdot 6 \cdot a \\[2.5ex] & = 16a -12 + 20 - 20 - 16 +12a \\[2.5ex] & = 28a -28 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-07e67cfc5e45c0a11c35d643cd4c1c78_l3.png)
لكي يختفي المحدد يجب أن تكون النتيجة 0. لذلك، نجعل النتيجة تساوي 0 ونحل المعادلة:
![]()
![]()
![]()