الوظيفة العقلانية: ما هي، المجال، الخطوط المقاربة، الرسم البياني، التمارين،...

هنا سوف تكتشف ما هي الوظائف العقلانية. بالإضافة إلى ذلك، سنشرح كيفية حساب المجال وخطوط التقارب للدالة الكسرية. وليس هذا فحسب، بل سترى ما هي جميع خصائص الوظائف العقلانية. وأخيرًا، يمكنك التدرب من خلال تمارين خطوة بخطوة على الوظائف العقلانية.

ما هي وظيفة عقلانية؟

تعريف الدالة العقلانية هو كما يلي:

الدالة الكسرية هي دالة مكونة من حاصل قسمة كثيرتي الحدود ، أي أن الدالة الكسرية عبارة عن كسر يحتوي على كثيرة حدود في البسط والمقام.

تتميز الوظائف العقلانية بالتفردات عند النقاط التي يختفي فيها المقام.

$f(x)=\cfrac{a_0+a_1x+a_2x^2+\dots +a_nx^n}{b_0+b_1x+b_2x^2+\dots +n_nx^n}$

تسمى الوظائف العقلانية أيضًا بالوظائف الكسرية.

ومن ناحية أخرى، لا ينبغي الخلط بين الوظائف العقلانية والوظائف غير العقلانية. الوظائف غير العقلانية (أو الجذرية) هي تلك التي تتكون من جذور.

أمثلة على الوظائف العقلانية

لفهم فكرة الوظيفة العقلانية بشكل أفضل، سنرى عدة أمثلة على هذا النوع من الوظائف.

دالة عقلانية مع متعددة الحدود من الدرجة الأولى في البسط والمقام:

$f(x)=\cfrac{x+3}{2x-5}$

تسمى هذه الأنواع من الوظائف العقلانية أيضًا وظائف التماثل .

دالة كسرية بها ثابت في البسط ومتعددة الحدود في المقام:

$f(x)=\cfrac{7}{x+1}$

تسمى هذه الأنواع من الوظائف العقلانية وظائف التناسب العكسي وتستخدم لتحديد الكميات المتناسبة عكسيا رياضيا.

دالة كسرية ذات متعددة حدود من الدرجة الثالثة في البسط ومتعددة حدود من الدرجة الثانية في المقام:

$f(x)=\cfrac{x^3+4x^2-2x+6}{x^2+3x-1}$

مجال الوظيفة العقلانية

الرقم المقسوم على 0 هو عدم تحديد يعطي ما لا نهاية (∞)، لذا فإن الدالة المنطقية ستكون موجودة دائمًا ما لم يكن المقام هو 0.

ولذلك فإن مجال الدالة الكسرية يتكون من جميع الأعداد الحقيقية ما عدا القيم التي تلغي المقام.

لذا، للحصول على مجال الدالة الكسرية، علينا معرفة متى يكون المقام 0، لأن هذه النقطة ستكون الوحيدة التي لا تنتمي إلى المجال

دعونا نرى كيف يتم حساب مجال الدالة الكسرية من خلال حل مثال:

$f(x)=\cfrac{5x}{x+2}$

نجعل المقام أولًا يساوي 0، ثم نحل المعادلة الناتجة:

$x+2=0$

$x=-2$

لذلك، عندما تكون x هي -2، سيكون المقام 0 وبالتالي لن تكون الدالة موجودة. وبالتالي فإن مجال الدالة يتكون من جميع الأعداد الحقيقية باستثناء x=-2. وبيان ذلك على النحو التالي:

$\text{Dom } f= \mathbb{R}-\{ -2 \}$

الخطوط المقاربة للدالة العقلانية

إحدى الخصائص الرئيسية للدوال العقلانية هي الخطوط المقاربة، لأنها تحدد تمثيلها الرسومي.

➤ انظر: التمثيل الرسومي للدالة

الخطوط المقاربة للدالة العقلانية هي الخطوط التي يقترب منها الرسم البياني للدالة إلى أجل غير مسمى ولكن لا يلمسها أبدًا.

هناك ثلاثة أنواع من الخطوط المقاربة: الخطوط المقاربة الرأسية، الخطوط المقاربة الأفقية، والخطوط المقاربة المائلة.

يوجد أدناه الأنواع الثلاثة من الخطوط المقاربة التي يمكن للدالة المنطقية رسمها بيانيًا باللون الأحمر.

الخط المقارب العمودي للدالة العقلانية

الخط المقارب الأفقي للدالة العقلانية

الخط المقارب للدالة العقلانية

كما ترون، تحديد الخط المقارب للدالة من الرسم البياني الخاص بها هو أمر بسيط للغاية، ولكن حساب الخطوط المقاربة للدالة العقلانية دون تمثيل الرسم البياني الخاص بها هو أمر معقد للغاية. ولهذا السبب نوصي بمعرفة كيفية حساب الخطوط المقاربة للدالة على موقعنا.

خصائص الوظيفة العقلانية

الوظائف العقلانية لها الخصائص التالية:

$f(x)=\cfrac{P(x)}{Q(x)}$

كما رأينا أعلاه، فإن مجال الدوال الكسرية يشمل جميع الأعداد الحقيقية باستثناء القيم التي تلغي مقام الكسر.

بشكل عام، يشمل نطاق (أو مدى) الدالة الكسرية جميع الأعداد الحقيقية باستثناء القيم التي تحتوي فيها الدالة على خط تقارب أفقي.

الوظائف العقلانية مستمرة في جميع أنحاء مجالها. أو بعبارة أخرى، تظهر الدوال العقلانية انقطاعات في نقاط لا تنتمي إلى مجالها.

يتكون التمثيل الرسومي لمعظم الوظائف العقلانية من قطعتين زائدتين.

يمكن استخلاص بعض القواعد الخاصة بالخطوط المقاربة للدوال العقلانيّة من البسط كثير الحدود.
$P(x)$

والمقام كثير الحدود

$Q(x):$
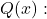
- تحتوي الدالة العقلانية على خط تقارب رأسي عند النقاط التي تمثل جذور
  $Q(x)$
  
  ولكن هذه ليست جذور
  
  $P(x).$
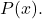
- إذا كانت درجة
  $P(x)$
  
  أقل من درجة
  
  $Q(x)$
  
  ، السطر y=0 هو خط مقارب أفقي للدالة العقلانية.
- إذا كانت درجة
  $P(x)$
  
  أكبر من درجة
  
  $Q(x)$
  
  ، الدالة العقلانية ليس لها خط تقارب أفقي.
- إذا كانت درجة
  $P(x)$
  
  هي وحدة أكبر من درجة
  
  $Q(x)$
  
  وليس لدى كثيرتي الحدود جذر مشترك، فالدالة العقلانية لها خط مقارب مائل.

تمارين محلولة على الوظائف العقلانية

التمرين 1

أوجد مجال الدالة الكسرية التالية:

$f(x)=\displaystyle\frac{4x}{2x+4}$

انظر الحل

إنها دالة كسرية، لذا فإن المجال يتكون من جميع الأرقام باستثناء تلك التي تلغي المقام، لأن الدالة عندها ستعطي ∞.

لذلك قمنا بتعيين المقام الصحيح يساوي الصفر لمعرفة الرقم الذي لا ينتمي إلى المجال:

$2x+4=0$

ونحل المعادلة الناتجة:

$2x=-4$

$x=\cfrac{-4}{2}=-2$

وبالتالي فإن مجال الدالة يتكون فقط من أرقام باستثناء -2:

$\mathbf{Dom } \ \bm{f = \mathbb{R}- \{ -2 \} }$

تمرين 2

أوجد نقاط القطع للدالة المنطقية التالية باستخدام المحاور الديكارتية:

$f(x)=\cfrac{x^2-9}{x}$

انظر الحل

نقطة القطع مع المحور X

للعثور على نقطة تقاطع الدالة مع المحور X من الضروري حلها

$f(x)=0:$

$f(x)=0$

$\cfrac{x^2-9}{x}=0$

$x^2-9=0\cdot x$

$x^2-9=0$

$x^2=9$

$x^2=\pm 3$

حصلنا على حلين للمعادلة التربيعية، بحيث تتقاطع الدالة الكسرية مع محور الإحداثي المحوري عند نقطتين مختلفتين وهما:

$\bm{(3,0)\qquad (-3,0)}$

نقطة القطع مع المحور Y

للعثور على نقطة التقاطع مع المحور Y يجب عليك حساب

$f(0):$

$f(0)=\cfrac{0^2-9}{0}=\cfrac{-9}{0}= \infty$

أي عدد مقسوم على صفر هو عدم تعيين ويعطي ما لا نهاية. ولذلك، فإن الدالة الكسرية لا تمر بأي نقطة فوق المحور Y، أي أنه ليس لها نقطة تقاطع مع المحور Y.

التمرين 3

ارسم الدالة المنطقية التالية على الرسم البياني:

$y=\cfrac{2x+3}{2x+6}$

انظر الحل

أول شيء يجب فعله هو حساب مجال الدالة:

$2x+6=0$

$2x =-6$

$x =\cfrac{-6}{2} =-3$

$\text{Dom } f = \mathbb{R} - \{ -3 \}$

بمجرد أن نعرف مجال الدالة، نقوم بإنشاء جدول القيم:

$\begin{array}{c|c} x & y \\ \hline -2,5 & -2 \\ -2 & -0,5 \\ -1 & 0,25 \\ 1 & 0,63 \\ -3,5 & 4 \\ -4 & 2,5 \\ -5 & 1,75 \\ -7 & 1,38\end{array}$

للإنهاء، ما عليك سوى تمثيل النقاط التي تم الحصول عليها على الرسم البياني ورسم القطع الزائدة، وبالتالي رسم الدالة الكسرية:

التمرين 4

حدد الخطوط المقاربة للدالة العقلانية الموضحة أدناه:

انظر الحل

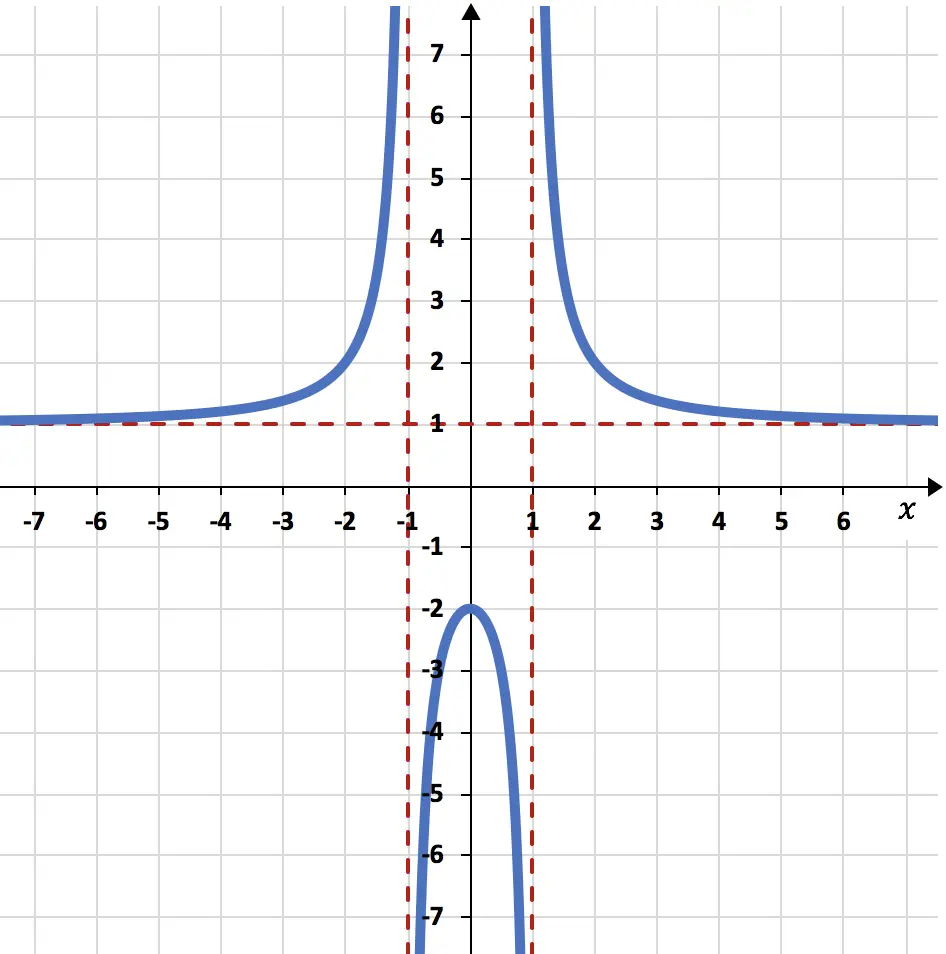
الخطوط المقاربة واضحة جدًا على الرسم البياني، حيث يتم تمثيلها كخطوط منقطة حمراء.

في هذه المشكلة، تكون الدالة قريبة جدًا من الخط الأفقي y=1 ولكنها لا تلمسه أبدًا. ولذلك، فإن الدالة العقلانية لها خط تقارب أفقي واحد، وهو y=1.

وبالمثل، فإن التمثيل الرسومي للدالة قريب جدًا من الخطوط الرأسية x=-1 وx=1، لكنه لا يصل أبدًا إلى هذه القيم. وبالتالي، فإن الدالة العقلانية لها خطان مقاربان رأسيان مختلفان، وهما x=-1 وx=1.

التمرين 5

احسب جميع الخطوط المقاربة للدالة العقلانية التالية:

$\displaystyle f(x)=\frac{6x-4}{2x+2}$

ملحوظة: لحل هذا التمرين، نوصيك أولاً بالانتقال إلى الرابط أعلاه للتعرف على كيفية حساب الخطوط المقاربة للدالة والاطلاع على الشرح.

انظر الحل

الخط المقارب الرأسي

لحساب الخطوط المقاربة الرأسية للدالة، علينا أولًا إيجاد مجال الدالة. ولذلك، فإننا نجعل مقام الدالة الكسرية يساوي 0 للعثور على النقاط التي لا تنتمي إلى المجال:

$2x +2 =0$

$2x= -2$

$x = \cfrac{-2}{2} = -1$

وبالتالي فإن مجال الدالة يتكون من جميع الأرقام باستثناء -1:

$\text{Dom } f = \mathbb{R} - \left\{ -1 \right\}$

إذن x=-1 يمكن أن يكون خطًا مقاربًا رأسيًا. للتحقق من ذلك، يجب علينا حساب نهاية الدالة عند النقطة:

$\displaystyle \lim_{x \to -1 } \frac{6x-4}{2x+2} = \frac{6\cdot(-1)-4}{2\cdot(-1)+2}=\frac{-10}{0}= \infty$

لذلك، x=-1 هو خط مقارب رأسي للدالة العقلانية، لأن نهاية الدالة عند هذه النقطة تعطي ما لا نهاية.

الخط المقارب الأفقي

لتحديد الخطوط المقاربة الأفقية، نحتاج إلى حساب الحد اللانهائي للدالة:

$\displaystyle \lim_{x \to +\infty}\frac{6x-4}{2x+2} = \frac{6(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{6}{2} = \bm{3}$

$\displaystyle \lim_{x \to -\infty}\frac{6x-4}{2x+2} = \frac{6(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{6}{2} = \bm{3}$

في هذه الحالة، نتيجة الحد اللانهائي غير المحدد بين اللانهاية هو تقسيم معاملات x من أعلى درجة، حيث أن البسط والمقام من نفس الترتيب.

الحدان اللانهائيان للدالة أعطانا 3، لذا فإن y=3 هو خط تقارب أفقي للدالة المنطقية.

الخط المقارب

نظرًا لوجود خط تقارب أفقي، فإن الدالة العقلانية لا تحتوي على خط تقارب مائل.

ما هي وظيفة عقلانية؟

أمثلة على الوظائف العقلانية

مجال الوظيفة العقلانية

الخطوط المقاربة للدالة العقلانية

خصائص الوظيفة العقلانية

تمارين محلولة على الوظائف العقلانية

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

اترك تعليقاً إلغاء الرد