▷ كيفية معرفة ما إذا كانت الدالة متصلة (تمارين محلولة)

نوضح في هذه المقالة ما هي الدوال المستمرة وكيفية تحديد ما إذا كانت الدالة مستمرة عند نقطة ما أم لا. بالإضافة إلى ذلك، سوف تجد خصائص الوظائف المستمرة وتحليل الاستمرارية للوظائف الأكثر شيوعا. وأخيرًا، يمكنك التدرب على التمارين المحلولة على الدالة المستمرة لفهم المفهوم بشكل كامل.

ما هي الدالة المستمرة؟

يمكن دراسة استمرارية الوظيفة بيانيا. الدالة المستمرة هي دالة يمكن تمثيلها على الرسم البياني دون إزالة قلم الرصاص من الورقة.

وظيفة مستمرة

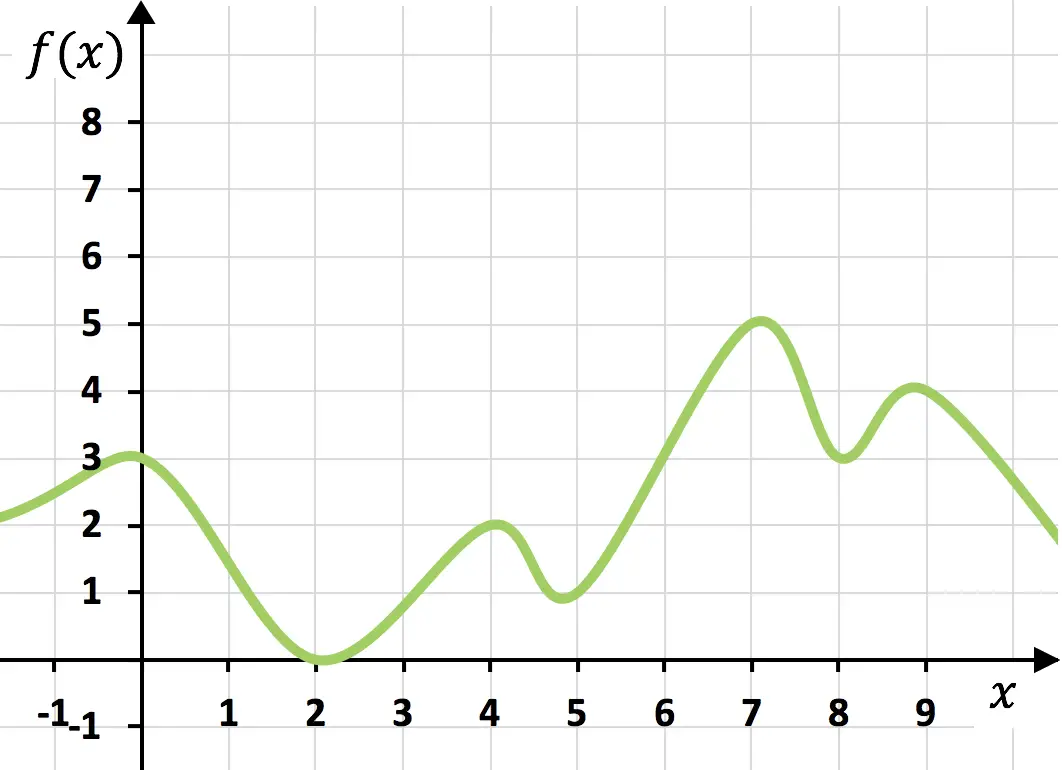
الوظيفة المذكورة أعلاه مستمرة لأنه يمكن رسمها بضربة واحدة دون رفع يدك عن الورقة.

ومن ناحية أخرى، عندما لا يتم وضع شرط الاستمرارية السابق في دالة، يقال إنها دالة متقطعة .

وظيفة متقطعة

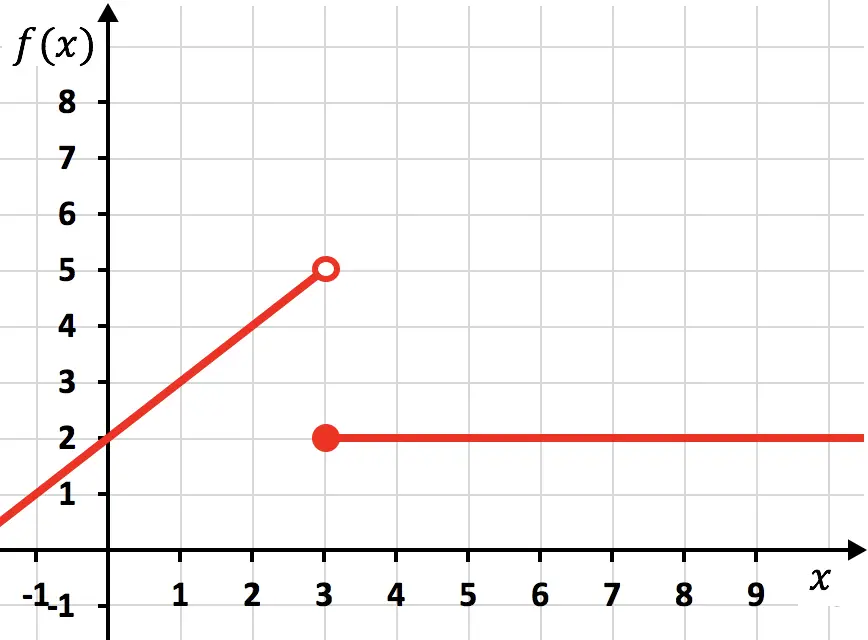
الوظيفة السابقة متقطعة لأنه لتمثيلها عليك رسم خطين بالقلم الرصاص. في هذه الحالة، تتوقف الدالة عن أن تكون متصلة عند x=3، لذلك نقول أن x=3 هي نقطة انقطاع .

بالإضافة إلى ذلك، هناك ثلاثة أنواع من الانقطاعات : الانقطاع الذي يمكن تجنبه، وانقطاع القفزة المحدودة الحتمية، وانقطاع القفزة اللانهائية الحتمية. وفي الرابط التالي يمكنك أن ترى كيف يبدو كل نوع من أنواع عدم الاستمرارية وما هو المختلف في كل منها:

➤ انظر: أنواع الانقطاعات

استمرارية الدالة عند نقطة ما

بمجرد أن نرى كيف يبدو الرسم البياني للدالة المستمرة، سننظر في كيفية معرفة ما إذا كانت الوظيفة مستمرة أم لا من الناحية التحليلية.

رياضياً، تكون الدالة متصلة عند نقطة ما إذا تم استيفاء الشروط الثلاثة التالية:

الدالة موجودة عند هذه النقطة، أي أن صورة النقطة موجودة.

$\exists \ f(a)$

هناك حد للوظيفة في هذه المرحلة. ومن ثم، فإن الحدين الجانبيين الأيسر والأيمن للدالة عند هذه النقطة متساويان.

$\displaystyle \lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) \quad \color{orange}\bm{\longrightarrow}\color{black} \quad \exists \lim_{x \to a} f(x)$

تتطابق صورة النقطة مع حد الدالة عند هذه النقطة.

$\displaystyle f(a)=\lim_{x \to a} f(x)$

وبالتالي، إذا تحققت شروط الاستمرارية الثلاثة في جميع نقاط الدالة، تكون الدالة متصلة.

على سبيل المثال، سوف نقوم بتحليل استمرارية الوظيفة المتعددة التعريف التالية:

حتى لو قمت بتغيير الأقسام، عند هذه النقطة

$x=-2$

الدالة متصلة، لأن الحدود الجانبية للدالة عند هذه النقطة متساوية وأكثر تطابقًا مع قيمة الدالة عند هذه النقطة.

$\lim\limits_{x \to -2^-} f(x)=\lim\limits_{x \to -2^+} f(x)= f(-2)=3$

ومن ناحية أخرى، فإن الدالة ليست مستمرة عند هذه النقطة

$x=4$

لأن النهايتين الجانبيتين مختلفتان، وبالتالي فإن نهاية الدالة غير موجودة عند هذه النقطة:

$\lim\limits_{x \to 4^-} f(x)=3 \neq \lim\limits_{x \to 4^+} f(x)= 2$

باختصار، الدالة المحددة بالقطع تكون متصلة في جميع الأعداد الحقيقية ما عدا في

$x=4,$

حيث يوجد انقطاع.

يمكننا أيضًا التحقق من أن الوظيفة متقطعة

$x=4$

لأنه لتمثيلها بيانياً من الضروري إزالة قلم الرصاص من الورقة في هذه المرحلة.

استمرارية الوظائف الأولية

أنواع معينة من الوظائف مستمرة حسب خصائصها:

الدوال الثابتة مستمرة في جميع الأعداد الحقيقية.

$f(x)=k$

دوال كثيرة الحدود مستمرة لجميع الأعداد الحقيقية.

$f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n$

تكون الدوال المنطقية (أو الكسرية) متصلة في جميع الأعداد الحقيقية باستثناء القيم التي تلغي مقام الكسر، وعند هذه النقاط تمثل الدالة انقطاعًا.

$f(x)=\cfrac{p(x)}{q(x)}$

الدوال الأسية متصلة على جميع الأعداد الحقيقية:

$f(x)=a^x$

الدوال اللوغاريتمية متصلة في جميع النقاط التي تجعل حجتها موجبة.

$f(x)=\log_a (x)$

استمرارية الدوال غير المنطقية ، أو الدوال ذات الجذور، تعتمد على مؤشر الجذر (n). إذا كان الفهرس زوجيًا، فهذه دوال متصلة في جميع النقاط تجعل الوسيطة الجذرية تساوي أو أكبر من الصفر. لكن إذا كان المؤشر فرديًا، فهو دوال متصلة على جميع الأعداد الحقيقية.

$f(x)=\sqrt[n]{x}$

تعتمد استمرارية الدوال المثلثية على نوع الدالة. دالة الجيب وجيب التمام مستمرتان على مجموعة الأعداد الحقيقية، لكن دالة الظل غير متصلة عند النقاط
$\displaystyle x=\frac{\pi}{2}+k\pi$

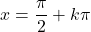
(حيث k عدد صحيح).

$f(x)=sen(x)\qquad f(x)=cos(x)\qquad f(x)=tg(x)$

خصائص الدوال المستمرة

شون

$f(x)$

$g(x)$

وظيفتين مستمرتين عند هذه النقطة

$x=a,$

مجموع وظيفتين متصلتين عند نقطة ما هو دالة متصلة أخرى عند تلك النقطة.

$f(x)+g(x)$

حاصل ضرب دالتين متصلتين عند نقطة ما يساوي دالة متصلة أخرى عند تلك النقطة.

$f(x)\cdot g(x)$

قسمة دالتين متصلتين عند نقطة ما ينتج عنه دالة متصلة أخرى عند تلك النقطة، ما دامت تلك النقطة لا تلغي دالة القسمة.

$\cfrac{f(x)}{g(x)}\qquad g(a)\neq 0$

إن تكوين وظيفتين متصلتين عند نقطة ما يؤدي إلى ظهور دالة مستمرة عند نفس النقطة.

$f(x)\circ g(x)$

➤ انظر: ما هي الوظيفة المركبة؟

حل تمارين على استمرارية الدالة

التمرين 1

أوجد انقطاعات الدالة الموضحة في الرسم البياني التالي. حدد أيضًا نوع الانقطاع.

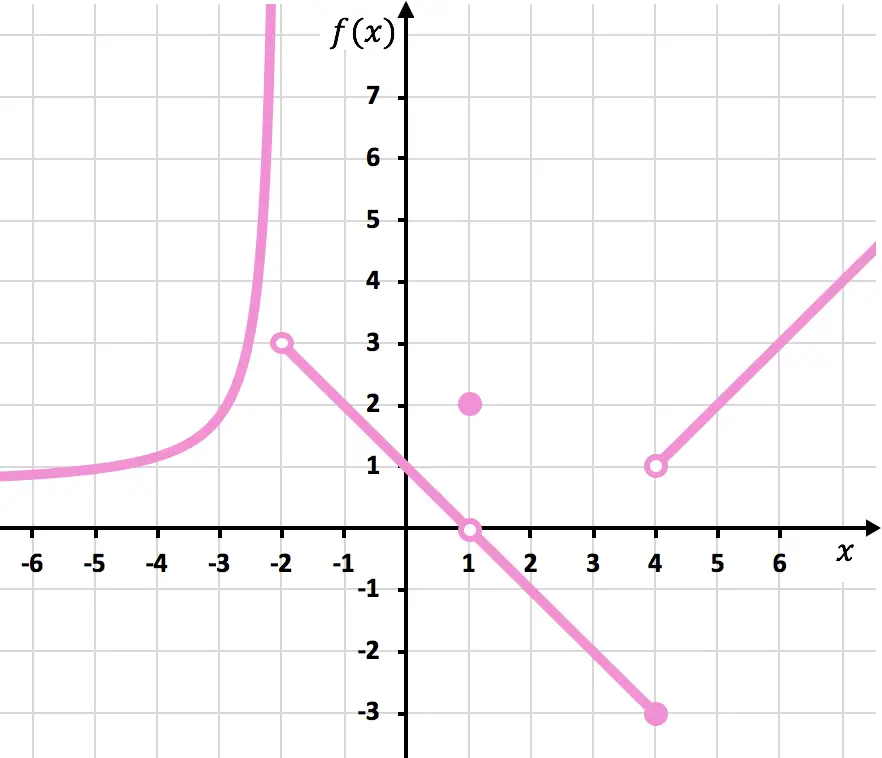
ملاحظة: لتنفيذ هذا التمرين، نوصيك أولاً بمعرفة الأنواع المختلفة للانقطاعات وكيفية تحديدها. يمكنك رؤية الشرح في مبدأ رابط أنواع الانقطاع .

انظر الحل

لرسم الدالة يجب عليك رفع قلم الرصاص عند x=-2، عند x=1 وعند x=4. وبالتالي فإن الوظيفة متقطعة عند هذه النقاط الثلاث.

عند x=-2، حد الجانب الأيسر هو +∞ وحد الجانب الأيمن هو 3. وبالتالي، نظرًا لأن أحد الحدود الجانبية لا نهائي، فإن الدالة لها انقطاع قفز لا نهائي لا مفر منه عند x=-2.

$\displaystyle \lim_{x \to -2^-} f(x) = +\infty \ \neq \ \lim_{x \to -2^+} f(x) = 3$

حد الدالة عند x=1 هو 0، ومن ناحية أخرى، قيمة الدالة عند x=1 تساوي 2. وبالتالي فإن الدالة تمثل انقطاعًا يمكن تجنبه عند x=1.

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 0 \ \bm{\longrightarrow} \ \lim_{x \to 1} f(x) = 0$

$\displaystyle \lim_{x \to 1} f(x) = 0 \neq f(0) = 2$

عند x = 4، حد الجانب الأيسر هو -3 وحد الجانب الأيمن هو 1. لذلك، نظرًا لأن الحدين الجانبيين مختلفان ولا يعطي أي منهما ما لا نهاية، فإن الدالة لها حتماً انقطاع قفز محدود عند x =4.

$\displaystyle \lim_{x \to 4^-} f(x) = -3 \ \neq \ \lim_{x \to 4^+} f(x) = 1$

تمرين 2

حدد النقاط التي تكون فيها الدالة الموضحة في الرسم البياني التالي غير متصلة.

انظر الحل

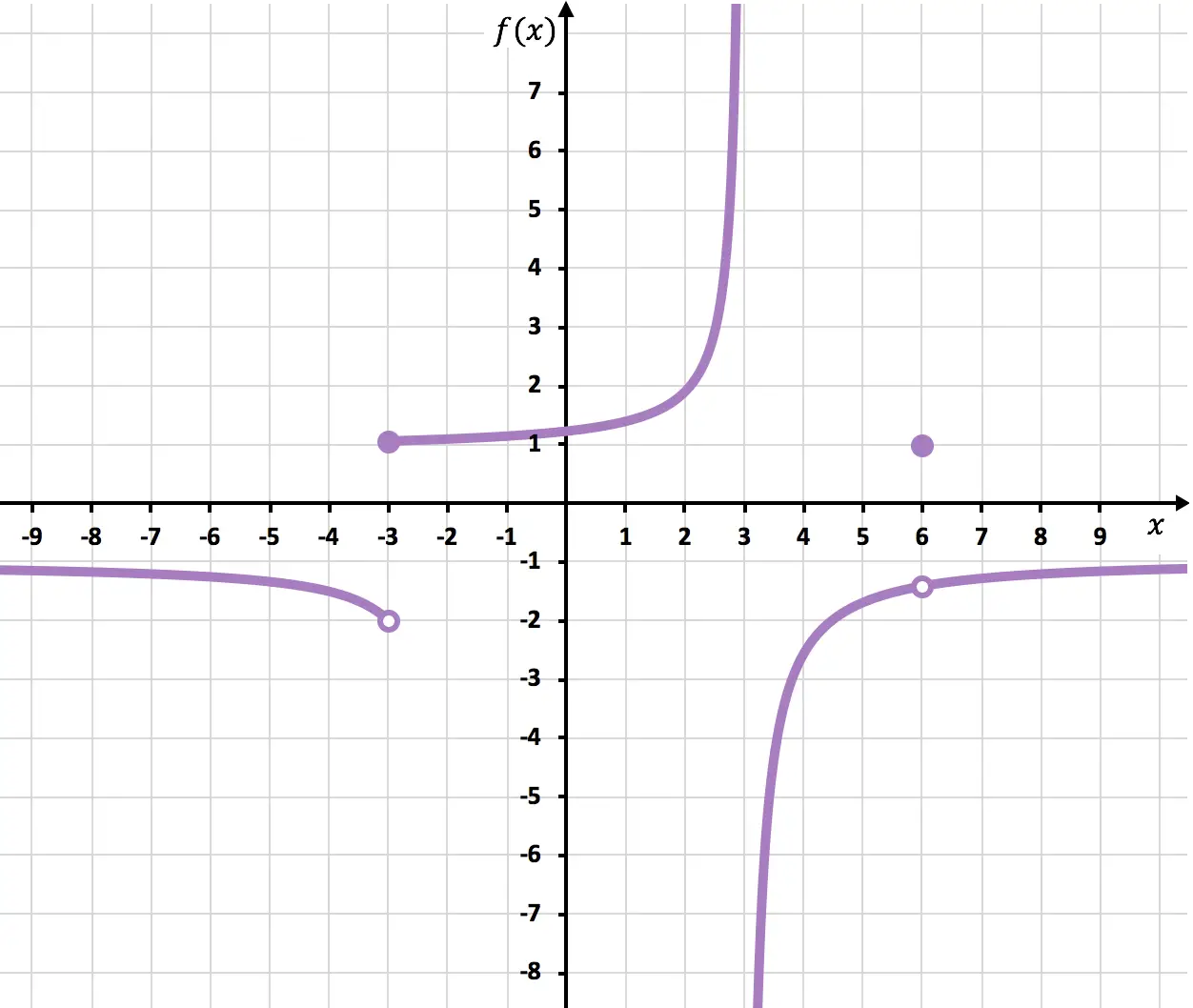
عند النقطة x=6 تنقطع الوظيفة بسبب وجود نقطة مفتوحة. الحد عندما تقترب x من 6 هو -1.4 لكن f(6)=1. وبالتالي فإن الدالة لها انقطاع يمكن تجنبه عند x=6 لأن قيمة الحد لا تتطابق مع قيمة الدالة:

$\displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4$

$\displaystyle\lim_{x \to 6} f(x)=-1,4 \neq f(6)=1$

عند x=-3 لا تتطابق الحدود الجانبية ولا شيء يعطي اللانهاية. وبالتالي فإن الدالة لها انقطاع قفزة محدود لا مفر منه عند x=-3.

$\displaystyle \lim_{x \to -3^-} f(x)=-2 \neq \lim_{x \to -3^+} f(x)=1$

وأخيرًا، الدالة لها انقطاع لا نهائي لا مفر منه عند x = 3، نظرًا لأن حدًا جانبيًا واحدًا على الأقل عند هذه النقطة يؤدي إلى ما لا نهاية.

$\displaystyle \lim_{x \to 3^-} f(x)=+\infty \qquad \lim_{x \to 3^+} f(x)=-\infty$

التمرين 3

تحليل استمرارية الوظيفة العقلانية التالية:

$\displaystyle f(x)= \frac{2}{x-5}$

انظر الحل

الدوال الكسرية متصلة في مجالها بأكمله، أي في جميع الأعداد الحقيقية باستثناء القيم التي تلغي المقام. لذلك، قمنا بمساواة مقام الدالة الكسرية بالصفر لمعرفة النقاط التي لا تنتمي إلى المجال:

$x-5=0$

$x=5$

$\text{Dom } f = \mathbb{R} - \{5\}$

وبالتالي ستكون الدالة متصلة في جميع النقاط باستثناء x=5.

التمرين 4

تحليل استمرارية الوظيفة المتعددة التعريف التالية:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 5x-2 & \text{si} & x < 1 \\[2ex] x^2+2 & \text{si} & x \geq 1 \end{array} \right.$

انظر الحل

الدالة مستمرة كذلك في القسم الأول،

$5x-2$

كما في القسم الثاني

$x^2+2$

، لأنها وظائف متعددة الحدود.

إذن النقطة الوحيدة التي يمكن أن تكون الدالة عندها غير متصلة هي النقطة التي تنقطع فيها الدالة جزئيًا. لذلك دعونا نحسب الحدود الجانبية عند هذه النقطة:

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1} (5x-2)=5\cdot 1-2=\bm{3}$

$\displaystyle \lim_{x \to 1^+} f(x) = \lim_{x \to 1} (x^2+2)=1^2+2=\bm{3}$

وبالتالي فإن الحدين الجانبيين يتطابقان، فإن نهاية الدالة عندما تميل x إلى 1 تساوي 3:

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 3 \ \bm{\longrightarrow} \ \exists \lim_{x \to 1} f(x) = 3$

علاوة على ذلك، فإن صورة x=1 هي أيضًا 3:

$f(1)=1^2+2=\bm{3}$

وبالتالي، بما أن نهاية الدالة عند x=1 تساوي صورة النقطة المذكورة، فإن الدالة متصلة عند النقطة x=1. ومن ثم فهي متصلة في جميع الأعداد الحقيقية.

$\displaystyle f(1)=\lim_{x \to 1} f(x)$

التمرين 5

ادرس استمرارية الدالة غير المنطقية التالية:

$f(x)=\sqrt{2x+6}$

انظر الحل

إنها دالة جذرية ذات فهرس زوجي، لذا ستكون الدالة مستمرة طالما أن وسيطة الجذر أكبر من 0 (لأن الجذر التربيعي لعدد سالب غير موجود):

$2x+6\ge 0$

نحن نحل عدم المساواة:

$2x\ge -6$

$x\ge \cfrac{-6}{2}$

$x\ge -3$

يتكون الحل من جميع الأعداد الأكبر من أو تساوي -3. وبالتالي تكون الدالة متصلة على فترة مجالها:

$\mathbf{Dom } \ \bm{f = [-3,+\infty) }$

التمرين 6

تحليل استمرارية الدالة اللوغاريتمية التالية:

$f(x)=\log_3 (-3x+6)$

انظر الحل

هذه دالة لوغاريتمية، وليس هناك لوغاريتم رقم سالب ولا لوغاريتم 0. لذلك، ستكون الدالة موجودة طالما أن وسيطة اللوغاريتم موجبة (أكبر من الصفر):

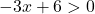$-3x+6>0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”95″ style=”vertical-align: -2px;”> <p class=$ نحن نحل عدم المساواة:

$-3x>-6″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”78″ style=”vertical-align: -2px;”> <p style=$

$x<\cfrac{-6}{-3}$

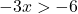
تذكر أنه عند قسمة عدد سالب على الطرف الآخر من المتراجحة، يجب عليك عكس إشارة المتراجحة.

$x<2$

يتكون الحل من جميع الأرقام الأقل من 2. وبالتالي فإن مجال تعريف الدالة هو:

$\mathbf{Dom } \ \bm{f = (-\infty,2) }$

وبالتالي فإن الدالة مستمرة عند كل نقطة في مجالها.

التمرين 7

احسب استمرارية الدالة التالية:

$f(x)=\cfrac{4x-2}{\sqrt{-2x-8}}$

انظر الحل

في مقام الكسر لدينا جذر ذو فهرس زوجي، وبالتالي فإن الدالة ستكون موجودة عندما تكون محتويات الجذر تساوي أو أكبر من الصفر:

$-2x-8\geq 0$

ولكن أيضًا، الجذر موجود في مقام الكسر، ولا يمكن أن يكون مقام الكسر 0 أبدًا. لذلك لن تكون الدالة موجودة إلا إذا كان محتوى الجذر أكبر من 0 تمامًا:

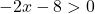$-2x-8> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”95″ style=”vertical-align: -2px;”> <p class=$ الآن نحل عدم المساواة:

$-2x>8″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”64″ style=”vertical-align: -2px;”> <p style=$

$x<\cfrac{8}{-2}$

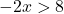
تذكر أنه عندما نغير أضلاع عدد سالب عن طريق ضرب المتباينة أو قسمتها، يجب علينا أيضًا تدوير علامة المتباينة.

$x<-4$

والنتيجة هي جميع الأرقام أقل من -4. وبالتالي يتم تحديد مجال الدالة، وبالتالي استمراريتها، من خلال الفترة التالية:

$\mathbf{Dom } \ \bm{f = (-\infty,-4) }$

التمرين 8

احسب قيمة k بحيث تكون الدالة مستمرة طوال الوقت

$\mathbb{R} .$

$\displaystyle f(x)= \left\{ \begin{array}{lcl} kx-1 & \text{si} & x \leq 2 \\[2ex] 3x^2 - 5 & \text{si} & x > 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”225″ style=”vertical-align: 0px;”> <div class=$

انظر الحل

لكي تكون الدالة متصلة، يجب أن يعطي الحدان الجانبيان عند نقطة الانفصال نفس النتيجة. لذلك نحسب أولاً الحد الجانبي عند نقطة الانكسار للجزء الذي لا يحتوي على k :

$\displaystyle \lim_{x \to 2^+} f(x) = \lim_{x \to 2} (3x^2 - 5) = 3\cdot 2^2-5=\bm{7}$

لذلك، لكي تكون الدالة متعددة التعريف متصلة، يجب أن تكون نهاية الجانب الآخر أيضًا مساوية لـ 7.

$\displaystyle \lim_{x \to 2^-} f(x) = \lim_{x \to 2} (kx-1) = k\cdot2 -1= 2k-1$

وبالتالي، لكي تكون الدالة متصلة، يجب أن يعطي الحدان الجانبيان لأي نقطة نفس النتيجة. ولذلك فإننا نجعل التعبير الذي تم الحصول عليه من النهاية يساوي 7 (نتيجة الحد الجانبي الآخر).