المعادلات الخطية -

ستجد هنا الصيغ لجميع أنواع معادلات الخط. بالإضافة إلى ذلك، ستتمكن من رؤية أمثلة لكيفية حسابها، بالإضافة إلى التدرب على حل التمارين لمعادلات الخط.

ما هي جميع معادلات الخط؟

تذكر أن التعريف الرياضي للخط هو مجموعة من النقاط المتتالية الممثلة في نفس الاتجاه بدون منحنيات أو زوايا.

وبالتالي، للتعبير تحليليًا عن أي خط مستقيم في المستوى (في R2) نستخدم معادلات الخط المستقيم، وللعثور عليها تحتاج فقط إلى نقطة تنتمي إلى الخط المستقيم ومتجه الاتجاه للخط المستقيم المذكور. باستخدام هذين العنصرين الهندسيين فقط، يمكنك العثور على جميع المعادلات المختلفة للخط، وهي كما يلي:

معادلات الخط هي المعادلة المتجهة، والمعادلات البارامترية، والمعادلة المستمرة، والمعادلة الضمنية (أو العامة)، والمعادلة الصريحة، ومعادلة نقطة الميل، والمعادلة الأساسية (أو القطاعية).

جميع أنواع المعادلات الخطية لها نفس الهدف: تمثيل الخط رياضيًا. لكن كل معادلة للخط لها خصائصها، وبالتالي، اعتمادًا على المشكلة، من الأفضل استخدام واحدة أو أخرى.

بعد أن رأينا مفهوم المعادلات الخطية، ننتقل الآن إلى تحليل خصائص كل نوع من المعادلات الخطية على وجه الخصوص. يوجد أدناه شرح تفصيلي للأنواع المختلفة من المعادلات في السطر، ولكن إذا أردت، يمكنك الانتقال مباشرة إلى نهاية الجدول الملخص مع صيغ جميع المعادلات الموجودة في السطر .

معادلة المتجهات للخط

نعم

$\vv{\text{v}}$

هو متجه الاتجاه للخط و

$P$

النقطة التي تنتمي إلى اليمين:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)$

صيغة المعادلة المتجهية للخط هي:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2) \end{empheq}$

ذهب:

$x$

و

$y$

هي الإحداثيات الديكارتية لأي نقطة على الخط.
$P_1$

و

$P_2$

هي إحداثيات نقطة معروفة تشكل جزءًا من الخط

$P(P}_1,P_2).$
$\text{v}_1$

و

$\text{v}_2$

هي مكونات متجه الاتجاه للخط

$\vv{\text{v}}=(\text{v}_1,\text{v}_2).$
$t$

هو عددي (عدد حقيقي) تعتمد قيمته على كل نقطة على السطر.

إنها معادلة متجهة للخط في المستوى، أي عند العمل مع نقاط ومتجهات إحداثيتين (في R2). ومع ذلك، إذا كنا نجري حسابات في الفضاء (في R3)، فسيتعين علينا إضافة عنصر إضافي إلى معادلة الخط:

$(x,y,z)=(P_1,P_2,P_3)+t\cdot (\text{v}_1,\text{v}_2,\text{v}_3)$

المعادلات البارامترية للخط

يمكن الحصول على المعادلات البارامترية للخط من معادلته المتجهة:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

نقوم أولاً بضرب المعلمة

$t$

بواسطة متجه الاتجاه لليمين:

$(x,y)=(P_1,P_2)+ (t\cdot\text{v}_1,t\cdot\text{v}_2)$

بعد ذلك، نضيف إحداثيات X وY:

$(x,y)=(P_1+t\cdot\text{v}_1,P_2+t\cdot\text{v}_2)$

وأخيرًا، بعد مسح كل متغير على حدة، نحصل على المعادلات البارامترية للخط:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases} \end{empheq}$

ذهب:

$x$

و

$y$

هي الإحداثيات الديكارتية لأي نقطة على الخط.
$P_1$

و

$P_2$

هي إحداثيات نقطة معروفة تشكل جزءًا من الخط

$P(P}_1,P_2).$
$\text{v}_1$

و

$\text{v}_2$

هي مكونات متجه الاتجاه للخط

$\vv{\text{v}}=(\text{v}_1,\text{v}_2).$
$t$

هو عددي (عدد حقيقي) تعتمد قيمته على كل نقطة على السطر.

كما كان من قبل، هذه هي المعادلات البارامترية للخط في المستوى (في R2)، ولكن للعثور على المعادلات البارامترية للخط في الفضاء (في R3) سيكون من الضروري إضافة معادلة أخرى للمتغير الثالث Z:

$\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \\[1.7ex] z=P_3+t\cdot\text{v}_3\end{cases}$

المعادلة المستمرة للخط

يمكن استنتاج المعادلة المستمرة لأي خط من معادلاته البارامترية:

$\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

إذا قمنا بمسح الإعداد

$t$

من كل معادلة بارامترية نحصل على التعبيرات التالية:

$t =\cfrac{x-P_1}{\text{v}_1}}$

$t =\cfrac{y-P_2}{\text{v}_2}}$

هـ بمساواة المعادلتين الناتجتين نحصل على المعادلة المستمرة للخط:

$t= t$

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

باختصار، المعادلة المستمرة للخط هي:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2} \end{empheq}$

ذهب:

$x$

و

$y$

هي الإحداثيات الديكارتية لأي نقطة على الخط.
$P_1$

و

$P_2$

هي إحداثيات نقطة معروفة تشكل جزءًا من الخط

$P(P}_1,P_2).$
$\text{v}_1$

و

$\text{v}_2$

هي مكونات متجه الاتجاه للخط

$\vv{\text{v}}=(\text{v}_1,\text{v}_2).$

هذه الصيغة مخصصة للمعادلة المستمرة للخط عند العمل في بعدين (ثنائي الأبعاد). ولكن إذا كنا نجري عمليات في 3 أبعاد (3D)، فسنحتاج إلى إضافة عنصر إضافي إلى المعادلة الخطية:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}= \cfrac{z-P_3}{\text{v}_3}$

المعادلة الضمنية أو العامة للخط

نعم

$\vv{\text{v}}$

هو متجه الاتجاه للخط و

$P$

النقطة التي تنتمي إلى اليمين:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)$

صيغة المعادلة الضمنية أو العامة أو الديكارتية للخط هي:

ذهب:

$x$

و

$y$

هي الإحداثيات الديكارتية لأي نقطة على الخط.
المعامل
$A$

هو المكون الثاني لمتجه الاتجاه للخط:

$A=\text{v}_2}$
المعامل
$B$

هو المكون الأول لعلامة تغير اتجاه المتجه:

$B=-\text{v}_1}$
المعامل
$C$

يتم حسابه عن طريق استبدال النقطة المعروفة

$P$

في معادلة الخط.

الصيغة، يمكن أيضًا الحصول على المعادلة الضمنية للخط عن طريق ضرب كسور المعادلة المستمرة.

معادلة صريحة للخط

صيغة المعادلة الصريحة للخط هي:

ذهب:

$m$

هو ميل الخط.
$n$

تقاطعه y، أي الارتفاع الذي يتقاطع عنده مع المحور Y.

في القسم أدناه سترى كيفية تحديد المعلمات

$m$

$n$

للخط المستقيم ولكن، على وجه الخصوص، هناك طريقة أخرى للعثور على المعادلة الصريحة وهي استخدام المعادلة الضمنية؛ ولهذا يجب حل المجهول

$y$

من المعادلة الضمنية

معنى المعلمات م و ن

كما رأينا في تعريف المعادلة الصريحة للخط المعلمة

$m$

هو ميل الخط و

$n$

تقاطع y الخاص به. لكن ماذا يعني هذا؟ دعونا نرى ذلك من التمثيل الرسومي للخط:

مصطلح مستقل

$\bm{n}$

هي نقطة تقاطع الخط مع محور الكمبيوتر (محور OY). على سبيل المثال، في الرسم البياني أعلاه

$n$

يساوي 1 لأن الخط يتقاطع مع المحور y عند y=1.

ومن ناحية أخرى فإن مصطلح

$\bm{m}$

يشير إلى ميل الخط ، أي ميله. كما ترون في الرسم البياني،

$m$

يساوي 2 لأن الخط يرتفع بمقدار وحدتين رأسيتين مقابل وحدة أفقية واحدة.

من الواضح أنه إذا كان الميل موجبًا فإن الدالة تتزايد (تصعد)، ومن ناحية أخرى إذا كان الميل سالبًا فإن الدالة تتناقص (تتجه لأسفل).

احسب ميل الخط

بمجرد أن نعرف بالضبط ما هو ميل الخط، دعونا نرى كيف يتم حسابه. وبالتالي، هناك ثلاث طرق مختلفة لتحديد ميل الخط عدديًا:

نظرا لنقطتين مختلفتين على الخط
$P_1(x_1,y_1)$

و

$P_2(x_2,y_2),$

ميل الخط يساوي:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

نعم
$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

هو متجه اتجاه الخط، وميله هو:

$m = \cfrac{\text{v}_2}{\text{v}_1}$

نعم
$\alpha$

هي الزاوية التي يشكلها الخط مع محور الإحداثي السيني (المحور X)، وميل الخط يعادل ظل الزاوية المذكورة:

$m = \text{tg}(\alpha )$

معادلة نقطة الميل للخط

صيغة معادلة نقطة الميل للخط هي:

ذهب:

$m$

هو ميل الخط.
$P_1, P_2$

هي إحداثيات نقطة على الخط

$P(P_1,P_2).$

المعادلة الكنسي أو القطاعية للخط

على الرغم من أن هذا البديل لمعادلة الخط أقل شهرة، إلا أنه يمكن الحصول على المعادلة القانونية للخط من نقاط تقاطع الخط مع المحاور الديكارتية.

لتكن نقطتا التقاطع مع محوري المستقيم المعطى:

قطع مع المحور X:

$(a,0)$

قطع مع المحور Y:

$(0,b)$

صيغة المعادلة الأساسية للخط هي:

في الرياضيات، تسمى المعادلة الأساسية للخط أيضًا معادلة قطعية أو معادلة متماثلة.

ومن جهة أخرى المعاملات

$a$

$b$

ويمكن العثور عليها أيضًا من المعادلة العامة للخط باستخدام الصيغ التالية:

$Ax+By+C=0$

$a = -\cfrac{C}{A} \qquad \qquad b = -\cfrac{C}{B}$

جميع معادلات الخط (الصيغ)

وباختصار، إليك جدول يوضح صيغ جميع معادلات الخط:

مثال لحساب معادلات الخط

الآن بعد أن رأينا الشرح الكامل لمعادلة الخط، دعونا نرى كيف يتم حل مشكلة نموذجية لمعادلات الخط:

أوجد جميع معادلات الخط الذي تحدده النقطة
$P$

والمتجه

$\vv{\text{v}}.$

$P(3,-1) \qquad \qquad \vv{\text{v}}=(2,4)$

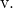
أولًا، نجد المعادلة المتجهية للخط من صيغته:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

ما عليك سوى استبدال إحداثيات النقطة والمتجه في الصيغة:

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(3,-1)+t\cdot (2,4)} \quad \vphantom{\Bigl(}}$

ثانياً: نجد المعادلات البارامترية للخط من خلال الصيغة المقابلة له:

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=3+2t} \\[1.7ex] \bm{y=-1+4t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

ونحدد أيضًا المعادلة المستمرة للخط بصيغته:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-3}{2}=\cfrac{y-(-1)}{4}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x-3}}{\bm{2}}\bm{=}\cfrac{\bm{y+1}}{\bm{4}}\quad \vphantom{\Biggl(}}$

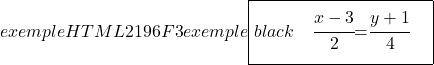
كما رأيت، من السهل حساب المعادلات المتجهة والبارامترية والمستمرة، ما عليك سوى استخدام الصيغ الخاصة بكل منها.

لننتقل الآن إلى إيجاد المعادلة العامة (أو الضمنية) للخط. للقيام بذلك، نعبر كسري المعادلة المستمرة:

$4\cdot (x-3)= 2 \cdot (y+1)$

$4x-12= 2y+2$

$4x-12-2y-2=0$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{4x-2y-14=0}\quad \vphantom{\Bigl(}}$

الآن يمكننا تحديد المعادلة الصريحة لحل الخط للمجهول

$y$

من المعادلة الضمنية:

$4x-2y-14=0$

$-2y=-4x+14$

$y=\cfrac{-4x+14}{-2}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=2x-7}\quad \vphantom{\Bigl(}}$

وبالتالي فإن ميل الخط يساوي 2 (الحد المرافق للمتغير المستقل

$x$

$m=2$

وبهذا يمكننا حساب معادلة نقطة الميل للخط بصيغته:

$y-P_2=m(x-P_1)$

$y-(-1)=2(x-3)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y+1=2(x-3)}\quad \vphantom{\Bigl(}}$

وأخيراً، لإيجاد المعادلة القطعية للخط نحسب نقاط تقاطعه مع المحورين OX وOY ثم نطبق صيغتها:

$y=2x-7$

نقطة التقاطع مع محور الإحداثي السيني (المحور X)

$y=0$

$0=2x-7$

$-2x=-7$

$x=\cfrac{-7}{-2} = \cfrac{7}{2}$

$\displaystyle \left(\frac{7}{2}, 0\right)$

نقطة التقاطع مع المحور y (المحور Y)

$x=0$

$y=2\cdot 0-7$

$y=-7$

$\displaystyle \left(0,-7\right)$

$\cfrac{x}{a}+\cfrac{y}{b} = 1$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\cfrac{\bm{x}}{\frac{\bm{7}}{\bm{2}}}+\cfrac{\bm{y}}{\bm{-7}} \bm{= 1} \quad \vphantom{\Biggl(}}$

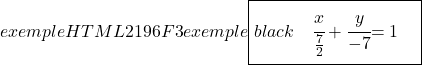
معادلة خط مستقيم يمر بنقطتين

هناك مشكلة أخرى شائعة جدًا في المعادلات الخطية وهي إيجاد معادلة الخط المحدد بنقطتين معلومتين. على الرغم من أنه يمكننا حساب متجه الاتجاه للخط ذي النقطتين ثم المعادلة، إلا أننا نقدم لك أدناه صيغة يمكنك من خلالها العثور على معادلة الخط المذكور بسهولة ويسر.

النظر في نقطتين تقع على الخط:

$P_1(x_1,y_1) \qquad \qquad P_2(x_2,y_2)$

صيغة العثور على معادلة الخط من نقطته هي:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} y-y_1= \cfrac{y_2-y_1}{x_2-x_1} (x-x_1) \end{empheq}$

تسمح لنا هذه الصيغة بحساب معادلة نقطة الميل للخط بشكل مباشر عندما يتم إعطاؤنا نقطتين يمر عبرهما الخط.

حل مسائل معادلات الخط

التمرين 1

أوجد المعادلة المتجهة والمعادلات البارامترية والمعادلة المستمرة للخط المحدد بالنقطة

$P$

وناقلها التوجيهي

$\vv{\text{v}}.$

كن كلا من:

$P(0,3) \qquad \qquad \vv{\text{v}}=(-1,5)$

انظر الحل

أولاً، نحسب المعادلة المتجهية للخط من صيغته:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(0,3)+t\cdot (-1,5)} \quad \vphantom{\Bigl(}}$

ثم نجد المعادلات البارامترية للخط باستخدام الصيغة المقابلة لها:

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\begin{cases} x=0+t\cdot (-1) \\[1.7ex] y=3+t\cdot 5\end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-t} \\[1.7ex] \bm{y=3+5t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

وأخيرًا، نحدد المعادلة المستمرة للخط بالصيغة الخاصة به:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-0}{-1}=\cfrac{y-3}{5}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x}}{\bm{-1}}\bm{=}\cfrac{\bm{y-3}}{\bm{5}}\quad \vphantom{\Biggl(}}$

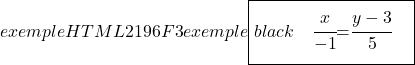
تمرين 2

أوجد المعادلة الضمنية والمعادلة الصريحة ومعادلة نقطة الميل للخط المحدد بالنقطة

$P$

ومتجه الاتجاه هو

$\vv{\text{v}}.$

$P(-4,3) \qquad \qquad \vv{\text{v}}=(2,6)$

انظر الحل

صيغة المعادلة الضمنية للخط هي:

$Ax+By+C=0$

لذلك يجب علينا إيجاد المعاملات A وB وC. ويتم الحصول على المجهولين A وB من إحداثيات متجه الاتجاه للخط، لأنه يتم التحقق دائمًا من المساواة التالية:

$\vv{\text{v}}= (-B,A)$

وبالتالي، فإن المعامل A هو الإحداثي الثاني للمتجه، والمعامل B هو الإحداثي الأول لعلامة المتجه المتغيرة:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}= (2,6) \end{array} \right\}\longrightarrow \begin{array}{l}A=6 \\[2ex] B=-2 \end{array}$

لذلك، نحتاج فقط إلى إيجاد المعامل C. وللقيام بذلك، يجب علينا استبدال النقطة التي نعرف أنها تنتمي إلى الخط في معادلته:

$P(-4,3)$

$6x-2y+C=0 \ \xrightarrow{x=-4 \ ; \ y=3} \ 6\cdot (-4)-2\cdot 3+C=0$

$-24-6+C=0$

$-30+C=0$

$C=30$

إذن المعادلة الضمنية أو العامة أو الديكارتية للخط هي:

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{6x-2y+30=0}\quad \vphantom{\Bigl(}}$

الآن يمكننا تحديد المعادلة الصريحة لحل الخط للمجهول

$y$

من المعادلة الضمنية:

$6x-2y+30=0$

$-2y=-6x-30$

$y=\cfrac{-6x-30}{-2}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=3x+15}\quad \vphantom{\Bigl(}}$

ولذلك فإن ميل الخط يساوي 3 (الحد قبل المتغير المستقل

$x$

$m=3$

ومن قيمة ميل الخط، يمكننا حساب معادلة نقطة الميل للخط بصيغته:

$y-P_2=m(x-P_1)$

$y-3=3(x-(-4))$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y-3=3(x+4)}\quad \vphantom{\Bigl(}}$

التمرين 3

حدد ثلاث نقاط على السطر التالي، معبرًا عنها بمعادلة ضمنية أو عامة:

$4x+2y-8 = 0$

انظر الحل

لحساب نقطة على خط ما، نحتاج ببساطة إلى تعيين قيمة لأحد المتغيرات ثم إيجاد قيمة المتغير الآخر عند تلك النقطة.

نحسب النقطة الأولى عن طريق العمل

$x=0:$

$4\cdot 0+2y-8 = 0$

$2y = 8$

$y = \cfrac{8}{2}$

$y = 4$

$\bm{P_1(0,4)}$

ثم نجد نقطة ثانية تعطي قيمة أخرى للمتغير

$x,$

على سبيل المثال

$x=1:$

$4\cdot 1+2y-8 = 0$

$2y = 8-4$

$2y = 4$

$y = \cfrac{4}{2}$

$y = 2$

$\bm{P_2(1,2)}$

وأخيرًا، نحسب النقطة الثالثة عن طريق الحل

$x=2:$

$4\cdot 2+2y-8 = 0$

$2y = 8-8$

$2y = 0$

$y = \cfrac{0}{2}$

$y = 0$

$\bm{P_3(2,0)}$

التمرين 4

أوجد جميع معادلات الخط المحدد بالنقطة

$P$

والمتجه

$\vv{\text{v}}.$

$P(-1,4) \qquad \qquad \vv{\text{v}}=(-3,6)$

انظر الحل

أولًا، نجد المعادلة المتجهية للخط من صيغته:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(-1,4)+t\cdot (-3,6)} \quad \vphantom{\Bigl(}}$

ثانياً: نجد المعادلات البارامترية للخط من خلال الصيغة المقابلة له:

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-1-3t} \\[1.7ex] \bm{y=4+6t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

ونحدد أيضًا المعادلة المستمرة للخط باستخدام صيغته:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-(-1)}{-3}=\cfrac{y-4}{6}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x+1}}{\bm{-3}}\bm{=}\cfrac{\bm{y-4}}{\bm{6}}\quad \vphantom{\Biggl(}}$

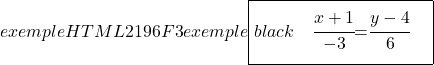
لننتقل الآن إلى إيجاد المعادلة الضمنية أو العامة للخط. للقيام بذلك، نعبر كسري المعادلة المستمرة:

$6\cdot (x+1)= -3 \cdot (y-4)$

$6x+6= -3y+12$

$6x+6+3y-12=0$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{6x+3y-6=0}\quad \vphantom{\Bigl(}}$

الآن يمكننا تحديد المعادلة الصريحة لحل الخط للمجهول

$y$

من المعادلة الضمنية:

$6x+3y-6=0$

$3y=-6x+6$

$y=\cfrac{-6x+6}{3}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=-2x+2}\quad \vphantom{\Bigl(}}$

ولذلك فإن ميل الخط يعادل -2 (الحد الذي يصاحب المتغير المستقل

$x$

$m=-2$

وبهذا يمكننا حساب معادلة نقطة الميل للخط بصيغته:

$y-P_2=m(x-P_1)$

$y-4=-2(x-(-1))$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y-4=-2(x+1)}\quad \vphantom{\Bigl(}}$

وأخيراً، لإيجاد المعادلة القطعية للخط، نحسب نقاط تقاطع الخط مع المحورين OX وOY ثم نستخدم صيغتها:

$y=-2x+2$

نقطة التقاطع مع محور الإحداثي السيني (المحور X)

$y=0$

$0=-2x+2$

$2x=2$

$x=\cfrac{2}{2} =1$

$\displaystyle \left(1, 0\right)$

نقطة التقاطع مع المحور y (المحور Y)

$x=0$

$y=-2\cdot 0+2$

$y=2$

$\displaystyle \left(0,2\right)$

$\cfrac{x}{a}+\cfrac{y}{b} = 1$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\cfrac{\bm{x}}{\bm{1}}+\cfrac{\bm{y}}{\bm{2}} \bm{= 1} \quad \vphantom{\Biggl(}}$

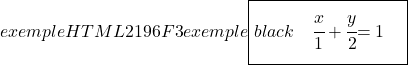
التمرين 5

أوجد معادلة الخط المستقيم الذي يمر بالنقطتين التاليتين:

$P_1 (4,-1) \qquad \qquad P_2(5,2)$

انظر الحل

وبما أننا نعرف بالفعل نقطتين على الخط، فإننا نطبق مباشرة صيغة معادلة الخط على نقطتين محددتين:

$y-y_1= \cfrac{y_2-y_1}{x_2-x_1} (x-x_1)$

الآن نعوض بالإحداثيات الديكارتية للنقاط في الصيغة:

$y-(-1)= \cfrac{2-(-1)}{5-4} (x-4)$

وأخيرًا، نحسب ميل الخط:

$y+1= \cfrac{3}{1} (x-4)$

$y+1= 3(x-4)$

وبالتالي فإن معادلة الخط الذي يمر عبر هاتين النقطتين هي:

$\bm{y+1= 3(x-4)}$

ما هي جميع معادلات الخط؟

معادلة المتجهات للخط

المعادلات البارامترية للخط

المعادلة المستمرة للخط

المعادلة الضمنية أو العامة للخط

معادلة صريحة للخط

معنى المعلمات م و ن

احسب ميل الخط

معادلة نقطة الميل للخط

المعادلة الكنسي أو القطاعية للخط

جميع معادلات الخط (الصيغ)

مثال لحساب معادلات الخط

معادلة خط مستقيم يمر بنقطتين

حل مسائل معادلات الخط

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

اترك تعليقاً إلغاء الرد