▷ كيفية حل جميع أنواع عدم التحديد (الحدود)

في هذه المقالة نوضح ما هو عدم التحديد. سوف تكتشف ما هي جميع أنواع عدم التحديد وكيفية حلها. بالإضافة إلى ذلك، ستتمكن من رؤية التمارين التي تم حلها خطوة بخطوة حول حدود الوظائف لجميع حالات عدم التحديد.

ما هي عدم التحديد؟

إن عدم التحديد، والتي تسمى أيضًا النماذج غير المحددة، هي تعبيرات رياضية تظهر في حساب حدود الدوال التي لم يتم تحديد نتيجتها. وبالتالي، لحل مشكلة عدم تعيين الحدود، من الضروري تطبيق إجراء أولي يعتمد على نوع الوظيفة.

أي أنه عندما نحصل على عدم التعيين، فهذا لا يعني أن النهاية غير موجودة أو أنه لا يمكن حلها، بل يعني أنه سيتعين علينا إجراء تغييرات على الدالة لإيجاد حل النهاية.

أنواع التحديدات

يتم تصنيف عدم التحديد أو الأشكال غير المحددة إلى الأنواع التالية:

اللانهاية اللانهاية ناقص اللانهاية (∞-∞)
عدد عدم التحديد بين الصفر (k/∞)
عدم التحديد الصفري بين الصفر (0/0)
عدم التحديد اللانهائي بين اللانهاية (∞/∞)
عدم التعيين 1 مرفوع إلى ما لا نهاية (1 ^∞ )
تم رفع عدم التحديد إلى الصفر (0 ⁰ )
عدم التحديد صفر لما لا نهاية (0·∞)
عدم التحديد صفر مرفوع إلى ما لا نهاية (0 ^∞ )
عدم التحديد اللانهائي وصل إلى الصفر (∞ ⁰ )

سنرى بعد ذلك كيفية حل جميع أنواع عدم التحديد.

اللانهائي ناقص اللاحتمية اللانهائية

الصيغة غير المعينة ما لا نهاية ناقص ما لا نهاية لا تساوي صفرًا، لأننا نطرح عددين كبيرين جدًا ولكننا لا نعرف أيهما أكبر. ولذلك فإن نتيجة الفرق بين اللانهاية تعتمد على ترتيب كل لانهاية.

$\infty-\infty$

إن حل هذا النوع من عدم التحديد ليس بالأمر السهل، لأنه اعتمادًا على نوع الوظيفة، يجب تطبيق إجراء أو آخر. لذا ننصحك بمشاهدة الشرح كاملاً في الرابط التالي:

➤ انظر: كيفية حل عدم التحديد ما لا نهاية ناقص ما لا نهاية

عدد عدم التحديد بين الصفر

يتم الحصول على عدم تعيين الثابت مقسومًا على صفر عند حذف مقام الدالة الكسرية.

$\cfrac{k}{0}$

ستكون نتيجة هذا النوع من الصيغة غير المحددة دائمًا أكثر لا نهائية، وأقل لا نهائية، وإلا فإن نهاية الدالة لن تكون موجودة. دعونا نرى كيف يتم حساب عدم التحديد هذا عن طريق حل النهاية كمثال:

$\displaystyle\lim_{x\to 0}\cfrac{-4}{x^2}=\cfrac{-4}{0^2}=\cfrac{-4}{0}=\infty$

لقد حصلنا على عدم تعيين عدد مقسومًا على صفر، لذا نحتاج إلى حساب الحدود الجانبية للدالة:

$\displaystyle\lim_{x\to 0^-}\cfrac{-4}{0^2}=\cfrac{-4}{(-0,001)^2}=\cfrac{-4}{+0}=-\infty$

$\displaystyle\lim_{x\to 0^+}\cfrac{-4}{0^2}=\cfrac{-4}{0,001^2}=\cfrac{-4}{+0}=-\infty$

➤ انظر: ما هي الحدود الجانبية؟

يعطي الحدان الجانبيان للدالة نفس النتيجة، لذا بحكم التعريف فإن حد الدالة عندما تميل x إلى 0 يعطي سالب ما لا نهاية:

$\displaystyle\lim_{x\to 0^-}f(x)=\lim_{x\to 0^+}f(x)=-\infty \ \longrightarrow \ \lim_{x\to 0}f(x)=-\infty$

لاحظ أنه إذا أعطت النهايات الجانبية قيمًا مختلفة، فلن تكون نهاية الدالة عند هذه النقطة موجودة.

صفر بين الصفر عدم التحديد

الحد غير المحدد صفر مقسومًا على صفر شائع جدًا ويتم الحصول عليه في الدوال التي تحتوي على كسور يتم فيها إلغاء البسط والمقام.

$\cfrac{0}{0}$

يتم حل هذا النوع من الحدود غير المحددة بشكل مختلف اعتمادًا على الوظيفة. على سبيل المثال، إذا كانت الدالة لها جذور، فيجب تنفيذ خطوات مختلفة. يمكنك رؤية الحلول المختلفة لهذا النوع من عدم التحديد في الرابط التالي:

➤ انظر: كيفية حل عدم التحديد الصفري بين الصفر

اللانهائي بين اللانهائي

عادةً ما يحدث عدم التحديد اللانهائي بين اللانهاية في الحدود اللانهائية للوظائف ذات الكسور. على الرغم من أن عدم التعيين هو حاصل قسمة لا نهائيتين، إلا أن النتيجة لا يجب بالضرورة أن تكون ما لا نهاية.

$\cfrac{\infty}{\infty}$

يتم حل هذا النوع من النموذج غير المحدد عن طريق المقارنة. وهذا يعني أنه يتم ملاحظة درجة البسط ودرجة المقام، واعتمادًا على أيهما أكبر، تكون نتيجة النهاية واحدة أو أخرى. يمكنكم مشاهدة جميع الحالات في الرابط التالي:

➤ انظر: تمارين محلولة على الحدود اللانهائية بين ما لا نهاية

عدم التعيين 1 مرفوع إلى ما لا نهاية

رياضيا، قد يعتقد المرء أن 1 إلى ما لا نهاية يعطي 1، لأن أي قوة 1 تساوي 1. ومع ذلك، هذا المصطلح هو عدم تحديد، وبالتالي، لا يمكن للمرء أن يستنتج نتائجه بسهولة.

$1^{\infty}$

يتم حساب هذا النوع من عدم التحديد من خلال تطبيق الصيغة التالية:

$\displaystyle\lim_{x\to+\infty}f(x)^{g(x)}=\lim_{x\to+\infty}e^{g(x)\cdot [f(x)-1]}$

على سبيل المثال، النهاية التالية غير محددة لأنها تعطي قوة اللانهاية:

$\displaystyle\lim_{x\to+\infty}\left(1-\frac{1}{x}\right)^x=\left(1-\frac{1}{+\infty}\right)^{+\infty}=(1-0)^{+\infty}=1^{+\infty}$

لذلك يجب علينا استخدام الصيغة لهذا النوع من عدم التحديد:

$\displaystyle\lim_{x\to+\infty}e^{x\cdot\left[1-\frac{1}{x}-1\right]}=\lim_{x\to+\infty}e^{x\cdot\left[-\frac{1}{x}\right]}=\lim_{x\to+\infty}e^{-1}=\frac{1}{e}$

وبذلك نكون قد توصلنا بالفعل إلى النهاية غير المحددة المرفوعة إلى ما لا نهاية.

جلبت عدم التحديد الصفر إلى الصفر

يظهر عدم التحديد الصفري للقوة الصفرية ضمن حدود الوظائف المعقدة.

$0^0$

لحل هذا النوع من الحد غير المحدد، يجب عليك استخدام خاصية الحد التالية:

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

على سبيل المثال، النهاية التالية تعطي الصيغة غير المحددة 0 أس 0:

$\displaystyle\lim_{x\to +\infty}\left(\frac{1}{x}\right)^{\frac{1}{x}}=\left(\frac{1}{+\infty}\right)^{\frac{1}{+\infty}}=0^0$

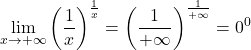
لكن إذا طبقنا اللوغاريتمات على النهاية، فيمكننا إيجاد قيمتها:

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}\left(\frac{1}{x}\right)^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln\left(\frac{1}{x}\right)}}=\\[5ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln\left(\frac{1}{x}\right)}{x}}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln1-\ln x}{x}}}=\\[5ex]=\displaystyle e^{^{\displaystyle\lim_{x\to +\infty}\frac{-\ln x}{x}}}=e^{^{\displaystyle\frac{-\infty}{+\infty}}}=e^0=1\end{array}$

عدم التحديد الصفري لللانهاية

من الصعب مواجهة عدم تعيين حاصل ضرب الصفر واللانهاية ، لكن هذا لا يعني أنه من السهل تحديده.

$0\cdot \infty$

لا توجد طريقة واحدة لحل هذا النوع من عدم التحديد، ولكنها تعتمد على نوع الوظيفة. وفي هذه الحالة يجب علينا تحويل الدالة إلى عدم التحديد اللانهائي مقسومًا على ما لا نهاية أو عدم التعيين صفر مقسومًا على صفر، ومن هناك نطبق طرق الحل التي رأيناها أعلاه لكل عدم تعيين.

فإذا كانت نهاية إحدى الدالتين 0 وكانت نهاية الدالة الأخرى ∞:

$\displaystyle\lim_{x\to a}f(x)=0\qquad\lim_{x\to a}g(x)=\infty$

يمكننا تحويل هذا النوع إلى أجل غير مسمى عن طريق إجراء التغييرات التالية:

$\displaystyle\lim_{x\to a}f(x)\cdot g(x)\begin{cases}\displaystyle\lim_{x\to a}\frac{f(x)}{\displaystyle\frac{1}{g(x)}}=\frac{0}{0}\\[10ex]\displaystyle\lim_{x\to a}\frac{g(x)}{\displaystyle\frac{1}{f(x)}}=\frac{\infty}{\infty}\end{cases}$

دعونا نرى كيفية القيام بذلك عن طريق حل نهاية غير محددة كمثال:

$\displaystyle\lim_{x\to +\infty}e^{-x}\cdot x=e^{-\infty}\cdot (+\infty)=0\cdot \infty$

نعمل على الدالة للحصول على عدم التحديد اللانهائي على اللانهاية ثم نجد النهاية:

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}e^{-x}\cdot x=\lim_{x\to +\infty}\frac{x}{\displaystyle\frac{1}{e^{-x}}}=\\[6ex]=\displaystyle \lim_{x\to +\infty}\frac{x}{e^x}=\frac{+\infty}{e^{+\infty}}=\frac{+\infty}{+\infty}=0\end{array}$

رفع عدم التحديد الصفر إلى ما لا نهاية

من الصعب بعض الشيء فهم عدم التعيين صفر مرفوعًا إلى ما لا نهاية ، لأننا نرفع عددًا صغيرًا جدًا إلى عدد كبير جدًا.

$0^{\infty}$

عند الحصول على هذه النماذج غير المحددة، يجب استخدام الصيغة التالية:

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

دعونا نحل مثالاً لفهم كيفية حساب هذا النوع من عدم التحديد بشكل أفضل:

$\begin{array}{l}\displaystyle\lim_{x\to 0^+}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to 0^+}\frac{1}{x}\cdot \ln(x)}}=\\[3.5ex]\displaystyle =e^{^{\displaystyle\frac{1}{0^+}\cdot \ln(0^+)}}=e^{+\infty\cdot (-\infty)}\\[3ex]\displaystyle =e^{-\infty}=\frac{1}{e^{+\infty}}=0\end{array}$

عدم التحديد اللانهائي وصل إلى الصفر

عادة، أي قوة مرفوعة إلى الصفر تعطي 1، ومع ذلك، فإن عدم تحديد اللانهاية المرفوعة إلى الصفر ليس بالضرورة أن يكون بهذه الطريقة.

$\infty^0$

كما هو الحال في عدم التحديد صفر مرفوع إلى صفر وصفر مرفوع إلى ما لا نهاية، لحل هذا النوع من النهاية غير المحددة، من الضروري تطبيق اللوغاريتمات:

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

دعونا نرى كيف يتم حل هذا النوع من الحدود غير المحددة عن طريق حساب مثال خطوة بخطوة:

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln(x)}}=\\[3ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln(x)}{x}}}=e^{^{\displaystyle\frac{\ln(+\infty)}{+\infty}}}=\\[3ex]\displaystyle =e^{^{\displaystyle\frac{+\infty}{+\infty}}}=e^0=1\end{array}$

أنواع عدم التعيين (الحدود غير المحددة)

ما هي عدم التحديد؟

أنواع التحديدات

اللانهائي ناقص اللاحتمية اللانهائية

عدد عدم التحديد بين الصفر

صفر بين الصفر عدم التحديد

اللانهائي بين اللانهائي

عدم التعيين 1 مرفوع إلى ما لا نهاية

جلبت عدم التحديد الصفر إلى الصفر

عدم التحديد الصفري لللانهاية

رفع عدم التحديد الصفر إلى ما لا نهاية

عدم التحديد اللانهائي وصل إلى الصفر

اترك تعليقاً إلغاء الرد