ضرب المتجه بعدد

تشرح هذه الصفحة كيفية ضرب متجه بعدد حقيقي (أو سلمي) عدديًا ورسوميًا. بالإضافة إلى ذلك، ستجد أيضًا أمثلة وتمارين محلولة لضرب متجه بكمية قياسية. وأخيرا، تم أيضا شرح خصائص هذا النوع من العمليات مع المتجهات.

كيف يمكنك ضرب المتجه بعدد حقيقي؟

وبالتالي فإن نتيجة ضرب المتجه في عدد يؤدي إلى ظهور متجه جديد يتمتع بالخصائص التالية:

• نتيجة ضرب المتجه بكمية قياسية تنتج متجهًا جديدًا بنفس اتجاه المتجه الأصلي.
• بالإضافة إلى ذلك، سيكون للمتجه الجديد نفس الاتجاه إذا كان الرقم موجبًا.
• أو سيكون له معنى معاكس إذا كان الرقم سالبا.
• حجم المتجه الناتج يعادل حجم المتجه الأصلي مضروبًا في العددية.

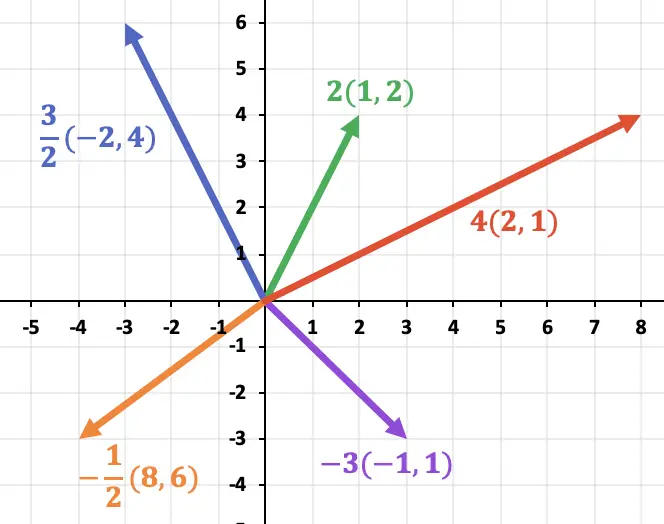
في الرسم البياني التالي يمكنك أن ترى كيف يتم الحفاظ على اتجاه المتجه بغض النظر عن إشارة العددية. ومن ناحية أخرى، فإن اتجاه المتجه يعتمد على إشارة العدد الذي يضربه.

علاوة على ذلك، في الرسم البياني التالي، نرى بوضوح أن مقدار متجه حاصل الضرب الناتج يساوي مقدار المتجه الأصلي مضروبًا في العددية.

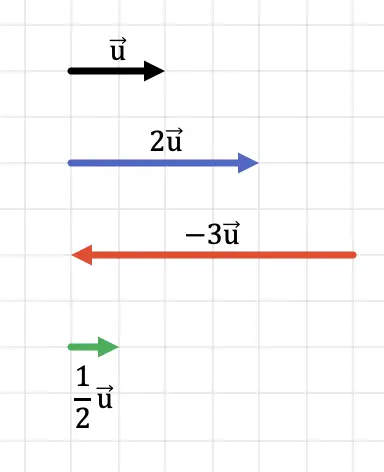
من الواضح أننا إذا ضربنا المتجه بعدد أكبر من 1، فإن النتيجة هي متجه بطول أكبر (ذو معامل أكبر). من ناحية أخرى، إذا ضربنا المتجه بعدد أقل من 1، فستكون النتيجة متجهًا بطول أقصر (معامل أصغر).

ملاحظة: لا تخلط بين حاصل ضرب المتجه والرقم مع حاصل الضرب النقطي للمتجهات . على الرغم من أنهما يحملان اسمًا مشابهًا، إلا أنهما مفهومان مختلفان تمامًا.

مثال على منتج المتجه بواسطة العددية

بعد ذلك، سنرى مثالًا رقميًا لكيفية حساب حاصل ضرب متجه وعدد:

• اضرب المتجه التالي بـ 4:

كما رأيت، هذا النوع من عمليات المتجهات ليس معقدًا للغاية، لأنه لا يتعين عليك إجراء الكثير من الحسابات.

ومع ذلك، هناك عمليات متجهة أكثر تعقيدًا، مثل جمع المتجهات وطرح المتجهات. إذا كنت قد فهمت بالفعل كيفية حساب حاصل ضرب متجه وكمية قياسية، فنوصيك بالانتقال إلى المستوى التالي ومعرفة كيفية حل جمع المتجهات وطرح المتجهات ، حيث أن هذه عمليات أكثر صعوبة إلى حد ما، وفي الواقع، يتم استخدامها أكثر من ذلك بكثير (فهي أكثر أهمية).

خصائص ضرب المتجه بعدد

حاصل ضرب متجه وعدد له الخصائص التالية:

• خاصية الدمج : عندما يتم ضرب المتجه بأكثر من رقم، لا يهم ترتيب الضرب.

• خاصية التوزيع فيما يتعلق بجمع وطرح المتجهات:

• خاصية التوزيع فيما يتعلق بإضافة الكميات:

• العنصر المحايد : من الواضح أن أي متجه مضروبًا في 1 يعطي المتجه نفسه:

حل مسائل ضرب المتجه بمقدار قياسي

التمرين 1

احسب تحليلياً نتيجة حاصل ضرب المتجه التالي بمقدار 3:

للعثور على المنتج، يجب عليك ضرب كل إحداثيات المتجه بـ 3:

تمرين 2

اضرب المتجه التالي في 6 وابحث عن وحدته:

نقوم أولاً بضرب المتجه في العددية:

توجد الآن طريقتان لحساب حجم المتجه الذي تم الحصول عليه. الأول هو إيجاد مقدار المتجه الأصلي، ثم ضربه في 6:

والطريقة الثانية هي حساب حجم المتجه الذي تم الحصول عليه في الضرب مباشرة:

بحيث يظهر في كلا الإجراءين أن النتيجة لا تعتمد على الطريقة التي يتم من خلالها حساب المعامل.

التمرين 3

من المتجهات التالية:

احسب العمليات التالية جبريا:

بعد ذلك، حدد ما إذا كانت المتجهات الناتجة لها نفس اتجاه واتجاه المتجه الأصلي، ورتبها من الأقصر إلى الأطول.

نقوم أولا بحساب الضرب:

ولذلك، فإن المتجهات مضروبة في الأعداد الموجبة لها نفس اتجاه واتجاه المتجه الأصلي. والمتجهات مضروبة في الأعداد السالبة لها نفس الاتجاه ولكن الاتجاه المعاكس للمتجه الأصلي.

متجهات لها نفس الاتجاه ونفس الاتجاه:

و

المتجهات التي لها نفس الاتجاه ولكن معنى مختلف:

وأخيرًا، يجب علينا ترتيب المتجهات وفقًا لأطوالها، أو ما يعادل وحدتها. سيكون المتجه ذو الطول الأطول (أو الوحدة الأكبر) هو المتجه الذي تم ضربه بعدد أكبر (بالقيمة المطلقة)، وسيكون المتجه الأقصر طولًا (أو أصغر وحدة) هو المتجه الذي تم ضربه بعدد أصغر الرقم (بالقيمة المطلقة). وبالتالي فإن ترتيب الأطوال هو:

لاحظ أن الطول أو المقياس لا يعتمد على إشارة العدد المضروب، لأن اتجاه المتجه لا يعدل معامله.

التمرين 4

خذ بعين الاعتبار المتجهين التاليين:

احسب العملية التالية:

نقوم أولاً بحل ضرب المتجهات بالأرقام:

ثم نطرح المتجهات:

التمرين 5

قم بإجراء عمليات ضرب المتجهات التالية بالكميات القياسية ورسم النتائج بيانيًا:

نقوم أولاً بضرب المتجهات في الكميات القياسية الحقيقية:

أخيرًا، بمجرد قيامنا بحساب المتجهات، فإننا نمثلها في الرسم البياني: