الطرح المتجه

في هذه الصفحة، ستشاهد كيفية طرح متجهين، بيانيًا وعدديًا. لطرحها بيانيًا هناك ثلاث طرق: متوازي الأضلاع، والمثلث، والمضلع. هنا يمكنك التمييز بين مزايا وعيوب كل طريقة. بالإضافة إلى ذلك، ستجد أمثلة وتمارين ومسائل تم حلها خطوة بخطوة.

كيفية طرح اثنين من المتجهات بيانيا؟

هناك عدة طرق لطرح المتجهات هندسيًا. من الواضح أنه مع كل منهم يتم الحصول على نفس النتيجة، لكننا سنشرح لك جميع الطرق حتى تتمكن من اختيار الطريقة التي تفضلها. 👌

لطرح متجهين فقط، هناك إجراءان رسوميان: طريقة متوازي الأضلاع وطريقة المثلث . ومع ذلك، إذا أردنا حل عملية طرح 3 متجهات أو أكثر، نحتاج إلى استخدام طريقة المضلع .

لذا، وبدون مزيد من اللغط، لديك شرح لكل هذه الطرق أدناه.

طريقة أو قاعدة متوازي الأضلاع

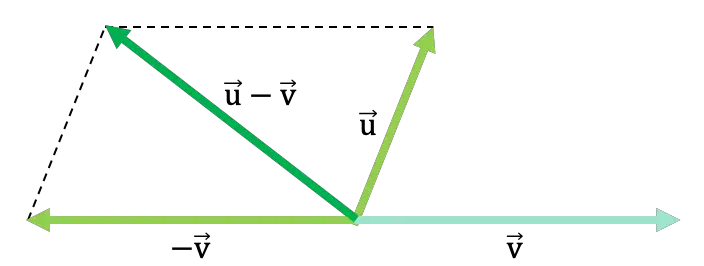
قاعدة متوازي الأضلاع أو طريقة متوازي الأضلاع هي إجراء يسمح لك بالعثور على طرح متجهين من خلال تمثيلهما الرسومي بطريقة بسيطة جدًا. الخطوات التي يجب اتباعها لتطبيق هذه العملية هي كما يلي:

أولاً، نمثل المتجهين على الرسم البياني ونضعهما في نفس نقطة التطبيق، أي أننا نضع أصول كلا المتجهين في نفس النقطة.
ثانيًا، نرسم المتجه المعاكس للمتجه الذي يتم طرحه في العملية، أو بعبارة أخرى، نعكس المتجه الذي يتم طرحه.
ثم نرسم خطًا موازيًا للمتجه الذي تغير الإشارة في نهاية المتجه المضاف. ونكرر العملية مع المتجه الآخر. حتى نحصل على رسم متوازي الأضلاع (ومن هنا اسم القاعدة).
وأخيرًا، ستكون نتيجة الطرح هي المتجه الذي ينتقل من الأصل المشترك للمتجهين إلى النقطة التي يتقاطع فيها الخطان المتوازيان.

خذ بعين الاعتبار المثال العام التالي الذي يتم فيه طرح متجهين باستخدام طريقة متوازي الأضلاع:

طريقة المثلث أو القاعدة

طريقة المثلث هي إجراء آخر يمكن من خلاله طرح متجهين من الرسم البياني الخاص بهما. وفي هذه الحالة فإن الخطوات التي يجب اتباعها هي:

ضع المتجهين في نفس نقطة التطبيق، أي أن المتجهين لهما نفس نقطة الأصل.
نتيجة طرح المتجه هي القطعة التي تمتد من نهاية المتجه الطرح إلى نهاية المتجه الآخر. إذا نظرت عن كثب، ستجد أن المثلث قد اكتمل بطرح المتجهين وطرح المتجه.

فيما يلي مثال على طرح المتجهات باستخدام طريقة المثلث:

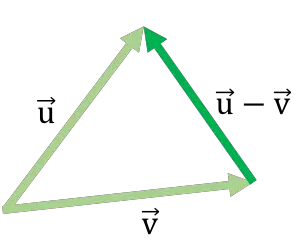
تشبه طريقة طرح المتجهات هذه طريقة الرأس والذيل المستخدمة لإضافة المتجهات .

طريقة المضلع

بعد أن رأينا كيفية حل عملية طرح متجهين بيانيًا، سنرى كيف يتم ذلك عندما يكون لدينا أكثر من متجهين.

عندما تريد طرح ثلاثة متجهات أو أكثر، هناك أسلوب لتسريع العملية الحسابية وطرح جميع المتجهات مرة واحدة. تسمى هذه التقنية بطريقة المضلع وتتكون من تطبيق طريقة إضافة المتجهات من الرأس إلى الذيل بشكل متتابع.

الآن ربما تفكر: إضافة ناقلات؟ لقد تم تصحيحه بشكل غير صحيح…حسنا لا! ايه ايه

اتضح أن طرح متجهين هو نفس إضافة متجه بالإضافة إلى المتجه المعاكس (أو السلبي) للمتجه الطرح. ويرجع ذلك إلى خصائص الجمع والطرح للمتجهات:

$\vv{a} - \vv{b} =\vv{a} +(-\vv{b})$

ولذلك، فإن الخطوات التي يتعين علينا اتباعها لطرح 3 متجهات أو أكثر بطريقة المضلع هي:

أولًا، علينا إيجاد المتجه العكسي لكل متجه طرح. الأمر بسيط مثل عكس اتجاه واتجاه جميع المتجهات التي تم طرحها.
ثم نضع كل متجه متقابل بجوار المتجه الذي لا تطرحه، واحدًا تلو الآخر. بحيث يتطابق أصل المتجه مع نهاية متجه آخر.
وأخيرًا، نتيجة طرح المتجه هي المتجه الذي يتم الحصول عليه من خلال ربط بداية المتجه الأول بنهاية المتجه الأخير.

انظر إلى المثال التالي حيث يتم إجراء عملية طرح باستخدام 4 متجهات:

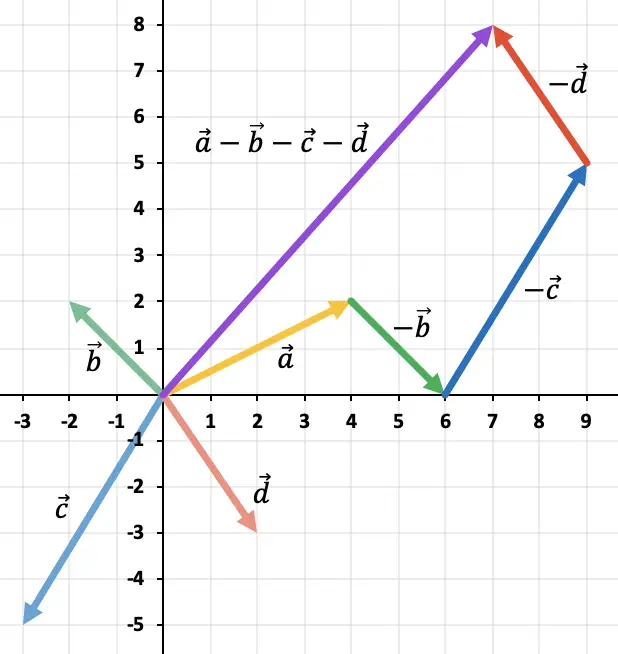
لاحظ أنه للعثور على المتجه المعاكس للمتجه، يجب أن تتغير الإشارة لعنصري المتجه المذكور.

كيف تحسب عدديا طرح متجهين؟

بمجرد أن نعرف بالفعل كيفية طرح المتجهات من الرسم البياني، سنرى كيفية حساب طرح المتجهات عدديًا أو جبريًا.

لطرح متجهين عدديًا، يجب عليك طرح مكونات كل منهما. أو بمعنى آخر، يتم طرح إحداثيات X للمتجهين من بعضهما البعض وكذلك الأمر مع إحداثيات Y.

$\vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)$

$\vv{\text{u}} - \vv{\text{v}} = (\text{u}_x - \text{v}_x \ , \ \text{u}_y - \text{v}_y)$

على سبيل المثال، الطرح بين المتجهات

$\vv{\text{u}} = (4,1)$

$\vv{\text{v}}=(2, 3)$

شرق:

$\vv{\text{u}} = (4,1) \qquad \vv{\text{v}}=(2, 3)$

$\begin{aligned} \vv{\text{u}} - \vv{\text{v}}& =(4,1) -(2, 3) \\[2ex] & = (4-2,1-3) \\[2ex] & = \bm{(2,-2)} \end{aligned}$

حل مسائل طرح المتجهات

التمرين 1

حساب طرح المتجهات بيانيا

$\vv{a}$

أقل

$\vv{b}:$

انظر الحل

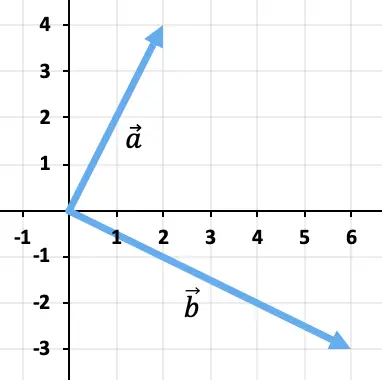
لطرح المتجهين، سنستخدم طريقة المثلث. النقاط موضوعة بالفعل في نفس نقطة التطبيق (أصل الإحداثيات)، وبالتالي فإن نتيجة الطرح ستكون المتجه الذي يبدأ من نهاية

$\vv{b}$

في نهاية

$\vv{a}.$

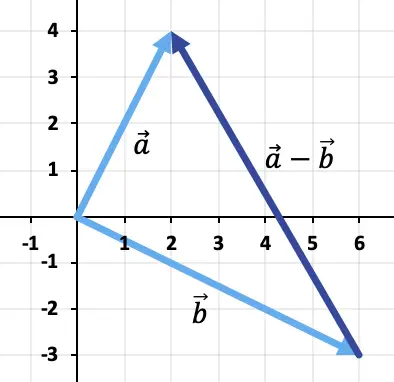
تمرين 2

العثور على طرح المتجهات بيانيا

$\vv{a}$

أقل

$\vv{b}:$

انظر الحل

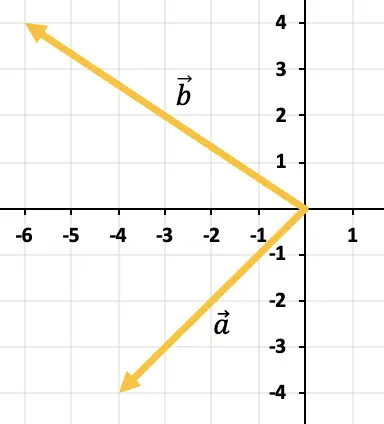
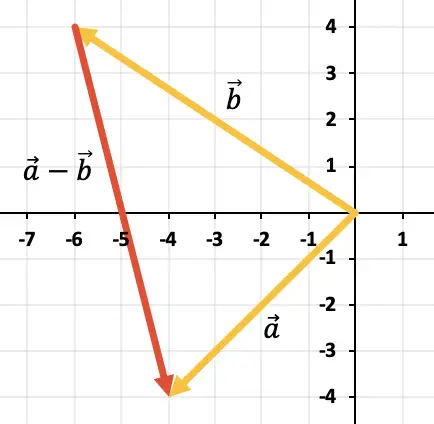
لطرح المتجهين، سنستخدم قاعدة المثلث. النقاط موضوعة بالفعل في نفس نقطة التطبيق (في بداية المحور X والمحور Y)، وبالتالي فإن نتيجة الطرح ستكون المتجه الذي يبدأ من نهاية

$\vv{b}$

في نهاية

$\vv{a}.$

التمرين 3

حل عملية المتجهات التالية بيانياً:

$\vv{a}-\vv{b}-\vv{c}-\vv{d}-\vv{e}$

انظر الحل

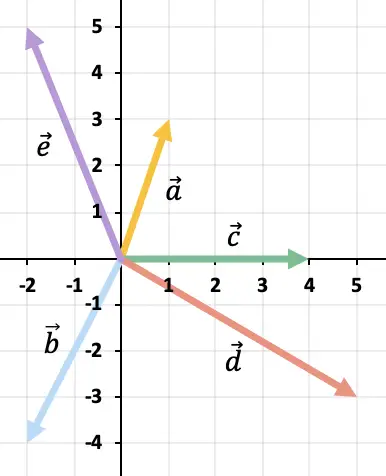
نظرًا لوجود أكثر من متجهين، سنستخدم قاعدة المضلع لحل عملية طرح المتجهات. للقيام بذلك، علينا تمثيل المتجهات المعاكسة للمتجهات المتبقية واحدًا تلو الآخر. وستكون النتيجة المتجه الذي يبدأ من أصل المتجه

$\vv{a}$

إلى حيث ينتهي المتجه المعاكس الأخير.

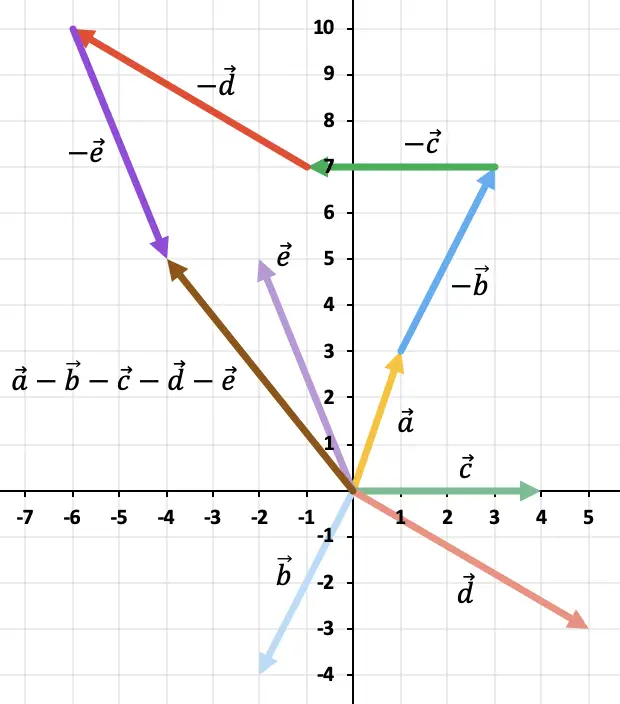
التمرين 4

حدد عددياً نتيجة طرح المتجهات التالية:

$\vv{a}=(-1,5) \qquad \vv{b}=(3,-2)$

$\vv{a}-\vv{b}$

انظر الحل

لطرح متجهين عدديًا، يجب عليك طرح إحداثيات كل منهما:

$\begin{aligned} \vv{a}-\vv{b}& =(-1,5)-(3,-2) \\[2ex] & = (-1-3 ,5-(-2))\\[2ex] & = (-4 ,5+2)\\[2ex] & =\bm{(-4,7)} \end{aligned}$

التمرين 5

حل تحليليا عملية المتجهات التالية:

$\vv{a}=(2,4) \qquad \vv{b}=(-1,4)\qquad \vv{c}=(0,2)\qquad \vv{d}=(3,-7)$

$\vv{a}-\vv{b} -\vv{c}-\vv{d}$

انظر الحل

لطرح المتجهات عدديًا (أو تحليليًا)، يجب علينا طرح مكوناتها الخاصة:

$\begin{aligned} \vv{a}-\vv{b}-\vv{d}-\vv{d}& =(2,4)-(-1,4)-(0,2)-(3,-7) \\[2ex] & =(3,0)-(0,2)-(3,-7) \\[2ex] & =(3,-2)-(3,-7) \\[2ex]& =\bm{(0,5)} \end{aligned}$

كيفية طرح اثنين من المتجهات بيانيا؟

طريقة أو قاعدة متوازي الأضلاع

طريقة المثلث أو القاعدة

طريقة المضلع

كيف تحسب عدديا طرح متجهين؟

حل مسائل طرح المتجهات

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

اترك تعليقاً إلغاء الرد