طريقة المربعات الصغرى هي أداة رياضية لإيجاد أفضل خط مستقيم يتوافق مع مجموعة من النقاط . نشرحها لك بطريقة بسيطة:
تخيل أن لديك مجموعة من النقاط على رسم بياني متناثرة هنا وهناك. تريد العثور على خط مستقيم “يناسب” هذه النقاط بشكل أفضل، وذلك لتقليل المسافة بين الخط والنقاط . هذه هي الفكرة وراء طريقة المربعات الصغرى.
تستخدم الطريقة صيغة لحساب معادلة الخط التي تقلل مجموع مربعات الاختلافات بين النقاط والخط. أي أنه يبحث عن الخط الذي يحتوي على أصغر “انحراف” عن النقاط.
بعبارات بسيطة، تعد طريقة المربعات الصغرى مفيدة لتحليل البيانات التي تم الحصول عليها أثناء التحقيق، بهدف التعبير عن سلوكها بطريقة خطية، مما يقلل من أخطاء المعلومات المسروقة.
من الذي ابتكر طريقة المربعات الصغرى؟
تُنسب طريقة المربعات الصغرى، وهي أداة أساسية في الإحصاء وتحليل البيانات، إلى عالم الرياضيات الألماني كارل فريدريش غاوس ، الذي اقترحها عام 1794. إلا أن غاوس لم ينشرها حتى عام 1809 .
ومن المثير للاهتمام أن عالم الرياضيات الفرنسي أندريان ماري ليجيندر نشر نسخة مماثلة في عام 1805 ، وقام بتطويرها بشكل مستقل.
ساعد كلا علماء الرياضيات في إنشاء هذه الطريقة التي تم استخدامها على نطاق واسع في مختلف التخصصات لملاءمة النماذج مع البيانات المرصودة وإجراء تنبؤات دقيقة.
صيغة المربعات الصغرى
مما لا شك فيه، لفهم ما تنطوي عليه هذه الطريقة، من الضروري شرح صيغتها وعملية تنفيذها. فيما يلي شرح تفصيلي لصيغة المربعات الصغرى:
عرف المشكلة
لنفترض أن لديك مجموعة بيانات تحتوي على متغيرين، متغير مستقل (x) ومتغير تابع (y)، وتريد ملاءمة خط مستقيم لهذه البيانات.
الهدف هو إيجاد قيم معاملات معادلة الخط (التقاطع والمنحدر) مما يقلل مجموع مربعات الفروق بين القيم الحقيقية لـ y، والقيم التي تنبأ بها خط مجهز.
احسب معادلة الخط
معادلة الخط لها الصيغة y = mx + b، حيث m هو الميل وb هو تقاطع y. صيغة المربعات الصغرى لحساب قيم myb هي:
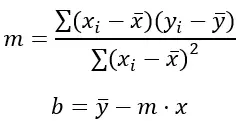
ذهب:
Σ يمثل مجموع القيم.
x i و y i هي قيم المتغيرات x و y على التوالي لكل نقطة بيانات.
x̄ و ų هما متوسطات قيم x و y على التوالي.
(x i – x̄) و (y i – ti) هي الاختلافات بين قيم x و y ووسائط كل منهما.
(x i – x̄) 2 هو مربع الفرق بين قيمة x ووسطها.
تفسير النتائج
بمجرد حساب قيمتي m وb باستخدام الصيغة، يمكنك استخدامها للحصول على معادلة الخط المجهز. على سبيل المثال، إذا كان لديك m = 2 وb = 3، فإن معادلة الخط الملائم ستكون y = 2x + 3. وهذا يسمح لك بعمل تنبؤات أو تقديرات لقيم y لقيم مختلفة لـ x على أساس الحق المعدل.
متى يتم استخدام طريقة المربعات الصغرى؟
ربما ستسأل نفسك متى يتم استخدام هذه الطريقة؟ إنه مفيد جدًا في المواقف المختلفة! على سبيل المثال، عندما تريد تحليل البيانات التجريبية أو البحثية للعثور على علاقة أو اتجاه .
لنفترض أنك تحقق في العلاقة بين سعر المنزل ومساحته بالمتر المربع. يمكنك استخدام طريقة المربعات الصغرى للعثور على الخط المستقيم الذي يناسب البيانات بشكل أفضل ويعطيك فكرة واضحة عن هذه العلاقة.
كما أنها تستخدم في الاقتصاد لنمذجة المتغيرات والتنبؤ بها مثل الطلب على المنتج أو سلوك السعر . بالإضافة إلى ذلك، في الهندسة، يتم تطبيق طريقة المربعات الصغرى لتناسب النماذج الرياضية لاختبار أو محاكاة البيانات.
تعتبر طريقة المربعات الصغرى أداة قوية ومتعددة الاستخدامات تستخدم في العديد من مجالات الدراسة والعمل على تحليل البيانات وإيجاد العلاقات المهمة.
تطبيقات طريقة المربعات الصغرى في نظريات أخرى
بالإضافة إلى استخدامها في حد ذاتها، فإن طريقة المربعات الصغرى مفيدة جدًا في النظريات الأخرى. دعونا نرى المزيد عن هذا الموضوع أدناه.
نظرية الانحدار
ويستخدم على نطاق واسع في نظرية الانحدار للعثور على أفضل خط يناسب مجموعة من البيانات . على سبيل المثال، يمكنك استخدامه لتحليل العلاقة بين ارتفاع النبات وكمية الضوء التي يتلقاها لتحديد كيفية نمو النبات في ظروف الإضاءة المختلفة.
الاستيفاء النظرية
في هذه الحالة، يتم أيضًا تطبيق طريقة المربعات الصغرى في نظرية الاستيفاء للعثور على دالة متعددة الحدود التي تناسب مجموعة من النقاط بشكل أفضل. على سبيل المثال، يمكنك استخدامه لتقريب مسار جسم متحرك بناءً على بيانات الموقع والوقت.
نظرية تركيب المنحنى
يتم استخدامه في نظرية ملائمة المنحنى للعثور على منحنى يناسب مجموعة من البيانات . وهذا مفيد في تطبيقات مثل نمذجة البيانات المناخية للتنبؤ بتغير المناخ أو التنبؤ بمسار المقذوف.
نظرية تحليل فورييه
في نظرية تحليل فورييه، يتم استخدام طريقة المربعات الصغرى لتقريب دالة دورية من سلسلة من البيانات المنفصلة . وينطبق هذا على تشوير البيانات وضغط الصورة والصوت.
نظرية الانحدار غير الخطية
أخيرًا، يتم أيضًا تطبيق طريقة المربعات الصغرى في نظرية الانحدار غير الخطي للعثور على أفضل منحنى يناسب مجموعة بيانات لا تتبع علاقة خطية . على سبيل المثال، يمكنك استخدامه لتحليل كيفية تأثير تركيز المادة الكيميائية على معدل التفاعل.
مثال على طريقة المربعات الصغرى
لفهم كيفية تطبيق طريقة المربعات الصغرى بشكل أفضل، دعونا نلقي نظرة على المثال أدناه.
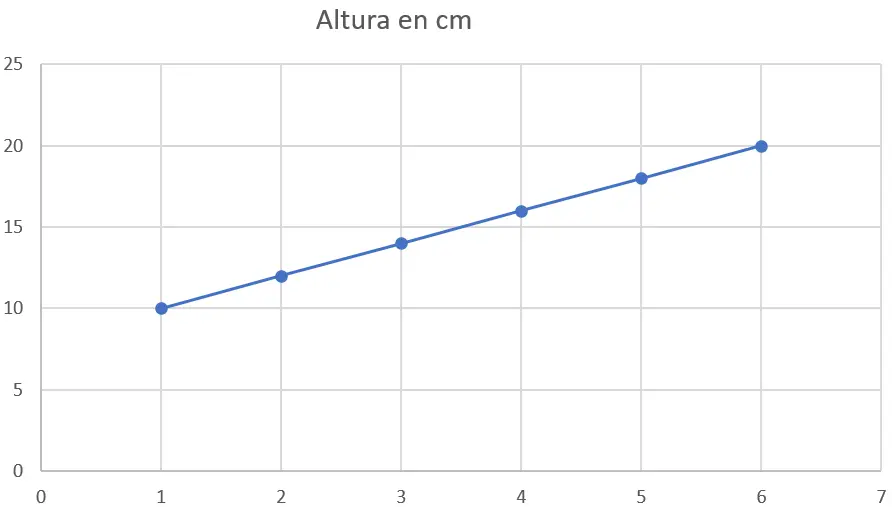
لنفترض أن لديك بيانات الارتفاع التالية (بالسنتيمتر) للنبات في أسابيع مختلفة:
| أسبوع | الارتفاع بالسنتيمتر |
| 1 | عشرة |
| 2 | 12 |
| 3 | 14 |
| 4 | 16 |
| 5 | 18 |
| 6 | عشرين |
تريد العثور على أفضل خط مستقيم يناسب هذه البيانات للتنبؤ بارتفاع النبات في المستقبل.
الخطوة 1 : الرسم البياني للبيانات
أول شيء يجب فعله هو رسم البيانات على مخطط التشتت. سيمثل المحور السيني الأسابيع وسيمثل المحور الصادي الارتفاع بالسنتيمتر. هنا هو الرسم البياني:
الخطوة 2 : تطبيق طريقة المربعات الصغرى
تسعى طريقة المربعات الصغرى إلى إيجاد خط يقلل مجموع مربعات الاختلافات بين البيانات الفعلية والقيم التي يتنبأ بها الخط. في هذه الحالة، يتم تمثيل الخط بمعادلة الخط: y = mx + b، حيث “y” هو الارتفاع، و”x” هو الأسابيع، و”m” هو ميل الخط و”b” هو تقاطع y.
للعثور على قيمتي “m” و”b” التي تقلل مجموع مربعات الاختلافات، يتم استخدام الصيغ التالية:
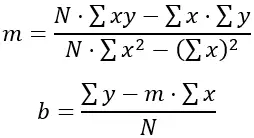
حيث N هو عدد نقاط البيانات (6 في هذه الحالة)، Σxy هو مجموع الأسابيع مضروبًا في الارتفاعات، Σx هو مجموع الأسابيع، Σy هو مجموع الارتفاعات، وΣx 2 هو مجموع مربعات الأسابيع .
وبتطبيق هذه الصيغ على بيانات الارتفاع نحصل على:
Σxy = 1 10 + 2 12 + 3 14 + 4 16 + 5 18 + 6 20 = 630
Σس = 1 + 2 + 3 + 4 + 5 + 6 = 21
Σy = 10 + 12 + 14 + 16 + 18 + 20 = 90
Σx 2 = 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 = 91
استبدال هذه القيم في الصيغتين “m” و”b”:
م = (6 · 630 – 21 · 90) ÷ (6 · 91 – 21 2 ) ≈ 2.07
ب = (90 – 2.07 · 21) ÷ 6 ≈ 3.24
ولذلك فإن معادلة الخط المستقيم الذي يتوافق مع بيانات الارتفاع هي: y.