▷ تكوين الوظائف (أو الوظيفة المركبة)

في هذه المقالة، نوضح ما هي الوظيفة المركبة (أو تكوين الوظائف). بالإضافة إلى ذلك، ستتمكن من رؤية عدة أمثلة للوظائف المركبة وكيفية حساب مجال هذا النوع من الوظائف. وأخيرًا، ستجد خصائص تكوين الوظيفة والعديد من التمارين خطوة بخطوة للتدرب عليها.

ما هو تكوين الوظيفة؟

يتكون تكوين الوظيفة من التقييم المتتابع لنفس قيمة المتغير المستقل (x) في وظيفتين أو أكثر. على سبيل المثال، تكوين الدوال (gof)(x) يعطي الدالة المركبة g[f(x)].

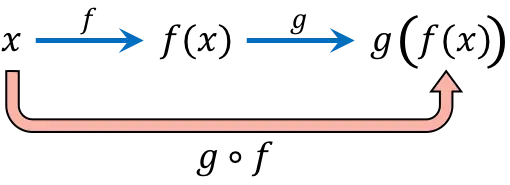
التعبير عن الوظيفة المركبة

$g\circ f$

نقرأ “f مكون من g” أو “f متبوعًا بـ g”.

لاحظ أن الترتيب مهم في تكوين الوظيفة، ويتم تطبيق الوظيفة الموجودة على يمين رمز التكوين أولاً

$(f)$

ثم الوظيفة الموجودة على يسار رمز التكوين

$(g).$

مثال على تكوين الوظيفة

نظرا لتعريف الدالة المركبة، دعونا نرى مثالا لكيفية حساب تكوين دالتين.

بالنظر إلى الوظيفتين المختلفتين التاليتين:

$f(x)=3x+1 \qquad g(x)=\cfrac{x+4}{2}$

احسب الدالة المركبة

$\left(g \circ f\right)(x)$

وتقييمه فيها

$x=3.$

تكوين الوظائف

$\left(g \circ f\right)(x)$

هذا يعني أننا بحاجة إلى أداء الوظيفة المركبة التالية:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

لحلها، نستبدل

$f(x)$

من خلال تعبيرها الجبري:

$g\Big(f(x)\Big)= g\Big(3x+1\Big)$

والآن نأخذ وظيفة

$g(x)=\cfrac{x+4}{2}$

ونضع التعبير

$3x+1$

حيث يوجد واحد

$x:$

$g\Big(3x+1\Big)=\cfrac{(3x+1)+4}{2}=\cfrac{3x+5}{2}$

بهذه الطريقة قمنا بالفعل بحساب الدالة f المكونة من g :

$\left(g \circ f\right)(x)=\cfrac{3x+5}{2}$

وأخيرا، لتقييم الدالة المركبة في

$x=3$

ما عليك سوى حساب صورة الوظيفة بالقيمة المذكورة:

$\left(g \circ f\right)(3)=\cfrac{3\cdot 3+5}{2}=\cfrac{14}{2}=7$

مجال الوظيفة المركبة

عادة، عندما نجري عمليات على الدوال، يكون مجال الدالة الناتجة هو تقاطع مجالات الدوال الأصلية. ومع ذلك، هذه الخاصية غير راضية عن تكوين الوظيفة.

مجال تكوين الوظيفة

$(g\circ f)(x)$

يعادل مجموعة جميع قيم x في مجال الدالة

$f$

مثل

$f(x)$

ينتمي إلى مجال الوظيفة

$g.$

$\text{Dom}(g\circ f)=\{x\in\text{Dom}(f)\ | \ f(x)\in \text{Dom}(g)\}$

لذلك، لحساب مجال دالة مركبة، يجب عليك أولاً العثور على مجال كل دالة على حدة، ثم مجال الدالة الناتجة عن العملية. وبالتالي فإن مجال تركيب الدوال سيتكون من جميع القيم التي تحقق الشرط الرياضي السابق.

👉 تذكر، إذا واجهت مشكلة ولا تعرف كيفية حلها، يمكنك سؤالنا في التعليقات أدناه!

خصائص تكوين الوظيفة

تتميز الوظائف المركبة بالخصائص التالية:

يحتوي تكوين الوظائف على الخاصية الترابطية، وبالتالي فإن المعادلة التالية صحيحة دائمًا:

$f\circ (g\circ h)=(f\circ g)\circ h$

بشكل عام، تكوين الدالة ليس تبادليًا، لذا فإن ترتيب العملية يحدد النتيجة:

$f\circ g\neq g\circ f$

يتوافق العنصر المحايد في تكوين الوظائف مع وظيفة الهوية
$f(x)=x.$

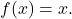
وبالتالي فإن أي دالة مكونة من دالة الهوية ينتج عنها الدالة نفسها:

$f\circ id = id \circ f = f$

$id = x$

إن حساب معكوس تركيب دالتين يعادل أولاً إيجاد معكوس كل دالة ثم تحديد الدالة المركبة:

$(f\circ g)^{-1}=f^{-1}\circ g^{-1}$

تعمل الدالة العكسية أيضًا كعنصر متماثل للدالة المركبة، حيث أن تكوين الدالة مع معكوسها يعادل دالة الهوية:

$(f\circ f^{-1})^{-1}=(f^{-1}\circ f)=id=x$

يتم حساب مشتق تكوين وظيفتين باستخدام قاعدة السلسلة:

$\bigl(g\circ f\bigr)'(x)=g'\Bigl(f(x)\Bigr)\cdot f'(x)$

➤ انظر: ما هي قاعدة السلسلة؟

تمارين محلولة على تكوين الوظائف

التمرين 1

نظرا للوظيفتين التاليتين:

$f(x)=x-2 \qquad g(x)= 5x + 4$

احسب تركيبات الدوال f المكونة من g و g المكونة من f .

$(g\circ f)(x)$

$(f\circ g)(x)$

انظر الحل

تكوين الوظائف

$\left(g \circ f\right)(x)$

يعني لحساب الوظيفة المركبة التالية:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

لذلك لحلها نستبدل

$f(x)$

للتعبير عنها:

$f(x)=x-2$

$g\Big(f(x)\Big)= g\Big(x-2\Big)$

$g\Big(x-2\Big)$

وهذا يعني أنه في التعبير

$g(x) =5x+4$

تحتاج إلى استبدال المتغير

$x$

$x-2:$

$g\Big(x-2\Big) = 5(x-2) +4= 5x-10+4 = 5x-6$

حتى الآن:

$\bm{\left(g \circ f\right)(x) = 5x-6}$

من ناحية أخرى، للعثور على الدالة g المكونة من f ، يجب عليك القيام بنفس الإجراء ولكن بالترتيب العكسي:

$\begin{aligned}\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&=f\Big(5x+4\Big)\\[2ex]&=(5x+4)-2\\[2ex]&=\bm{5x+2}\end{aligned}$

يوضح هذا التمرين أيضًا خاصية أن الوظائف المركبة ليست تبادلية، حيث أن النتيجة تعتمد على الترتيب الذي يتم به تطبيق الوظائف.

تمرين 2

نظرا للوظيفتين التاليتين:

$\displaystyle f(x) =x^2-3 \qquad g(x)=\frac{2x+3}{x+4}$

يحسب تكوين الوظائف f المكونة من g .

$(g\circ f)(x)$

انظر الحل

الدالة f المكونة من g تعني حل الوظيفة المركبة التالية:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

لذلك نستبدل الدالة f(x) بالتعبير الخاص بها:

$g\Big(f(x)\Big)= g\Big(x^2-3 \Big)$

والآن علينا أن نستبدل

$x$

$x^2-3$

في التعبير عن الدالة g(x):

$\begin{aligned}g\Big(x^2-3\Big)&=\cfrac{2(x^2-3)+3}{(x^2-3)+4}\\[2ex]&=\cfrac{2x^2-6+3}{x^2+1}\\[2ex]&=\cfrac{2x^2-3}{x^2+1}\end{aligned}$

وباختصار فإن نتيجة تكوين الوظيفة هي:

$\bm{\left(g \circ f\right)(x) =} \cfrac{\bm{2x^2-3}}{\bm{x^2+1}}$

التمرين 3

بالنظر إلى الدالتين التربيعيتين التاليتين:

$\displaystyle f(x) =x^2 \qquad g(x)=g(x)= x^2-4x+8$

تحديد نتيجة تكوين الوظائف التالية:

$(g\circ f)(2)$

انظر الحل

$\left(g \circ f\right)(2)$

يتكون من إيجاد الوظيفة المركبة التالية:

$\left(g \circ f\right)(2) = g\Big(f(2)\Big)$

إذن لحل الدالة المركبة، علينا حسابها أولًا

$f(2) :$

$f(x)=x^2$

$f(2)=2^2=4$

لذلك، كما

$f(2)=4 :$

$\left(g \circ f\right)(2) = g\Big(f(2)\Big) = g\big(4\big)$

لذا، للعثور على قيمة الدالة المركبة، عليك فقط الحساب

$g(4) :$

$\begin{aligned}\left(g \circ f\right)(2)&=g\Big(f(2)\Big)\\[2ex]&= g\big(4\big)\\[2ex]&=4^2-4\cdot 4+8 \\[2ex]&= 16 - 16 + 8\\[2ex]&= 8\end{aligned}$

وباختصار فإن نتيجة مشكلة تكوين الدالة هي:

$\bm{\left(g \circ f\right)(2) =8}$

التمرين 4

نظرا للوظيفتين التاليتين:

$\displaystyle f(x)=\frac{2x-2}{-x+7}\qquad g(x)= x^2-1$

أوجد نتيجة g المكونة من f عند x=2:

$(f\circ g)(2)$

انظر الحل

في هذه الحالة يجب علينا حساب الدالة المركبة التالية:

$\left(f \circ g\right)(2) = f\Big(g(2)\Big)$

لذلك نجد أولا

$g(2) :$

$g(x)=x^2-1$

$g(2)=2^2-1=4-1 = 3$

وهكذا مثل

$g(2)=3 :$

$\left(f \circ g\right)(2) = f\Big(g(2)\Big) = f\big(3\big)$

لذا، لحل الدالة المركبة، علينا حسابها

$f(3) :$

$\begin{aligned}\left(f \circ g\right)(2)&=f\Big(g(2)\Big)\\[2ex]&= f\big(3\big)\\[2ex]&=\cfrac{2\cdot 3-2}{-3+7}\\[2ex]&=\cfrac{6-2}{-3+7}\\[2ex]&=\cfrac{4}{4}\\[2ex]&=1\end{aligned}$