صيغة أويلر هي مفهوم رياضي يربط بين مفهومين أوليين في الرياضيات:الأعداد المركبة وعلم المثلثات. وهذا يجعلها واحدة من أهم المفاهيم وأكثر التطبيقات في جميع الرياضيات. سنرى خلال هذه المقالة كيف تبدو هذه الصيغة وجميع استخداماتها.
ما هي صيغة أويلر؟
صيغة أويلر هي معادلة رياضية أساسية تعتمد على رقم أويلر ، الذي يربط الأعداد المركبة بعلم المثلثات. اكتشفه عالم الرياضيات السويسري ليونارد أويلر في القرن الثامن عشر، ومنذ ذلك الحين تم استخدامه في مجموعة متنوعة من المجالات، من الفيزياء إلى علوم الكمبيوتر.
صيغة أويلر مكتوبة بالشكل e ix = cos(x) + i sin(x) ، حيث e هي أساس اللوغاريتم الطبيعي، i هي الوحدة التخيلية (تُعرف بالجذر التربيعي لـ -1)، وx هي قيمة حقيقية رقم. تحدد هذه المعادلة أن العدد المركب e ix يساوي مجموع العدد الحقيقي cos(x) وحاصل ضرب العدد التخيلي i بالرقم الحقيقي sin(x).

تكمن أهمية صيغة أويلر في أنها تسمح بالتعبير عن الأعداد المركبة من حيث الأعداد الحقيقية وعلم المثلثات، مما يسهل التعامل معها وحسابها.
إثبات صيغة أويلر
يعتمد إثبات صيغة أويلر على استخدام متسلسلة تايلور للدالة الأسية والهوية المثلثية لجيب التمام والجيب.
أولاً، نعتبر متسلسلة تايلور للدالة الأسية:

بعد ذلك، نستبدل x بـ ix في المعادلة أعلاه، حيث i هي الوحدة التخيلية (الجذر التربيعي لـ -1):
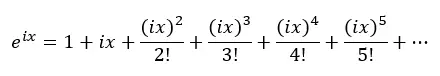
لذا نطبق قوى i ونعوض في المعادلة السابقة:
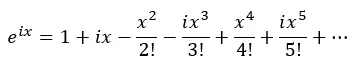
الآن نقوم بتجميع الحدود الحقيقية والشروط مع i:
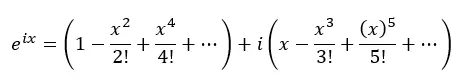
في الواقع، كل قوس من الأقواس أعلاه هو متسلسلة تايلور لجيب التمام والجيب:
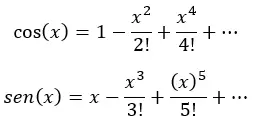
أخيرًا، نقوم بتبسيط (عن طريق استبدال كل تعبير بين قوسين بجيب التمام وجيب x) ونحصل على:

مثال على صيغة أويلر
الآن بعد أن عرفت كيفية عمل هذه الصيغة الرياضية، ننصحك بمحاولة حل المثال العملي التالي: التعبير عن العدد المركب e 2i (بالراديان) في صورة ذات الحدين:
التطبيق الرئيسي لصيغة أويلر هو تحويل العدد المركب المعبر عنه بالشكل الأسي إلى الشكل ذي الحدين. لذلك سوف نستخدم الصيغة : e ix = cos(x) + i sin(x)
ه 2i = جتا (2) + خطيئة (2)
e2i = -0.416 + 0.909i
وسيكون لدينا بالفعل العدد في صورة ذات الحدين. ومن هناك يمكننا أن نقوم بالتمثيل الرسومي في المستوى المعقد . للقيام بذلك، من الضروري أن نفهم أن الرقم المركب يتم تمثيله في المستوى المركب باستخدام الجزء الحقيقي على الإحداثيات (المحور السيني) والجزء التخيلي على الإحداثيات (المحور الصادي) كإحداثيات.
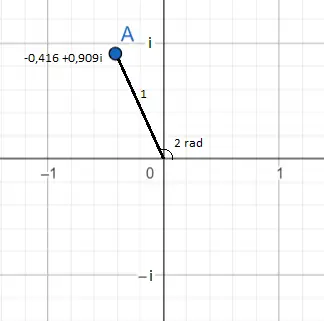
في الصورة السابقة يظهر الرقم المركب e 2i وهو يساوي -0.416 + 0.909i. يمكن رؤية ذلك كنقطة زرقاء اللون. ويمكن رؤية موقعه على الطائرة من زاويتين .
الأول والأكثر وضوحًا هو تمثيل الرقم في صيغة ذات الحدين : -0.416 (على الإحداثي الإحداثي) و0.909 (على الكمبيوتر). والثاني على الصورة الأسية : وحدة e 2i تساوي 1، لأنه الرقم الذي قبل e (بما أنه لا يوجد رقم قبل e، يجب أن نتخيل أنه يوجد 1) وفي الأس يوجد 2، وبالتالي فإن الوسيطة أو الزاوية تعادل اثنين راديان.
إذا لم تفهم هذه الفقرة الأخيرة تمامًا ، فنوصيك بقراءة مقالتنا عن الأعداد المركبة. حسنًا، سنقدم شرحًا متعمقًا للطرق المختلفة لكتابة العدد المركب وجميع خصائصه.
تمثيل رسومي لصيغة أويلر
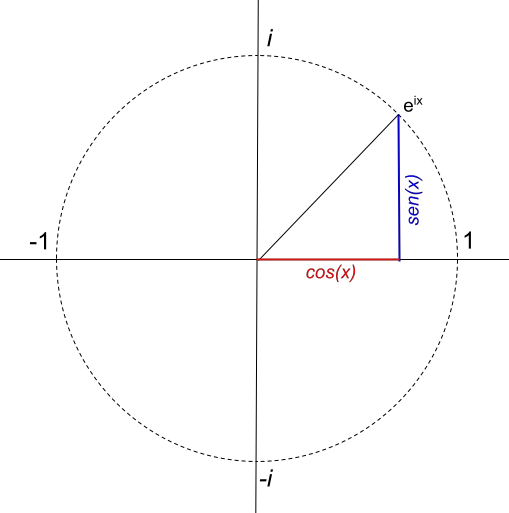
في المثال السابق، يمكنك أن ترى كيف يتم تطبيق صيغة أويلر وكيف يتم تمثيلها بيانيا في المستوى المركب. ولكن، إذا ذهبنا أبعد قليلاً وحاولنا تمثيل دالة مكافئة لصيغة أويلر، فسنجد شيئًا غريبًا للغاية: فهي تولد دائرة نصف قطرها 1 :
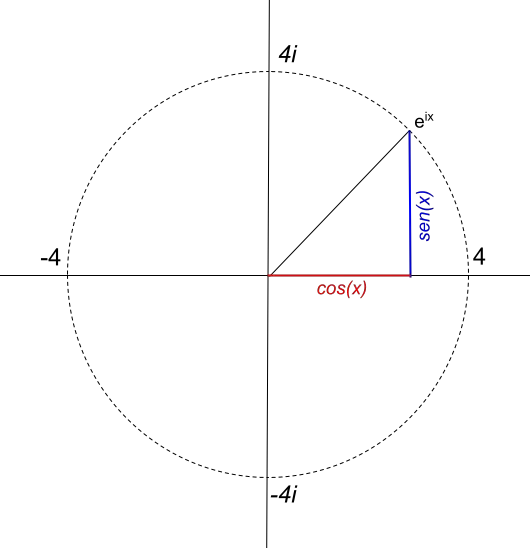
ومع ذلك، فإن نصف قطر الدائرة يعتمد بشكل مباشر على قيمة وحدة العدد المركب. على سبيل المثال، إذا أردنا تمثيل دائرة نصف قطرها 4، ستكون الدالة 4e ix . لذلك، يتم تمثيل الدالة 4e ix على النحو التالي:
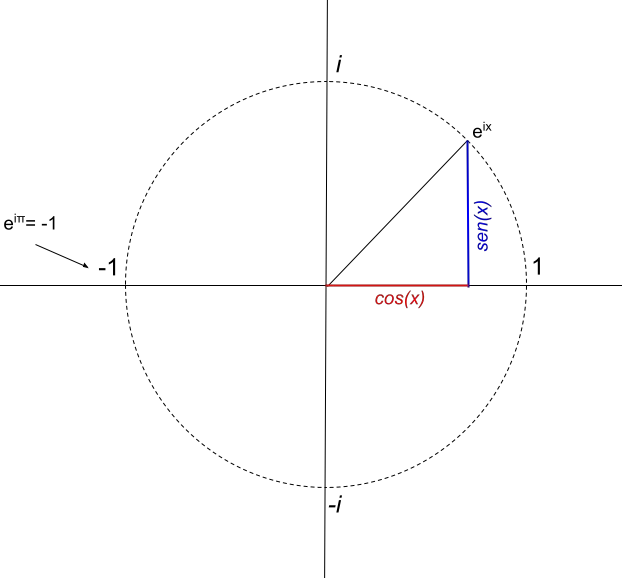
بالعودة إلى دائرة نصف القطر 1، إذا قررنا تمثيل e iπ (بالراديان)، فيجب علينا أولًا حساب:
ه πi = جتا (π) + أنا خطيئة (π)
eπi = -1 + i 0
eπi = -1
نحصل على e πi = -1، وهي هوية أويلر الشهيرة.
نستنتج من هذا أن العدد المركب e πi له جزء حقيقي واحد فقط، وهو يساوي -1. ولذلك فإن تمثيلها سيكون على النحو التالي:
تطبيقات صيغة أويلر
- الأعداد المركبة: صيغة أويلر هي العلاقة بين الدوال المثلثية والأعداد المركبة. من هذه الصيغة، يمكننا التعبير عن الأعداد المركبة بطرق مختلفة: ذات الحدين، والأسي، والقطبية.
- متسلسلة تايلور: تُستخدم صيغة أويلر لتوسيع دوال متسلسلة تايلور.
- الجبر الخطي: تُستخدم صيغة أويلر في قطر المصفوفة، وهي تقنية أساسية في الجبر الخطي.
- حساب التفاضل والتكامل: تستخدم صيغة أويلر في حل المعادلات التفاضلية، وهي تقنية ذات صلة في حساب التفاضل والتكامل.
بالإضافة إلى ذلك، فإن لها تطبيقات في العديد من النظريات الرياضية وحتى في مفاهيم خارج المجال الرياضي، مثل نظريات الفيزياء.
الاستنتاجات
كما رأيت في هذه المقالة، فإن أعظم تطبيق لصيغة أويلر هو في الأعداد المركبة : في تعبيرها العددي وفي تمثيلها. صحيح أن هذا له بعض التطبيقات في الجبر، لكنك تتعامل بشكل أساسي مع الأعداد المركبة. لذلك من المهم أن نفهمها جيدًا قبل كل شيء.
ومع ذلك، نأمل أن نكون قد ساعدناك على فهم هذا المفهوم بشكل أفضل. وإذا كان لديك أي أسئلة أو لا تعرف كيفية أداء التمرين، فلا تتردد في كتابتنا في التعليقات.