الرقم Pi هو ثابت رياضي يمثل العلاقة بين محيط الدائرة وقطرها. إنه رقم غير منطقي. وبعبارة أخرى، فإنه ليس جزءا دقيقا . ولذلك، لا يمكن تمثيله كرقم عشري منتهية. تبلغ قيمة Pi حوالي 3.14159 ويمثلها الحرف اليوناني π.
Pi هو رقم مهم في الرياضيات. ولذلك، فإن لها العديد من التطبيقات في مختلف المجالات. على سبيل المثال، يتم استخدامه في الهندسة لحساب المساحة. وكذلك محيط الدوائر والأشكال الدائرية الأخرى. ومن ناحية أخرى، في علم المثلثات لحساب الزوايا وأطوال الأقواس. وأخيرا، في الهندسة والفيزياء لحساب الكميات مثل الحجم والسعة.
يتم الاحتفال بيوم باي في 14 مارس من كل عام لأن التاريخ قريب من قيمة باي (3.14). يتم الاحتفال بهذا التاريخ لإحياء ذكرى دور باي في الرياضيات وتعزيز الاهتمام بهذا الثابت الأساسي.
من اكتشف الرقم Pi؟
الرقم Pi معروف منذ العصور القديمة، وكان عالم الرياضيات اليوناني أرخميدس (287-212 قبل الميلاد) هو من وصفه بدقة. في الواقع، استخدمه لحساب مساحة وحجم الأشكال الهندسية.
في القرن الثامن عشر، أثبت عالم الرياضيات السويسري يوهان لامبرت أن باي عدد غير نسبي . لاحقًا، في القرن التاسع عشر، أوضح عالم الرياضيات الألماني فرديناند فون ليندمان أن باي عدد متسامٍ . أي أنه لا يمكن التعبير عنها كحل دقيق لمعادلة متعددة الحدود ذات معاملات عقلانية.
على مر التاريخ، ساهم علماء الرياضيات المختلفون في فهم الرقم باي وطوروا تقنيات لحسابه بدقة أكبر. واليوم، تظل باي واحدة من أهم وأشهر الثوابت الرياضية في العالم ولا تزال موضوعًا للدراسة في الرياضيات.
لماذا الرقم Pi لانهائي؟
تبلغ قيمة Pi حوالي 3.14159، لكنه في الواقع رقم يستمر إلى ما لا نهاية بعد العلامة العشرية. هذا يعني أن Pi عدد لا نهائي ولا يمكن تمثيله بالكامل برقم عشري.
على الرغم من أن قيمة Pi لا نهائية، إلا أنه من الناحية العملية يمكن حساب القيم التقريبية لـ Pi بدقة كبيرة. حتى الآن، تم حساب ملايين أرقام Pi وتبين أنه لا يحتوي على أنماط منتظمة في أرقامه العشرية. على الرغم من أن هذا تم عن طريق أجهزة الكمبيوتر العملاقة لأننا لا نستطيع حساب هذا العدد الكبير من الأرقام.
ما هي الطرق الموجودة لحساب القيمة التقريبية للرقم Pi؟
هناك عدة طرق عملية لحساب قيمة Pi، وبعد ذلك سنشرح خطوة بخطوة الطرق الثلاث الأكثر استخدامًا من قبل علماء الرياضيات.
1. طريقة أرخميدس
استخدم عالم الرياضيات اليوناني أرخميدس طريقة هندسية لحساب القيمة التقريبية لـ Pi، لاستخدام هذه الطريقة اتبع الخطوات التالية:
1. ارسم دائرة وارسم خطاً يمر بمركز الدائرة ويتقاطع معه عند نقطتين متقابلتين كما هو موضح أدناه:
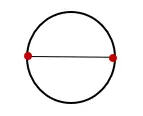
2. قم بقياس طول الخط الذي يتقاطع مع الدائرة وقم بتسميته “D”. وهذا القياس هو قطر الدائرة.
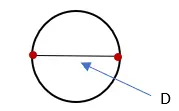
3. قم بقياس طول الخط الذي يشكل الدائرة وقم بتسميته “C”. وهذا القياس هو محيط الدائرة.
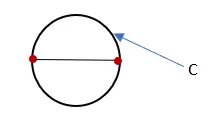
4. اقسم محيط الدائرة (ج) على قطر الدائرة (د). والنتيجة هي قيمة تقريبية لـ Pi.
على سبيل المثال: إذا كان قطر الدائرة 6 ومحيطها 18، فإن القيمة التقريبية لـ Pi هي 18 ÷ 6 = 3. من الواضح أن هذا المثال أساسي للغاية، ولكن إذا قمت بذلك بقيم محيط فعلي سترى أن الطريقة تعمل بشكل صحيح.
في الواقع، ننصحك بتجربتها: قم بقياس كوب أو أي شيء له شكل دائري ومعرفة ما إذا كان يناسبك.
2. طريقة مونت كارلو
طريقة مونت كارلو هي طريقة احتمالية تستخدم لحساب القيم التقريبية لـ Pi، وللقيام بذلك يتم إنشاء عدد كبير من النقاط بشكل عشوائي على المستوى ويتم حساب عدد النقاط التي تتناسب مع دائرة منقوشة في مربع. يتم تطبيق العملية على النحو التالي:
1. ارسم دائرة داخل مربع من ضلعه 1، كما هو موضح أدناه:

2. قم بتوليد عدد كبير من النقاط في المربع بشكل عشوائي.
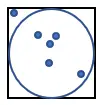
3. احسب عدد النقاط التي تناسب الدائرة. دعونا نسمي هذه الكمية “ن”.
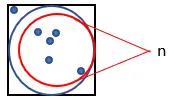
4. حساب إجمالي عدد النقاط التي تم إنشاؤها. نسمي هذه الكمية “م”.
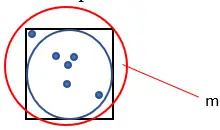
5. احسب القيمة التقريبية لـ Pi باستخدام الصيغة التالية: Pi = (4 · n) ÷ m.
على سبيل المثال، إذا تم إنشاء 380 نقطة وتم إدخال 300 نقطة في الدائرة، فإن القيمة التقريبية لـ Pi هي (4 · 300) ÷ 380 = 3.16. تشبه هذه القيمة إلى حد كبير أول منزلتين عشريتين لـ Pi، ولكن تمامًا مثل الطريقة السابقة، فإن استخدام القياسات الفعلية سيمنحك قيمة أكثر دقة .
3. طريقة التكرار
طريقة التكرار هي طريقة رياضية تستخدم لحساب القيم التقريبية لـ Pi. تستخدم هذه الطريقة صيغة تتضمن قيمة Pi ويتم تطبيقها بشكل متكرر لتحسين دقة الحساب. فيما يلي خطوات استخدام هذه الطريقة:
- اختر قيمة أولية لـ Pi. على سبيل المثال، يمكنك اختيار القيمة 3.
- استخدم صيغة تتضمن قيمة Pi لحساب قيمة تقريبية جديدة. على سبيل المثال، يمكنك استخدام الصيغة التالية: Pi = (Pi + (4 ÷ Pi)) ÷ 2
- قارن القيمة التقريبية الجديدة بالقيمة القديمة. إذا كان الفرق بين الاثنين صغيرا بما فيه الكفاية، فقد وصلت إلى نتيجة دقيقة. إذا كان الفرق لا يزال كبيرًا، فقم بتعيين القيمة الجديدة لـ Pi وكرر العملية من الخطوة 2.
على سبيل المثال، إذا كانت القيمة الأولية لـ Pi هي 3، فإن القيمة التقريبية الجديدة ستكون (3 + (4 ÷ 3)) ÷ 2 = 2.66666666. ولكن بما أن الفرق بين الاثنين ليس صغيرًا جدًا ، يمكنك دائمًا تكرار العملية عدة مرات قبل العثور على قيمة دقيقة.
ما هي تطبيقات الرقم Pi؟
باي هو رقم مهم في الرياضيات وله العديد من التطبيقات في مختلف المجالات. ومن أهم تطبيقات Pi لدينا ما يلي:
الهندسة
يُستخدم Pi في الهندسة لحساب مساحة ومحيط الدوائر والأشكال الدائرية الأخرى:
- الدوائر : احسب مساحة ومحيط الدوائر.
- المجالات : تحديد مساحة وحجم المجالات.
- الأسطوانات : حساب مساحة السطح وحجم الأسطوانات.
- المخاريط – تستخدم لحساب مساحة السطح وحجم المخاريط.
علم المثلثات
ومن المفيد في علم المثلثات لحساب الزوايا وأطوال القوس. بعض تطبيقاته هي:
- الزوايا : حساب الزوايا وأطوال القوس.
- الدوال المثلثية – تستخدم لحساب قيمة الدوال المثلثية لزوايا معينة.
- علم المثلثات الدائرية : لحساب قيم الدوال المثلثية للزوايا 360 درجة.
هندسة
في الهندسة، يتم استخدام Pi في حساب الكميات مثل الحجم والسعة. بعض تطبيقاته هي:
- الإلكترونيات : حساب الكميات مثل المقاومة والسعة.
- الكهرباء : تستخدم لحساب الكميات مثل القدرة والطاقة الكهربائية.
- الهندسة المدنية : حساب الكميات مثل مساحة السطح وحجم الهياكل وعناصر البناء.
بدني
الرقم Pi (π) هو ثابت رياضي له العديد من التطبيقات في الفيزياء. فيما يلي بعض الأمثلة على استخدام Pi في الفيزياء:
- الموجات – تستخدم لحساب التردد والطول الموجي للموجات.
- الميكانيكا : في الميكانيكا، يفيد في حساب الشغل والطاقة في الأنظمة الدوارة.
- الكهرومغناطيسية : في الكهرومغناطيسية، يمكن استخدامها لحساب الطاقة المخزنة في المكثف والتحريض في الملف.
- علم الكونيات في علم الكونيات، يتم استخدام Pi لحساب انحناء الزمكان وتوسع الكون.
ما هي التطبيقات التي يمتلكها الرقم Pi في الحياة الواقعية؟
فيما يلي بعض الأمثلة على كيفية استخدام Pi في الحياة اليومية:
- الهندسة : لتحديد مساحة حصيرة دائرية أو لقياس طول شريط القياس اللازم لتغطية محيط طاولة دائرية.
- الطبخ – تحديد كمية الماء أو السائل اللازمة لملء قدر أو عدد المكونات التي يمكن وضعها في وعاء دائري.
- علم الفلك : معرفة المسافة بين الكواكب والنجوم، ومدار الكواكب، ومواقع الأجرام السماوية في السماء.
- البستنة : معرفة كمية التربة أو التربة اللازمة لملء وعاء دائري أو لحساب كمية المياه اللازمة لسقي نبات في حديقة دائرية.