العمليات ذات الدوال: الجمع والطرح والحاصل والقسمة والتركيب

نوضح في هذه المقالة العمليات التي يمكن إجراؤها باستخدام الوظائف. ستتمكن من رؤية الشرح بالإضافة إلى التمارين المحلولة على العمليات باستخدام الدوال. وأخيرا، سوف تجد خصائص العمليات مع الوظائف.

ما هي العمليات مع الوظائف؟

يمكنك إجراء 5 أنواع مختلفة من العمليات باستخدام الوظائف: الجمع والطرح والضرب والقسمة والتركيب. أي أنه يمكن إضافة وظيفتين أو طرحهما أو ضربهما أو قسمتهما أو تركيبهما.

بعد ذلك، سنرى كيف يتم تنفيذ كل نوع من العمليات مع وظائف وخصائص كل منها.

مجموع الوظائف

قيمة مجموع (أو إضافة) وظيفتين تساوي مجموع قيمة كل وظيفة. بمعنى آخر، لحساب صورة دالة مجموعية، ما عليك سوى إضافة صور الدوال المشاركة في العملية.

$(f+g)(x)=f(x)+g(x)$

علاوة على ذلك، فإن مجال مجموع دالتين هو تقاطع مجال كل دالة مجمعة.

$\text{Dom}(f+g)=\text{Dom}(f)\cap\text{Dom}(g)$

دعونا نرى كيف تتم إضافة وظيفتين باستخدام مثال:

$f(x)=x^2+1 \qquad g(x)=\log(x-1)$

نضيف أولاً الوظيفتين:

$(f+g)(x)=f(x)+g(x)=x^2+1+\log(x-1)$

والآن نجد مجال دالة المجموع. للقيام بذلك، نحسب مجال كل دالة على حدة:

$\text{Dom}(f)=\mathbb{R}\qquad\text{Dom}(g)=(1,+\infty)$

➤ انظر: كيفية حساب مجال الدالة

فيكون مجال الدالة الناتجة عن العملية هو:

$\text{Dom}(f+g)=\text{Dom}(f)\cap\text{Dom}(g)=(1,+\infty)$

يجب أن تكون كل عملية ذات وظائف مصحوبة بمجالها الخاص لتحديد النتيجة بشكل كامل.

طرح الوظائف

صورة الطرح (أو الفرق) بين دالتين هي صور الطرح لكل دالة مشاركة في العملية:

$(f-g)(x)=f(x)-g(x)$

كما هو الحال مع دالة الجمع، فإن مجال الطرح لوظيفتين يعادل تقاطع مجال كل دالة.

$\text{Dom}(f-g)=\text{Dom}(f)\cap\text{Dom}(g)$

لذلك، إذا لم يتم تعريف الدالة عند قيمة معينة للمتغير المستقل x، فلن يتم تعريف الدالة الناتجة عن الطرح أيضًا.

دعونا نرى كيف يتم طرح وظيفتين من خلال مثال:

$f(x)=\sqrt{x}\qquad g(x)=\cfrac{3}{x-4}$

نطرح أولاً الوظيفتين:

$(f-g)(x)=f(x)-g(x)=\sqrt{x}-\cfrac{3}{x-4}$

ثم نحدد مجال دالة الطرح:

$\text{Dom}(f)=[0,+\infty)\qquad\text{Dom}(g)=\mathbb{R}-\{4\}$

$\text{Dom}(f-g)=\text{Dom}(f)\cap\text{Dom}(g)=[0,4)\cup (4,+\infty)$

المنتج الرئيسي

لحساب حاصل ضرب أو (ضرب) وظيفتين ، عليك ببساطة ضرب تعبيرات كل دالة.

$(f\cdot g)(x)=f(x)\cdot g(x)$

ومن ناحية أخرى، فإن مجال دالة المنتج هو مجموعة تقاطعات مجال كل دالة مضروبة.

$\text{Dom}(f\cdot g)=\text{Dom}(f)\cap\text{Dom}(g)$

على سبيل المثال، إذا كان لدينا الوظيفتين التاليتين:

$f(x)=\sqrt[3]{x^2-1}\qquad g(x)=\cfrac{2}{3x+6}$

أولاً نقوم بتشغيل المنتج بالوظيفتين التاليتين:

$(f\cdot g)(x)=f(x)\cdot g(x)=\sqrt[3]{x^2-1}\cdot\cfrac{2}{3x+6}=\cfrac{2\sqrt[3]{x^2-1}}{3x+6}$

وأخيرًا نجد مجال الدالة الناتجة عن العملية:

$\text{Dom}(f)=\mathbb{R}\qquad\text{Dom}(g)=\mathbb{R}-\{-2\}$

$\text{Dom}(f\cdot g)=\text{Dom}(f)\cap\text{Dom}(g)=(-\infty,-2)\cup (-2,+\infty)$

توزيع الوظائف

النتيجة العددية لتقسيم (أو حاصل) وظيفتين تتوافق مع المعادلة التالية:

$\displaystyle\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}$

ومع ذلك، فإن مجال تقسيم دالتين هو مجموعة تقاطعات مجال كل دالة ناقص كل x مما يلغي الدالة التي تعمل كمقسوم عليه، وإلا فإننا سنحصل على عدم التحديد.

$\displaystyle\text{Dom}\left(\frac{f}{g}\right)(x)=\text{Dom}(f)\cap\text{Dom}(g)-\{x:g(x)=0\}$

على سبيل المثال، سوف نقوم بتقسيم الوظائف التالية:

$f(x)=5^x \qquad g(x)=x-3$

توزيع الوظائف على النحو التالي:

$\displaystyle\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}=\cfrac{5^x}{x-3}$

ومن ناحية أخرى، فإن مجال كل دالة على حدة يتكون من جميع الأعداد الحقيقية

$\text{Dom}(f)=\mathbb{R}\qquad\text{Dom}(g)=\mathbb{R}$

ومع ذلك، بما أنه لا يمكن أن يكون هناك صفر في مقام الكسر، في مجال الدالة الناتجة، يجب علينا إزالة جميع القيم التي تلغي المقام (x=3).

$\displaystyle\text{Dom}\left(\frac{f}{g}\right)(x)=\text{Dom}(f)\cap\text{Dom}(g)-\{x:g(x)=0\}=\mathbb{R}-\{3\}$

تكوين الدوال

إن عملية تركيب الدوال هي العملية الأكثر صعوبة في حلها، لأنها المفهوم الأكثر تعقيدًا.

يتكون تكوين الوظيفة من التطبيق المتتالي لوظيفتين. جبريا، يتم التعبير عن تكوين وظيفتين على النحو التالي:

$(g\circ f)(x)=g\Bigl(f(x)\Bigr)$

ومن ناحية أخرى، مجال تكوين الوظائف

$(g\circ f)(x)$

يعادل مجموعة جميع قيم x في مجال الدالة

$f$

مثل

$f(x)$

ينتمي إلى مجال الوظيفة

$g.$

$\text{Dom}(g\circ f)=\{x\in\text{Dom}(f)\ | \ f(x)\in \text{Dom}(g)\}$

على سبيل المثال، بالنظر إلى الوظيفتين التاليتين:

$f(x)=x^2+1 \qquad g(x)=3x-4$

لإيجاد الدالة المركبة

$f$

تليها

$g$

نحن بحاجة إلى استبدال التعبير

$f(x)$

حيث يوجد واحد

$x$

في التعبير عن

$g(x):$

$\begin{aligned}(g\circ f)(x)&=g\Bigl(f(x)\Bigr)\\[2ex]&= g\Bigl(x^2+1\Bigr)\\[2ex]&=3(x^2+1)-4\\[2ex]&=3x^2+3-4\\[2ex]&=3x^2-1\end{aligned}$

في هذه الحالة، يتكون مجال الدالتين بالكامل من أرقام حقيقية، وبالتالي فإن مجال الدالة المركبة سيتكون أيضًا من أرقام حقيقية.

$\text{Dom}(g\circ f)=\mathbb{R}$

كما ترون، وظائف التأليف ليست عملية سهلة الفهم. لذلك ننصحك بممارسة تمارين تكوين الوظيفة التالية:

➤ انظر: تمارين محلولة على تركيب الوظائف

خصائص العمليات مع الوظائف

من بين جميع العمليات ذات الدوال، يتميز المجموع وحاصل الضرب بالخصائص التالية:

خاصية الترابط : الترتيب الذي تتم به إضافة أو ضرب 3 وظائف أو أكثر ليس له أي صلة.

$f(x)+\bigl[g(x)+h(x)\bigr]=\bigl[f(x)+g(x)\bigr]+h(x)$

$f(x)\cdot \bigl[g(x)\cdot h(x)\bigr]=\bigl[f(x)\cdot g(x)\bigr] \cdot h(x)$

الخاصية التبادلية : ترتيب جمع أو ضرب دالتين لا يغير النتيجة.

$f(x)+g(x)=g(x)+f(x)$

$f(x)\cdot g(x)=g(x)\cdot f(x)$

العنصر المحايد: عملية الجمع وعملية المنتج لهما وظائف عنصر محايد ثابتة
$f(x)=0$

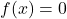
و

$f(x)=1$

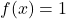
على التوالى.

العنصر المتماثل : دالة المجموع لها دالة معاكسة
$-f(x).$

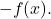
خاصية التوزيع : تربط هذه الخاصية مجموع العمليات وحاصل ضربها، وتقوم على المساواة التالية:

$f(x)\cdot \bigl[g(x)+h(x)\bigr]=f(x)\cdot g(x)+f(x)\cdot h(x)$