كيفية حساب نقاط القطع للدالة مع المحاور

تشرح هذه الصفحة ما هي نقاط تقاطع (أو تقاطع) الدالة مع المحاور الديكارتية وكيفية حسابها. بالإضافة إلى ذلك، ستجد العديد من الأمثلة لفهم كيفية العثور عليها بشكل كامل ويمكنك حتى التدرب على التمارين التي تم حلها خطوة بخطوة.

ما هي نقاط التقاطع (أو التقاطع) للدالة مع المحاور؟

قبل أن نرى كيفية حسابها، دعونا نتذكر ما هي نقاط تقاطع الدالة مع المحاور.

نقاط التقاطع أو تقاطع المحور هي النقاط التي يتقاطع فيها تمثيل الدالة مع محاور الإحداثيات، أي النقاط الموجودة على الرسم البياني التي ترتبط بالمحور X وعلى المحور l. المحور ص.

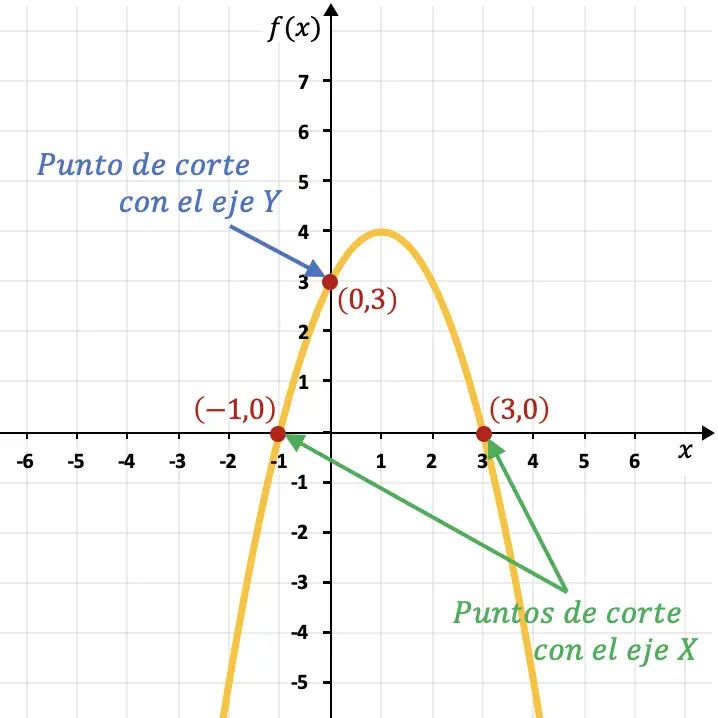
على سبيل المثال، القطع المكافئ في الرسم البياني التالي يتقاطع مع المحور Y عند النقطة (0,3) ويتقاطع مع المحور X عند النقطتين (-1,0) و(3,0).

نقطة القطع للدالة ذات المحور X

سيكون الإحداثي الثاني لنقاط تقاطع الدالة مع المحور X دائمًا 0، وبالتالي:

نقاط القطع لأي دالة للمحور السيني OX هي من الشكل

$(a,0)$

، ويمكن حسابها عن طريق حل المعادلة التالية:

$f(x)=0$

في بعض الأحيان عند حل هذه المعادلة يمكننا الحصول على حلين (أو أكثر)، وهذا يعني أن الدالة تتقاطع مع المحور X مرتين (أو أكثر). من ناحية أخرى، إذا لم يكن للمعادلة حل، فهذا يعني أن الدالة لا تتقاطع مع المحور X.

نقطة القطع للدالة ذات المحور Y

سيكون الإحداثي الأول لنقاط تقاطع الدالة مع المحور Y دائمًا 0، وبالتالي:

نقطة القطع لأي دالة ذات المحور y OY هي من الشكل

$(0,a)$

، ويمكن العثور عليها عن طريق حساب صورة الدالة عند x=0:

$f(0)$

على عكس نقاط التوقف على المحور X، يمكن أن تكون هناك نقطة توقف واحدة فقط على المحور Y.

مثال لحساب نقاط القطع للدالة ذات المحاور

وحتى لا يكون لديك أي شك، سنرى أدناه مثالاً لكيفية العثور على نقاط القطع لدالة ذات محاور ديكارتية:

أوجد عددياً نقاط القطع للدالة التالية:

$f(x)=-2x+4$

سنقوم أولاً بحساب نقطة القطع للدالة مع المحور السيني. نقطة التقاطع مع المحور X سيكون لها دائمًا المكون الثاني يساوي 0، أي أنها ستكون من النوع

$(a,0)$

. لأن f(x) يساوي دائمًا 0 على محور OX. إذن، لإيجاد المركبة الأخرى للنقطة، علينا حل المعادلة

$f(x)=0:$

$f(x)=0$

$-2x+4=0$

$-2x=-4$

$x=\cfrac{-4}{-2}=2$

وبالتالي فإن نقطة التقاطع مع المحور X هي:

$\bm{(2,0)}$

الآن سوف نجد نقطة التقاطع مع المحور y. نقطة التقاطع مع المحور Y سيكون لها دائمًا العنصر الأول يساوي 0، أي أن النقطة ستكون من النوع

$(0,a)$

. نظرًا لأن المتغير المستقل x يلغي دائمًا على المحور Y. إذن، لإيجاد الإحداثي الآخر للنقطة، علينا حسابه

$f(0):$

$f(0)=-2 \cdot 0+4=4$

وبالتالي فإن نقطة التقاطع مع المحور Y هي:

$\bm{(0,4)}$

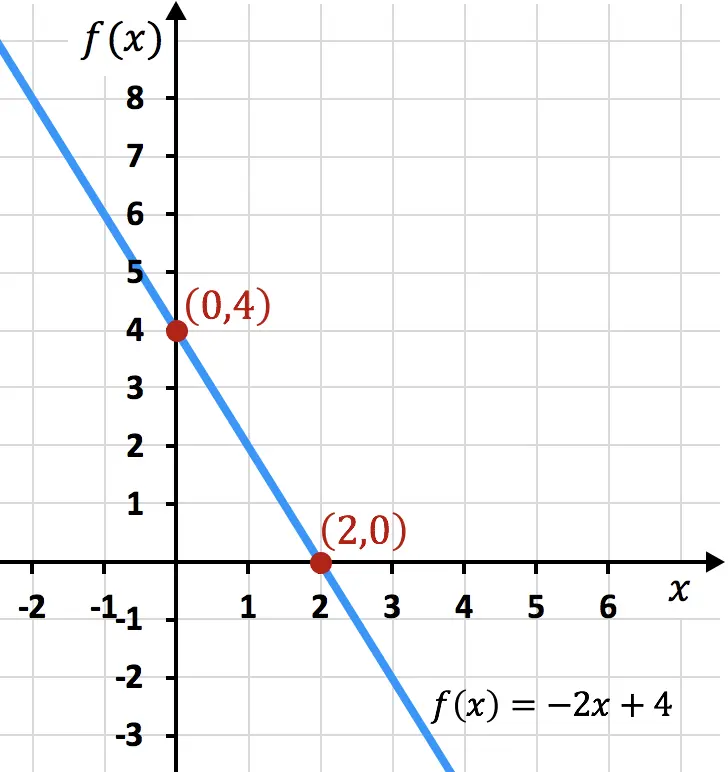
يوجد أدناه نموذج للدالة ممثلة بيانيًا، ويمكنك أن ترى أن الحدود الموجودة تتطابق مع تلك الموجودة في الرسم البياني:

كيفية العثور على نقاط القطع للدالة ذات المحاور

تمارين محلولة للنقاط المقطوعة للدالة ذات المحاور

التمرين 1

حدد نقاط القطع باستخدام المحاور الإحداثية للدالة التالية:

$f(x)=3x-3$

انظر الحل

نقطة القطع مع المحور X

للعثور على نقطة تقاطع الدالة مع المحور X من الضروري حلها

$f(x)=0:$

$f(x)=0$

$3x-3=0$

$3x=3$

$x=\cfrac{3}{3}=1$

وبالتالي فإن نقطة تقاطع الدالة مع المحور X هي:

$\bm{(1,0)}$

نقطة القطع مع المحور Y

للعثور على نقطة التقاطع مع المحور Y يجب عليك حساب

$f(0):$

$f(0)=3\cdot 0 -3= -3$

وبالتالي فإن نقطة تقاطع الدالة مع المحور Y هي:

$\bm{(0,-3)}$

تمرين 2

أوجد نقاط التقاطع مع المحاور الديكارتية للدالة التقريبية التالية:

$f(x)=2x+8$

انظر الحل

نقطة القطع مع المحور X

للعثور على نقطة نهاية الدالة مع محور OX، نحتاج إلى تعيين الدالة مساوية للصفر وحل المعادلة الناتجة:

$f(x)=0$

$2x+8=0$

$2x=-8$

$x=\cfrac{-8}{2}=-4$

وبالتالي فإن نقطة تقاطع الدالة مع محور الإحداثي السيني هي:

$\bm{(-4,0)}$

نقطة القطع مع المحور Y

للعثور على نقطة القطع مع محور OY، علينا الحساب

$f(0):$

$f(0)=2\cdot 0 +8= 8$

وبالتالي فإن نقطة تقاطع الدالة مع محور الكمبيوتر هي:

$\bm{(0,8)}$

التمرين 3

احسب نقاط القطع مع محاور الدالة التربيعية التالية:

$f(x)=x^2-3x+2$

انظر الحل

نقطة القطع مع المحور X

للعثور على نقطة تقاطع الدالة مع المحور X من الضروري حلها

$f(x)=0:$

$f(x)=0$

$x^2-3x+2=0$

في هذه الحالة، نحتاج إلى حل معادلة تربيعية، لذلك نطبق الصيغة:

$\displaystyle x =\cfrac{-b \pm \sqrt{b^2 -4ac}}{2a}$

$\displaystyle x=\cfrac{ -(-3) \pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2\cdot 1} = \cfrac{3 \pm 1}{2} = \begin{cases} 2 \\[2ex] 1 \end{cases}$

حصلنا على حلين للمعادلة التربيعية، بحيث تتقاطع الدالة مع المحور X عند نقطتين:

$\bm{(1,0)} \qquad \bm{(2,0)}$

نقطة القطع مع المحور Y

من ناحية أخرى، لتحديد نقطة التقاطع مع المحور Y، فمن الضروري حساب

$f(0):$

$f(0)=0^2-3\cdot 0+2= 2$

وبالتالي فإن نقطة تقاطع الدالة مع المحور Y هي:

$\bm{(0,2)}$

التمرين 4

أوجد نقاط التقاطع مع محاور المستوى الديكارتي للدالة النسبية التالية:

$f(x)=\cfrac{5}{x}$

انظر الحل

نقطة القطع مع المحور X

للعثور على نقطة تقاطع الدالة مع المحور X من الضروري حلها

$f(x)=0:$

$f(x)=0$

$\cfrac{5}{x}=0$

$5=0\cdot x$

$5=0$

$5\neq 0$

5 لا يعادل 0، وبالتالي فإن المعادلة ليس لها حل، وبالتالي لا توجد نقطة تقاطع بين الدالة والمحور X.

نقطة القطع مع المحور Y

للعثور على نقطة التقاطع مع المحور Y يجب عليك حساب

$f(0):$

$f(0)=\cfrac{5}{0}= \infty$

أي عدد مقسوم على صفر هو عدم تعيين ويعطي ما لا نهاية. لذلك، لا تمتد الدالة إلى ما بعد المحور Y عند أي نقطة.

باختصار، لا تحتوي دالة التمرين على نقاط تقاطع مع المحاور ، أي أن الرسم البياني الخاص بها لا يمر عبر المحور X أو المحور Y في أي نقطة.

التمرين 5

احسب نقاط القطع مع محاور دالة الدرجة الثالثة التالية:

$f(x)=x^3-9x$

انظر الحل

نقطة القطع مع المحور X

للعثور على نقطة تقاطع الدالة مع المحور X من الضروري حلها

$f(x)=0:$

$f(x)=0$

$x^3-9x=0$

يحتوي كلا حدي المعادلة على x ، والتي يمكننا من خلالها استخراج عامل مشترك:

$x(x^2-9)=0$

لكي تتحقق المساواة السابقة، يجب أن يكون أحد العوامل 0. لذلك، نجعل كل عامل يساوي الصفر للحصول على جميع الحلول الممكنة:

$\displaystyle x(x^2-9)=0 \ \longrightarrow \begin{cases} \bm{x = 0} \\[2ex] x^2-9 = 0\ \longrightarrow \ x^2=9 \ \longrightarrow \ \bm{x=\pm 3} \end{cases}$

وبذلك حصلنا على ثلاثة حلول لمعادلة الدرجة الثالثة، بحيث تقطع الدالة المحور X في 3 نقاط:

$\bm{(-3,0)} \qquad \bm{(0,0)} \qquad \bm{(3,0)}$

نقطة القطع مع المحور Y

لحساب نقطة القطع مع المحور Y، تحتاج إلى الحساب

$f(0):$

$f(0)=0^3-9\cdot 0 = 0$

ولذلك، فإن نقطة تقاطع الدالة الوحيدة مع المحور Y هي نقطة الأصل الإحداثية (0,0):

$\bm{(0,0)}$

لاحظ أننا سبق أن وجدنا هذه النقطة في حساب نقطة القطع مع المحور X، لأن الدالة تقطع عند هذه النقطة مع كلا المحورين في نفس الوقت.

نقاط القطع أو التقاطع للدالة مع المحاور

ما هي نقاط التقاطع (أو التقاطع) للدالة مع المحاور؟

نقطة القطع للدالة ذات المحور X

نقطة القطع للدالة ذات المحور Y

مثال لحساب نقاط القطع للدالة ذات المحاور

تمارين محلولة للنقاط المقطوعة للدالة ذات المحاور

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

اترك تعليقاً إلغاء الرد