النسب المثلثية للزاوية هي النسب التي يتم الحصول عليها من الجوانب الثلاثة للمثلث القائم. بمعنى آخر، هذه هي القيم التي تنتج من مقارنة أضلاعه الثلاثة باستخدام خارج القسمة (القسمة). على الرغم من أنه تجدر الإشارة إلى أن هذه الأسباب موجودة فقط في المثلثات القائمة (المثلثات التي لها زاوية 90 درجة).
النسب المثلثية في المثلث القائم
النسب المثلثية الستة الأكثر أهمية هي: جيب التمام، وجيب التمام، والظل، وقاطع التمام، والقاطع، وظل التمام. وبعد ذلك سنشرح بالتفصيل كيفية تعريف كل سبب من هذه الأسباب وسنتحدث عن الصيغة التي تميزها. ومن أجل فهم الشروحات التالية سنأخذ بعين الاعتبار المثلث القائم الزاوية التالي:

صدر
جيب الزاوية (الخطيئة أو الخطيئة) يساوي حاصل القسمة على الساق المقابلة (أ) بين الوتر (ج)، وبالتالي فإن صيغة الجيب هي: الخطيئة (α) = أ / ج . من المهم جدًا معرفة هذا التعريف للجيب، لأنه أساس كل علم المثلثات، إلى جانب الأسباب الأخرى التي سنغطيها في هذا القسم.
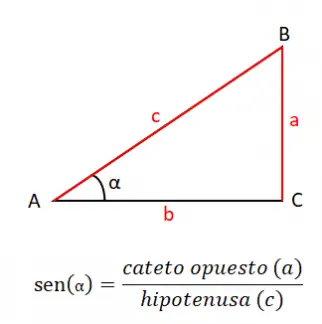
تراف من نظرية الجيب، يمكننا حساب أي جانب من المثلث ، يمكننا القيام بذلك عن طريق ربط خارج قسمة زاوية معينة بين الجانب المقابل لها. على سبيل المثال، إذا أردنا حساب الضلع أ ولدينا قيم الضلع بالزاويتين A و B، فيمكننا القيام بذلك باستخدام الصيغة: a / sin (A) = b / sin (B) . ومن خلال حل هذه المعادلة البسيطة، نحصل على القيمة المقابلة للمتغير الذي نريد حسابه.
جيب التمام
جيب تمام الزاوية (cos) يساوي حاصل القسم المجاور (b) بين الوتر (c)، وبالتالي فإن صيغة جيب التمام هي: cos (α) = b / c . في هذه الحالة، تتكون الصيغة من ضلعي المثلث المتصلين بالزاوية التي نريد دراستها، في هذا المثال الزاوية A أو α.
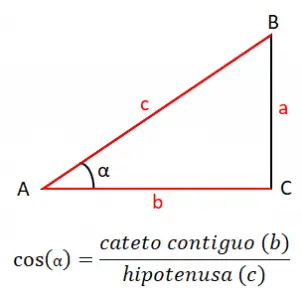
باستخدام جيب التمام، لدينا أيضًا طريقة لحساب أضلاع المثلث ، والتي تأتي من نظرية جيب التمام. يتيح لنا ذلك ربط الجوانب بالزوايا ويعطينا التعبيرات الثلاثة التالية:
أ² = ب² + ج² – 2ب جتا (أ)
ب² = أ² + ج² – 2أ ج كوس (ب)
ج² = أ² + ب² – 2أب كوس (ج)
الظل
السبب الثالث والأهم الذي سنغلق به مجموعة الأسباب الأصلية هو الظل (tan أو tg). يتم حساب ذلك بالقسمة بين الساق المقابلة (أ) والساق المجاورة (ب)، وبالتالي فإن صيغة الظل هي: tan (α) = a / b . يمكنك رؤيتها بيانيا أدناه:
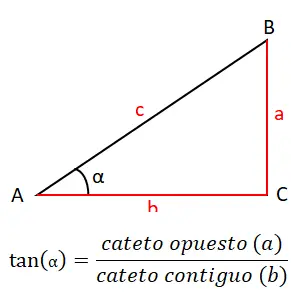
للظل أيضًا نظرية خاصة به، تسمى نظرية الظل. وهذا يسمح لنا بربط طولي ضلعي المثلث مع مماسات الزوايا . وجاء البيان كما يلي: “”حاصل مجموع الضلعين المحصورين بين طرحهما يساوي خارج القسمة بين ظل متوسط الزاويتين المقابلتين لهذين الضلعين، وظل نصف الفرق بينهما””.
النسب المثلثية المشتقة
من النسب المثلثية الثلاث التي ناقشناها للتو، يمكننا الحصول على نسب مثلثية مشتقة أخرى. يتم الحصول عليها عن طريق أخذ النسبة العكسية فيما يتعلق بجيب التمام وجيب التمام والظل.
- قاطع التمام: هي النسبة العكسية للجيب ويتم حسابها بالصيغتين: cosec (α) = c / a وcosec (α) = 1 / sin (α).
- القاطع: هو النسبة العكسية لجيب التمام ويتم حسابه بالصيغتين: sec (α) = c / b و sec (α) = 1 / cos (α).
- ظل التمام: هو النسبة العكسية للظل ويتم حسابه بالصيغتين: cotg (α) = b / a و cotg (α) = 1 / tan (α).
جدول النسب المثلثية
أدناه يمكنك رؤية جدول يلخص جميع الأسباب الموضحة حتى الآن. باستخدام هذا الجدول، ستتمكن من حفظ جميع الصيغ بفعالية، لأنه يتيح لك التمييز بسهولة بين الاختلافات بين كل تعبير رياضي.
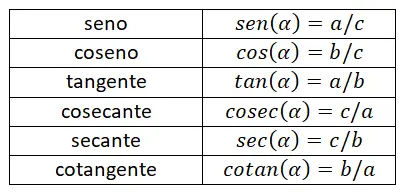
النسب المثلثية في الدائرة
هناك طريقة أخرى لدراسة علم المثلثات وهي من خلال محيط المثلثات أو دائرة الوحدة ، وهذا المحيط له نصف قطر يساوي 1 وأصله هو النقطة (0، 0). يتكون الرسم من دائرة ومثلث قائم الزاوية مصورين داخل الدائرة، وبشكل أدق يجب أن تلامس الزاوية التي سندرسها النقطة الأصلية.
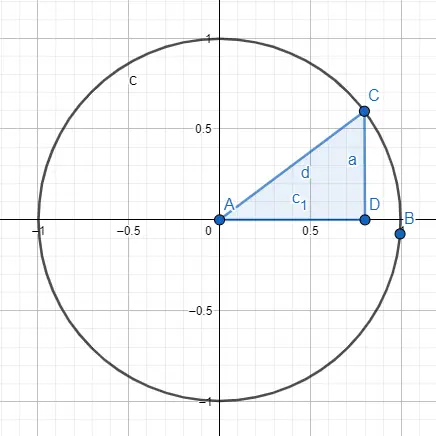
عندما تكون لدينا هذه الصورة، نعلم أن نصف القطر يساوي الوتر، وهو ما يساوي 1. لذلك إذا أردنا حساب الجيب وجيب التمام، فسنستخدم قيمة نصف القطر وقيمة الجوانب الأخرى للضلع المثلث. لحساب الجيب، سنقوم بالحساب التالي: sin (A) = CD / AC = CD / radius = CD / 1 = CD ، وبالتالي فإن جيب A هو a. من ناحية أخرى، لحساب جيب التمام، سنقوم بالحساب: cos (A) = AD / AC = AD / radius = AD / 1 = AD ، وبالتالي فإن جيب تمام A هو c1.
من المهم جدًا أن تضع شيئين في الاعتبار. الأول أن استخدام هذه الدائرة في دراسة النسب المثلثية يرجع إلى ضرورة التعامل مع زوايا أكبر من تلك التي يمكن دراستها بالمثلث. على سبيل المثال، لا يمكن دراسة الزاوية التي قياسها 150 درجة من خلال مثلث بسيط، لأنها كبيرة جدًا. والشيء الثاني الذي يجب أخذه في الاعتبار هو أن جيب الجيب وجيب التمام لا يمكنهما أبدًا اعتماد قيم أكبر من 1 وأقل من -1.
علامة النسب المثلثية
كما قلنا من قبل، للتعامل مع الزوايا الأكبر من المثلث الذي يسمح لنا بالتعامل معه، نستخدم محيط الزوايا. للقيام بذلك قمنا بتمثيل مثلث داخل الدائرة بالضبط في أحد الأرباع الأربعة التي تقسم المحيط، في الصورة التالية يمكنك رؤية الأرباع الأربعة ممثلة.
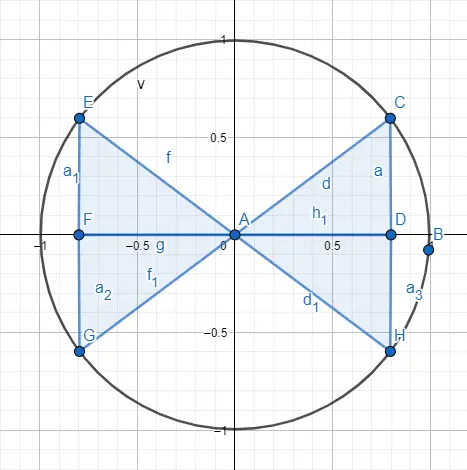
لذا، يجب التمييز بين الزاوية التي قياسها 30 والزاوية التي قياسها 210، والتي تصبح واحدة بخصوص التوزيع داخل المثلث ، سنستخدم توزيع العلامات حسب الربع الذي يقع فيه المثلث. أدناه يمكنك رؤية العلامات المقابلة لكل ربع ومثال مرسوم.
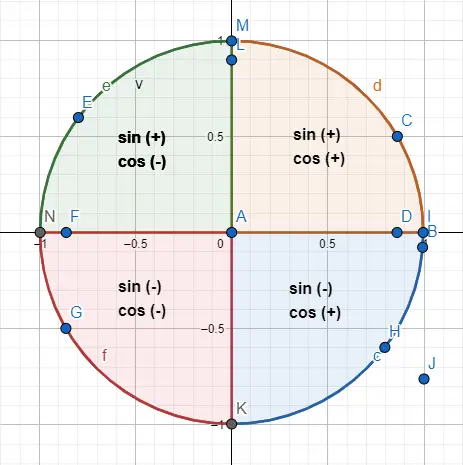
على سبيل المثال، الزاويتان 30 درجة و210 درجة تشتركان في نفس القيمة العددية ، لكن جيب التمام وجيب التمام لهما إشارات معاكسة. إذن: sin(30) = 1/2 وcos(30) = √3/2، بينما sin(210) = -1/2 وcos(210) = -√3/2. وللحصول على هذه النتيجة قمنا بتمثيل الزاويتين على المحيط (الصورة أدناه) واتبعنا مؤشرات العلامات.
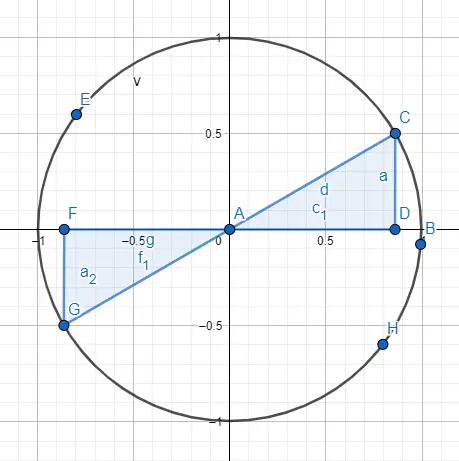
أخيرًا، كيف يمكن أن يكون لديك زوايا أكبر من 360 درجة ، على الرغم من أن الأمر قد لا يبدو كذلك لأن المحيط 360 درجة فقط. لكن، إذا أردنا إيجاد زاوية قياسها 750 درجة، فيمكننا تقليلها إلى زاوية تتراوح بين 0 درجة و360 درجة. ببساطة نقسم 750 على 360 والباقي هو الزاوية المتبقية، في حالة 750 درجة نحصل على زاوية 30 درجة.
أنواع الزوايا حسب الربع
توجد علاقات بين زوايا مختلفة، مما يسمح لنا بحساب النسب القيم المثلثية لجميع الزوايا التابعة للدائرة. دعونا نحصل على هذه الأسباب من التخفيض إلى الربع الأول . وهذا يعني أننا نقوم بالتبسيط من زاوية معينة إلى الربع الأول ثم نطبق العلامات المقابلة لها. ستجد أدناه شرحًا للإجراءات المختلفة (حسب الربع):
الربع الأول
في هذا الربع الأول (0 درجة – 90 درجة)، علينا فقط حل النسبة المثلثية بالزاوية المعطاة لنا. وإذا نظرنا إلى الصورة التي شرحناها سابقًا عن الرموز، فإن الجيب وجيب التمام أمامهما موجب (النتيجة التي نحصل عليها لن تتأثر بالعلامة).
التخفيض من الربع الثاني إلى الأول
في الربع الثاني (90 درجة – 180 درجة) نتعامل مع زوايا متكاملة، مما يعني أن مجموع الزاويتين يساوي 180 درجة. لذلك، نحن بحاجة إلى إجراء تصغير من الربع الثاني إلى الأول ونفعل ذلك بالصيغة 180 – α = β ، حيث α هي زاوية الربع الأول و β هي الزاوية الأصلية.
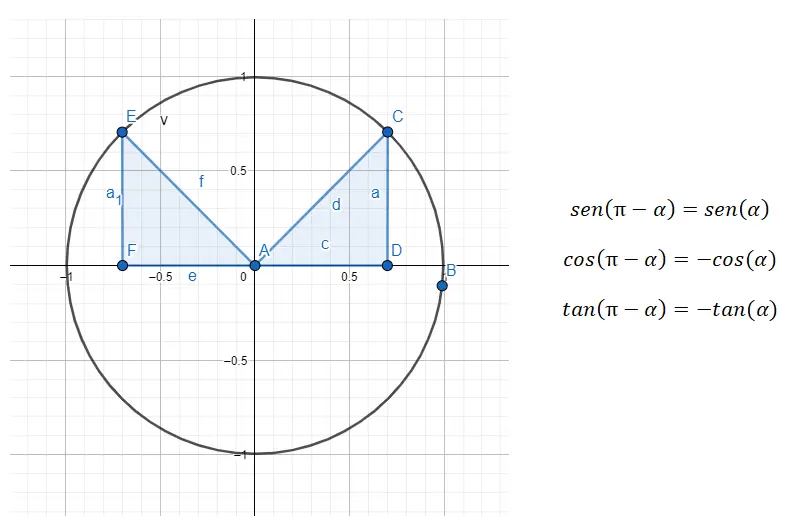
على سبيل المثال، إذا حصلنا على الزاوية 135 درجة (التي تنتمي إلى الربع الثاني)، فعلينا إيجاد الزاوية من الربع الأول المرتبطة بهذه الزاوية أولاً. في هذا المثال، الزاوية (α) التي نبحث عنها هي 45 درجة، حيث أن 180 – 45 = 135. لذا، سيكون هذا صحيحًا: sin (135) = sin (180 – 45) = sin (45)، cos (135) ) = cos (180 – 45) = -cos (45) وtan (135) = tan (180 – 45) = -tan (45).
تخفيض الربع الثالث إلى الأول
في الربع الثالث (180 درجة – 270 درجة) ، نحن نتعامل مع زوايا تختلف بمقدار 80 درجة، مما يعني أن الزوايا متباعدة بمقدار 180 درجة. لذا، إذا أردنا التبسيط من الربع الثالث إلى الأول، فعلينا استخدام الصيغة 180 + α = β ، حيث α هي زاوية الربع الأول و β هي الزاوية الأصلية.
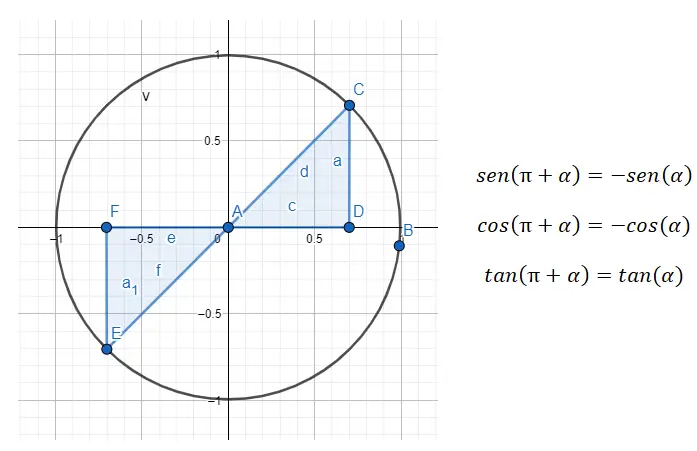
على سبيل المثال، إذا أعطيت لنا الزاوية 225 درجة (التي تنتمي إلى الربع الثالث)، فعلينا إيجاد زاوية الربع الأول التي تتوافق معها. في حالة 225 درجة، الزاوية (α) التي نبحث عنها هي مرة أخرى 45 درجة، حيث أن 180 + 45 = 225. لذا، sin (225) = sin (180 + 45) = -sin (45)، cos (225) = cos (180 + 45) = -cos (45) وtan (225) = tan (180 + 45) = tan (45) سيكونان مكتملين. ).
تخفيض الربع الرابع إلى الأول
في الربع الرابع (270 درجة – 360 درجة) نتعامل مع زاويتين متقابلتين، مما يعني أن الزوايا متساوية عددياً، لكن لها إشارات متضادة , مثل 30° و-30° (أي ما يعادل 330°، حيث أن 360° – 30° = 330°) . من المهم أن تضع في اعتبارك أنه يمكن كتابة الزوايا المتقابلة كزاوية موجبة وزاوية سالبة أو كزاويتين موجبتين (في المثال الذي ناقشناه للتو، شرحنا الفرق).
لذا، إذا أردنا إجراء تصغير من الربع الرابع إلى الأول، فسنحتاج إلى استخدام الصيغة 360 – α = β ، حيث α هي زاوية الربع الأول و β هي الزاوية الأصلية.
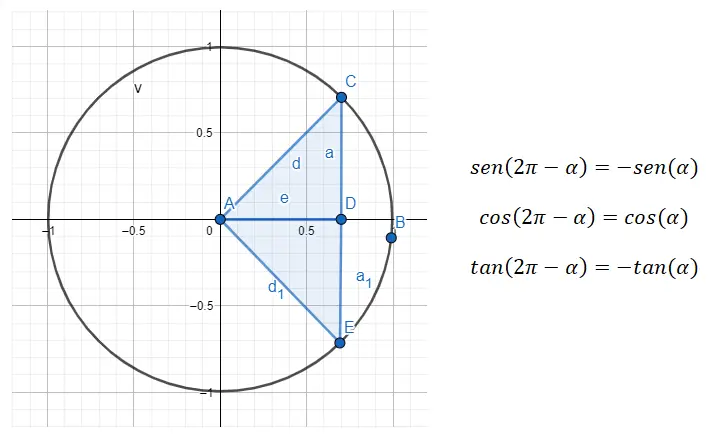
على سبيل المثال، إذا حصلنا على الزاوية 315 درجة (التي تنتمي إلى الربع الرابع)، فعلينا إيجاد زاوية الربع الأول المرتبطة بهذه الزاوية أولاً. في حالة الزاوية (α) التي نبحث عنها، فهي لا تزال 45 درجة، حيث أن 360 – 45 = 315. وبالتالي، sin (315) = sin (360 – 45) = -sin (45)، cos ( 315) ) = cos (360 – 45) = cos (45) وtan (315) = tan (360 – 45) = -tan (45). في الختام، لقد رأينا الزوايا المشتقة من 45 درجة لجميع الأرباع.
النسب المثلثية لأهم الزوايا
هناك عدد من الزوايا، تسمى الزوايا البارزة ، وهي الأكثر شيوعًا في علم المثلثات. يوصى بشدة بمعرفة النسب المثلثية عن ظهر قلب. ولذلك قمنا أدناه بإنشاء جدول يحتوي على النسب المثلثية لهذه الزوايا ومشتقاتها (نفس الزوايا ولكن بفارق 90 أو 180 أو 270 درجة):
| الزاوية (°) | الزاوية (راد) | صدر | جيب التمام | الظل |
| 0 درجة | 0 راد | 0 | 1 | 0 |
| 30 درجة | 1/6 راد | 1/2 | √3/2 | √3/3 |
| 45 درجة | 1/4 راد | √2/2 | √2/2 | 1 |
| 60 درجة | 1/3 راد | √3/2 | 1/2 | √3 |
| 90 درجة | 1/2πراد | 1 | 0 | ∞ |
| 120 درجة | 5/8πراد | √3/2 | -1/2 | -√3 |
| 135 درجة | 3/4 راد | √2/2 | -√2/2 | -1 |
| 150 درجة | 5/8πراد | 1/2 | -√3/2 | -√3/3 |
| 180 درجة | πراد | 0 | -1 | 0 |
| 225 درجة | 5/4 راد | -√2/2 | -√2/2 | 1 |
| 270 درجة | 3/2 ط راد | -1 | 0 | ∞ |
| 315 درجة | 7/4 ط راد | -√2/2 | √2/2 | -1 |
العلاقة بين النسب المثلثية
هناك عدة طرق للربط بين النسب المثلثية المختلفة. ومن هذه العلاقات نحصل على نوع من التساوي بين الدوال المثلثية المختلفة، وهو ما نسميه المتطابقات المثلثية. بفضل هذا النوع من الهويات يمكننا حساب النسبة بناءً على أي نسبة أخرى. تجدر الإشارة إلى أن هناك العديد من أنواع المتطابقات المثلثية المختلفة، والتي يتم تصنيفها بناءً على نوع العلاقة التي تدعم التعبير نفسه.
النسب المثلثية حل المشاكل
بعد ذلك، نقدم لك سلسلة من التمارين التي يمكنك من خلالها تطبيق جميع النظريات الموضحة في هذه المقالة. تذكر أنه إذا كنت عالقًا أو كانت لديك أسئلة في أي وقت، فيمكنك إعادة قراءة المقالة وبالتأكيد، من خلال القراءة الثانية ، ستفهم كل شيء بشكل أفضل. ومع ذلك، يمكنك البدء في ممارسة:
التمرين 1
احسب النسب المثلثية الست للزاوية 225 درجة:
سنبدأ بحساب الزاوية (α) التي تساوي: 180 + α = 225°، وبالتالي α = 45°.
خطيئة(225) = خطيئة(180 + 45) = -خطيئة(45) = -√2/2
cos(225) = cos(180 + 45) = -cos(45) = -√2/2
ظا(225) = ظا(180 + 45) = ظا(45) = 1
تمرين 2
احسب النسب المثلثية الستة للزاوية 120 درجة:
سنبدأ بحساب الزاوية (α) التي تساوي: 180 – α = 120°، وبالتالي α = 60°.
خطيئة(120) = خطيئة(180 – 60) = خطيئة(60) = √3/2
cos(120) = cos(180 – 60) = -cos(60) = -1/2
ظا(120) = ظا(180 – 60) = – ظا(60) = -√3
التمرين 3
احسب النسب المثلثية الست للزاوية 510°:
قبل البدء، يجب عليك إجراء تصغير الزاوية: 510 / 360 = دورة واحدة وزاوية 150 متبقية. بعد ذلك، نحسب الزاوية (α) التي تساوي: 180 – α = 150، وبالتالي α = 30°.
الخطيئة (150) = الخطيئة (180 – 30) = الخطيئة (30) = 1/2
cos(150) = cos(180 – 30) = -cos(30) = -√3/2
ظا(150) = ظا(180 – 30) = – ظا(30) = -√3/3