الدوال الأسية: الخصائص، التمثيل البياني، التمارين،...

في هذه الصفحة سوف تكتشف ما هي الدوال الأسية وكذلك كيفية تمثيل الدالة الأسية على الرسم البياني. بالإضافة إلى ذلك، سترى جميع خصائصه والعديد من الأمثلة لفهمه بالكامل. وأخيرًا، سوف تكون قادرًا على التدرب على التمارين والمسائل التي تم حلها خطوة بخطوة على الدوال الأسية.

ما هي الدالة الأسية؟

تعريف الدالة الأسية هو كما يلي:

في الرياضيات، الدوال الأسية هي دوال لها المتغير المستقل x في أس القوة. وبعبارة أخرى فهي كما يلي:

$f(x)=a^x$

ذهب

$a$

هو عدد حقيقي موجب ويختلف عن 1.

أمثلة على الوظائف الأسية

الوظائف التالية هي أمثلة على الوظائف الأسية:

$f(x)=3^{x}$

$f(x)=4^{-x}$

$\displaystyle f(x)=\left( \frac{1}{2} \right)^x$

$f(x)=5^x$

خصائص الدوال الأسية

الدوال الأسية لها الخصائص التالية:

مجال الدالة الأسية يتكون من أرقام حقيقية، أو بمعنى آخر، توجد دالة أسية لأي قيمة لـ x .

$\text{Dom } f=\mathbff{R}$

ومع ذلك، فإن الدالة تأخذ قيمًا موجبة فقط، وبالتالي فإن نطاق الدالة الأسية يتكون من أرقام حقيقية موجبة.

$\text{Im } f= (0,+\infty)$

كل دالة أسية هي دالة مستمرة وحقنية.

إذا لم تتم ترجمة الدالة، فإن أي دالة أسية تمر عبر النقطة (0،1). لأن الدالة التي قيمتها صفر تعطي دائمًا واحدًا.

$f(0)=a^0=1$

وبالمثل، فإن قيمة الدالة الأسية عند x=1 تساوي الأساس.

$f(1)=a^1=a$

إذا كانت قاعدة السلطة
$(a)$

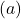
أكبر من 1، الدالة الأسية آخذة في التزايد. ومن ناحية أخرى، إذا كان المعامل

$a$

في الفترة بين 0 و 1، فإن الدالة الأسية آخذة في التناقص.

بشكل عام، المحور السيني هو خط مقارب أفقي للدالة الأسية.

معكوس الدالة الأسية هو الدالة اللوغاريتمية. ولذلك، فإن الرسوم البيانية للدالة الأسية والدالة اللوغاريتمية تكون متناظرة حول الخط y=x إذا كان كلاهما لهما نفس الأساس.

كيفية رسم دالة أسية

من السهل جدًا تمثيل الوظائف الأسية. لذلك دعونا نرى كيفية رسم دالة أسية على الرسم البياني باستخدام مثال.

ارسم الدالة الأسية التالية على الرسم البياني:

$f(x)=2^x$

في الدوال الأسية، ليست هناك حاجة لحساب المجال، لأنها ستكون دائمًا أرقامًا حقيقية:

$\text{Dom } f = \mathbb{R}$

لذلك يكفي إعداد جدول القيم. وبما أن هذه الأنواع من الوظائف تتغير كثيرًا من نقطة إلى أخرى، فسوف نقوم بحساب 5 نقاط. لكن كلما زاد عدد النقاط التي نحسبها، أصبح تمثيل الدالة أكثر دقة.

$x= 0 \ \longrightarrow \ f(0)=2^0= 1$

$x= 1 \ \longrightarrow \ f(1)=2^1= 2$

$x= 2 \ \longrightarrow \ f(2)=2^2= 4$

$x= -1 \ \longrightarrow \ f(-1)=2^{-1}= 0,5$

$x= -2 \ \longrightarrow \ f(-2)=2^{-2}= 0,25$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 4 \\ -1 & 0,5 \\ -2 & 0,25 \end{array}$

ننصح باستخدام الآلة الحاسبة للعثور على النقاط في جدول القيم، نظرًا لصعوبة حسابها يدويًا.

الآن نمثل النقاط على الرسم البياني :

وأخيرًا، نقوم بربط النقاط وتوسيع الدالة:

لاحظ أن الدالة الموجودة على اليمين تستمر في النمو حتى ما لا نهاية.

في المقابل، الدالة الموجودة على اليسار تتناقص ولكنها لا تصل أبدًا إلى 0. وعلى الرغم من أنها تقترب منها كثيرًا، إلا أنها لا تلمسها أبدًا. هذا يعني أن الخط y=0 (المحور x) هو خط مقارب أفقي.

تمارين محلولة على الدوال الأسية

التمرين 1

ارسم الدالة الأسية التالية:

$f(x)= 2^x+1$

انظر الحل

إنها دالة أسية، لذا لتمثيلها يجب عليك إنشاء جدول قيم يعطي قيم للمتغير x:

$x= 0 \ \longrightarrow \ f(0)= 2^0+1=2$

$x= 1 \ \longrightarrow \ f(1)= 2^1+1=3$

$x= 2 \ \longrightarrow \ f(2)= 2^2+1=5$

$x= -1 \ \longrightarrow \ f(-1)= 2^{-1}+1=1,5$

$x= -2 \ \longrightarrow \ f(-2)= 2^{-2}+1=1,25$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 3 \\ 2 & 5 \\ -1 & 1,5 \\ -2 & 1,25 \end{array}$

بمجرد حصولنا على جدول القيم، نرسم النقاط التي تم الحصول عليها على الرسم البياني ونرسم الدالة:

لاحظ أن الدالة الموجودة على اليمين تستمر في النمو حتى ما لا نهاية. من ناحية أخرى، على اليسار، تقل الدالة ولكنها لا تتجاوز 1 أبدًا. في الواقع، الدالة لها خط تقارب أفقي على اليمين y=1.

في هذه الحالة، يكون الخط المقارب الأفقي عند y=1 بدلاً من المحور OX لأنه تم إجراء ترجمة رأسية لوحدة واحدة لأعلى باتجاه الدالة.

تمرين 2

ارسم الدالة الأسية التالية على الرسم البياني:

$\displaystyle f(x)= \left(\frac{1}{3}\right)^x$

انظر الحل

إنها دالة أسية، لذا لتمثيلها بيانياً يجب إنشاء جدول قيم يعطي قيماً للمتغير x:

$x= 0 \ \longrightarrow \ f(0)= \left(\cfrac{1}{3}\right)^0 = 1$

$x= 1 \ \longrightarrow \ f(1)= \left(\cfrac{1}{3}\right)^1 = 0,33$

$x= 2 \ \longrightarrow \ f(2)= \left(\cfrac{1}{3}\right)^2 = 0,11$

$x= -1 \ \longrightarrow \ f(-1)= \left(\cfrac{1}{3}\right)^{-1} = 3$

$x= -2 \ \longrightarrow \ f(-2)= \left(\cfrac{1}{3}\right)^{-2} = 9$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 0,33 \\ 2 & 0,11 \\ -1 & 3 \\ -2 & 9 \end{array}$

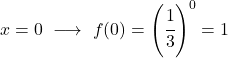
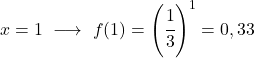
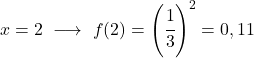
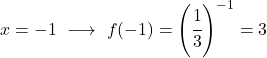
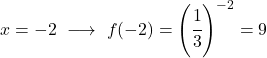
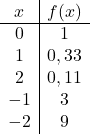
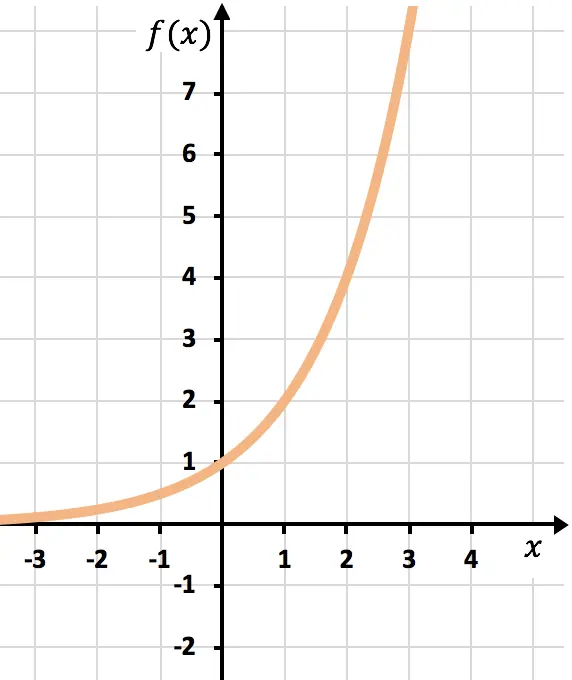
بمجرد حصولنا على جدول القيم، نرسم النقاط المحسوبة على الرسم البياني ونرسم الدالة:

لاحظ أن الدالة الموجودة على اليسار تستمر في النمو حتى ما لا نهاية. من ناحية أخرى، على اليمين، تقل الدالة ولكنها لا تتجاوز 0 أبدًا. في الواقع، الدالة لها خط تقارب أفقي عند y=0 (المحور X).

التمرين 3

ارسم الدالة الأسية التالية على الرسم البياني:

$\displaystyle f(x)= \left(\frac{1}{2}\right)^x+3$

انظر الحل

إنها دالة أسية، لذا لرسمها يجب إنشاء جدول قيم يقيم الدالة في عدة نقاط:

$x= 0 \ \longrightarrow \ f(0)= \left(\cfrac{1}{2}\right)^0+3 = 4$

$x= 1 \ \longrightarrow \ f(1)= \left(\cfrac{1}{2}\right)^1+3 = 3,5$

$x= 2 \ \longrightarrow \ f(2)= \left(\cfrac{1}{2}\right)^2+3 = 3,25$

$x= -1 \ \longrightarrow \ f(-1)= \left(\cfrac{1}{2}\right)^{-1}+3 = 5$

$x= -2 \ \longrightarrow \ f(-2)= \left(\cfrac{1}{2}\right)^{-2}+3 = 7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 4 \\ 1 & 3,5 \\ 2 & 3,25 \\ -1 & 5 \\ -2 & 7 \end{array}$

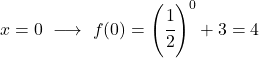
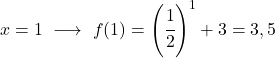
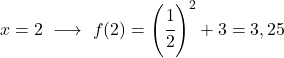
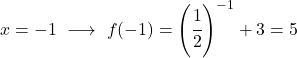
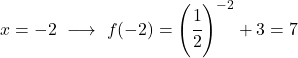
أخيرًا، نمثل النقاط التي تم الحصول عليها على الرسم البياني ونرسم الدالة:

لاحظ أن الدالة الموجودة على اليسار تنمو بشكل غير محدود إلى ما لا نهاية. من ناحية أخرى، على اليمين، تقل الدالة ولكنها لا تتجاوز 3 أبدًا. في الواقع، الدالة لها خط تقارب أفقي عند y=3.

في هذه الحالة، يكون الخط المقارب الأفقي عند y=3 بدلاً من المحور X لأنه تم نقل الدالة رأسيًا ثلاث وحدات لأعلى.

التمرين 4

حل المشكلة التالية فيما يتعلق بالوظائف الأسية.

تحديد قيمة
$k$

بحيث تمر الدالة الأسية التالية بالنقطة (2.8).

$f(x)=k\cdot 2^x$

انظر الحل

يجب أن تمر الدالة بالنقطة (2,8)، حتى نتمكن من استبدال قيم x و f(x) للنقطة في الدالة لإيجاد قيمة الثابت k:

$f(x)=k\cdot 2^x \ \xrightarrow{x \ = \ 2 \ ; \ f(x) \ = \ 8} \ 8 = k \cdot 2^2$

والآن نحل المعادلة الناتجة:

$8 = k \cdot 2^2$

$8 = k \cdot 4$

$\cfrac{8}{4} = k$

$\bm{ 2 = k}$

التمرين 5

حل المشكلة التالية فيما يتعلق بالوظائف الأسية.

تتكاثر جماعة النمل الأبيض وفقاً للوظيفة التالية:

$f(t)=3^{t+1}$

ذهب

$f(t)$

هو عدد النمل الأبيض و

$t$

لقد مر الوقت منذ أشهر.

كم عدد النمل الأبيض سيكون هناك بعد سنة واحدة؟

انظر الحل

لحساب عدد النمل الأبيض الذي سيكون موجودًا خلال عام، ما عليك سوى استبدال الوقت المنقضي (سنة واحدة) في الدالة. ولكن بما أن الدالة t هي الأشهر المنقضية وليس السنوات، فيجب أن نضع t = 12 حيث يوجد في السنة 12 شهرًا:

$f(t)=3^{t+1}$

$f(12)=3^{12+1}$

$f(12)=3^{13}$

نحل بالآلة الحاسبة:

$f(12)= 1594323$

إذن بعد عام واحد سيكون هناك 1,594,323 نملًا أبيضًا.

ما هي الدالة الأسية؟

أمثلة على الوظائف الأسية

خصائص الدوال الأسية

كيفية رسم دالة أسية

تمارين محلولة على الدوال الأسية

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

اترك تعليقاً إلغاء الرد