وظيفة غير عقلانية أو وظيفة جذرية -

تشرح هذه الصفحة ماهية الدالة غير المنطقية، والتي تسمى أيضًا الدالة الجذرية، بالإضافة إلى جميع خصائص هذا النوع من الوظائف. سوف تكتشف أيضًا كيفية حساب مجال الدوال الجذرية أو غير المنطقية، بالإضافة إلى ذلك، ستتمكن من رؤية كيفية تمثيلها على الرسم البياني مع الأمثلة والتدرب على التمارين والمسائل التي تم حلها خطوة بخطوة.

ما هي الوظيفة غير العقلانية (أو الجذرية)؟

دالة غير عقلانية تعني نفس دالة جذرية، وبالتالي فإنها تشترك في التعريف:

الدالة غير المنطقية ، وتسمى أيضًا دالة جذرية ، هي دالة تحتوي على المتغير المستقل x تحت رمز الجذر.

وكما نعلم بالفعل، فإن نتيجة الجذر يمكن أن تكون إيجابية أو سلبية. وبالتالي فإن تمثيل دالة غير عقلانية (أو جذرية) له منحنيان محتملان:

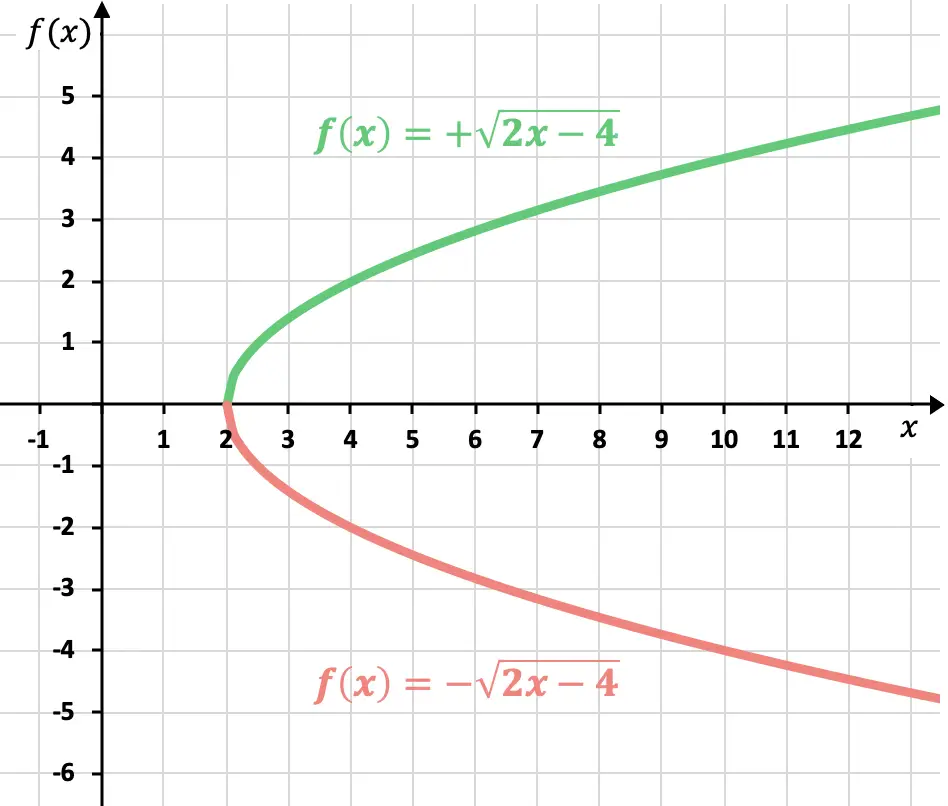
أمثلة على الوظائف غير العقلانية أو الجذرية

لكن إذا لم يتم تحديد الإشارة، فمن المفترض أن يتم تمثيل الدالة الإيجابية.

ومن ناحية أخرى، لا ينبغي الخلط بين الوظيفة غير العقلانية والوظيفة العقلانية. على الرغم من أن لديهم أسماء متشابهة جدًا، إلا أنهما نوعان مختلفان تمامًا من الوظائف.

مجال وظيفة غير عقلانية أو جذرية

يعتمد مجال الدالة ذات الجذور على تكافؤ مؤشر الجذر، أي أنه يعتمد على ما إذا كان مؤشر الجذر زوجيًا أم فرديًا.

مجال الدالة ذات جذر الفهرس الزوجي

كما تعلم جيدًا، لا يوجد جذر (زوجي) للرقم السالب. لذلك، ستظل الدالة الجذرية ذات الفهرس الزوجي موجودة طالما أن محتواها يساوي أو أكبر من 0.

على سبيل المثال، دعونا نرى كيف يتم حساب مجال الدالة الجذرية أو غير النسبية التالية:

$f(x)=\sqrt{x-4}$

هذه دالة جذرية ذات فهرس زوجي، لذا يجب أن ننظر إلى متى يكون محتواها موجبًا أو صفرًا :

$x-4\ge 0$

نحن نحل عدم المساواة:

$x\ge 4$

إذن ستكون الدالة موجودة عندما تكون x أكبر من أو تساوي 4، ويشار إليها بالفاصل الزمني التالي:

$\text{Dom } f= [4,+\infty)$

مجال الدالة ذات جذر الفهرس الفردي

لا تواجه الدوال غير المنطقية ذات الفهرس الفردي هذه المشكلة، نظرًا لوجود جذر الفهرس الفردي لعدد سالب:

$\sqrt[3]{-8}=-2$

ولذلك، توجد وظائف جذرية للمؤشر الفردي لأي قيمة لـ x . أو بمعنى آخر، يتكون المجال من أرقام حقيقية فقط .

على سبيل المثال، سوف نحسب مجال تعريف الدالة الجذرية التالية التي يكون فهرسها فرديًا:

$f(x)=\sqrt[3]{3x-4}$

نظرًا لأنها دالة غير منطقية ذات فهرس فردي، فإن مجالها يتكون من أرقام حقيقية:

$\text{Dom } f= \mathbb{R}$

كيفية تمثيل وظيفة غير عقلانية أو جذرية

دعونا نرى كيفية تمثيل دالة ذات جذور على الرسم البياني باستخدام مثال.

ارسم الدالة الجذرية أو غير المنطقية التالية على الرسم البياني:

$f(x)=\sqrt{x+2}$

أول شيء يجب فعله هو إيجاد مجال الدالة. وبما أنه جذر تربيعي، فإن كل ما يحتوي عليه يجب أن يكون موجبًا، لأنه لا يوجد جذر تربيعي لعدد سالب. ولذلك فإن الدالة الجذرية ستكون موجودة طالما أن محتواها يساوي أو أكبر من 0:

$x+2\ge 0$

$x\ge -2$

وبالتالي، فإن مجال الدالة يتكون من جميع الأرقام الأكبر من أو تساوي -2. هذا لأقول:

$\text{Dom } f = [-2,+\infty)$

بمجرد أن نعرف مجال الدالة، نقوم بإنشاء جدول القيم. من الواضح أنه كلما زاد عدد النقاط التي نحسبها، أصبح تمثيل الدالة أكثر دقة. لكن حساب 3 أو 4 نقاط في الفاصل الزمني للمجال يكفي:

$x= -2 \ \longrightarrow \ f(-2)=\sqrt{-2+2}= 0$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{-1+2}= 1$

$x= 2 \ \longrightarrow \ f(2)=\sqrt{2+2}= 2$

$x= 7 \ \longrightarrow \ f(7)=\sqrt{7+2}= 3$

$\begin{array}{c|c} x & f(x) \\ \hline -2 & 0 \\ -1 & 1 \\ 2 & 2 \\ 7 & 3 \end{array}$

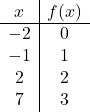
نحن الآن نمثل النقاط التي تم الحصول عليها على الرسم البياني :

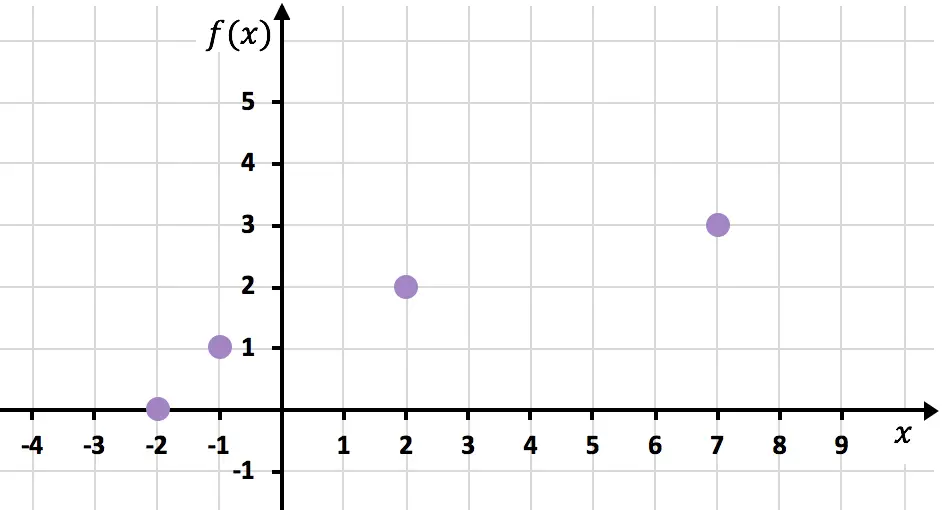
وأخيرًا، نربط النقاط ونمد المنحنى للإشارة إلى استمرار نمو الدالة:

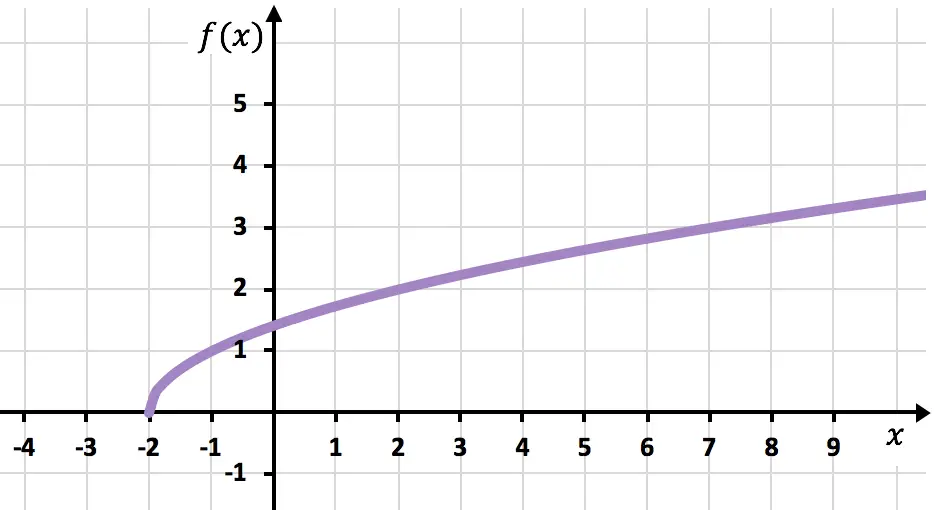
مثال على التمثيل الرسومي لوظيفة جذرية أو غير عقلانية

تمارين محلولة على الدوال غير العقلانية أو الجذرية

التمرين 1

أوجد مجال الدالة الجذرية التالية:

$\sqrt{3x+6}$

انظر الحل

الجذر التربيعي لعدد سالب غير موجود. لذلك، ستكون الدالة موجودة عندما يكون الوسيط الجذر موجبًا أو صفرًا:

$3x+6 \ge 0$

$3x \ge -6$

$x \ge \cfrac{-6}{3}$

$x \ge -2$

$\mathbf{Dom } \ \bm{f = [-2,+\infty)}$

تمرين 2

أوجد مجال الدالة غير المنطقية التالية:

$\sqrt{-x+2}$

انظر الحل

الجذر التربيعي لعدد سالب ليس له حل حقيقي. لذلك، ستكون الدالة موجودة طالما أن محتوى الجذر موجب أو صفر:

$-x+2\ge 0$

$-x\ge -2$

$x\le\cfrac{-2}{-1}=2$

تذكر أنه إذا قمنا بتغيير أضلاع عدد سالب يضرب أو يقسم في متباينة، فيجب علينا أيضًا تدوير إشارة المتباينة.

$x\le2$

$\mathbf{Dom } \ \bm{f = (-\infty,2]}$

التمرين 3

ارسم الدالة غير المنطقية التالية على الرسم البياني:

$f(x)= \sqrt{x-1}$

انظر الحل

أولًا يجب علينا حساب مجال الدالة:

$x-1\ge 0$

$x\ge 1$

$\text{Dom } f = [1,+\infty)$

نقوم الآن بإنشاء مصفوفة من القيم بإعطاء قيم الدالة في نطاق المجال:

$x= 1 \ \longrightarrow \ f(1)= \sqrt{1-1}=0$

$x= 2 \ \longrightarrow \ f(2)= \sqrt{2-1}=1$

$x= 5 \ \longrightarrow \ f(5)= \sqrt{5-1}=2$

$x= 10 \ \longrightarrow \ f(10)= \sqrt{10-1}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 2 & 1 \\ 5 & 2 \\ 10 & 3 \end{array}$

أخيرًا، نرسم النقاط ونرسم الدالة على الرسم البياني:

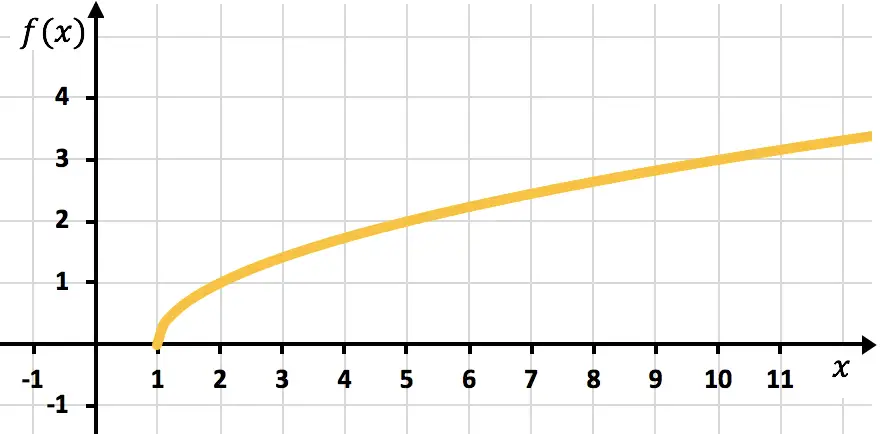
تمرين حل خطوة بخطوة لدالة غير عقلانية أو جذرية

التمرين 4

ارسم بيانيًا الدالة غير المنطقية أو الجذرية التالية:

$f(x)= -2\sqrt{x}+3$

انظر الحل

أولًا يجب علينا حساب مجال الدالة:

$x\ge 0$

$\text{Dom } f = [0,+\infty)$

نقوم الآن بإنشاء مصفوفة من القيم بإعطاء قيم الدالة في نطاق المجال:

$x= 0 \ \longrightarrow \ f(0)= -2\sqrt{0}+3=3$

$x= 1 \ \longrightarrow \ f(1)= -2\sqrt{1}+3=1$

$x= 4 \ \longrightarrow \ f(4)= -2\sqrt{4}+3=-1$

$x= 9 \ \longrightarrow \ f(9)= -2\sqrt{9}+3=-3$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 3 \\ 1 & 1 \\ 4 & -1 \\ 9 & -3 \end{array}$

أخيرًا، نرسم النقاط ونرسم الدالة على الرسم البياني:

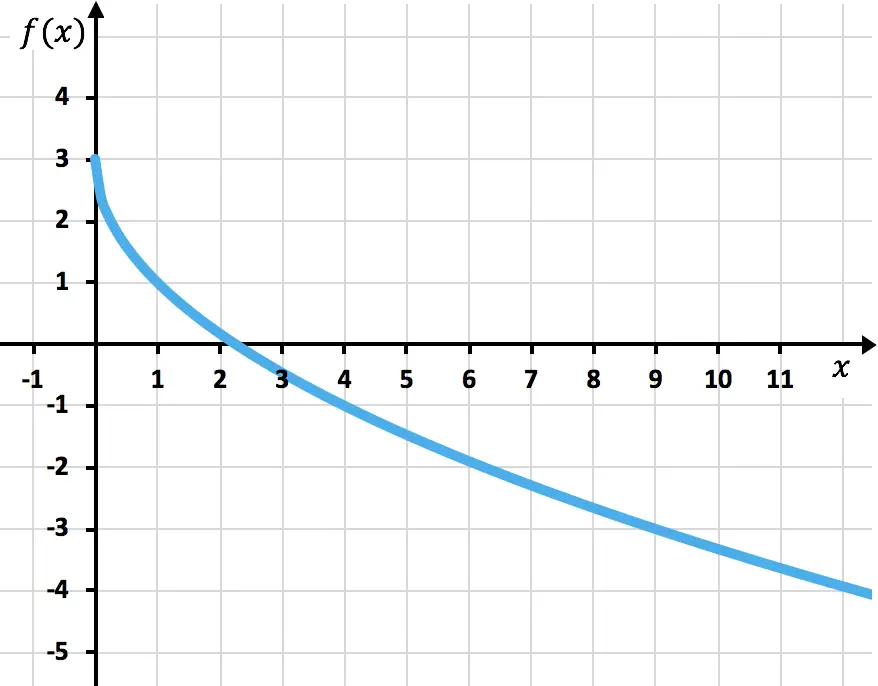
التمرين 5

ارسم بيانيًا الدالة غير المنطقية أو الجذرية التالية:

$f(x)= \sqrt{-x+5}$

انظر الحل

قبل رسم الدالة، نحتاج إلى حساب مجال الدالة:

$-x+5\ge 0$

$-x\ge -5$

$x\le\cfrac{-5}{-1}=5$

تذكر أنه إذا قمنا بتغيير أضلاع عدد سالب يضرب أو يقسم في متباينة، فيجب علينا أيضًا تغيير إشارة المتباينة.

$x\le5$

$\text{Dom } f = (-\infty,5]$

الآن نقوم ببناء جدول القيم من خلال تقييم الدالة عند النقاط التي تنتمي إلى مجال الدالة:

$x= 5 \ \longrightarrow \ f(5)=\sqrt{-5+5}=0$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{-4+5}=1$

$x= 1 \ \longrightarrow \ f(1)=\sqrt{-1+5}=2$

$x= -4 \ \longrightarrow \ f(-4)=\sqrt{-(-4)+5}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 5 & 0 \\ 4 & 1 \\ 1 & 2 \\ -4 & 3 \end{array}$

وأخيرًا، ما عليك سوى تمثيل النقاط ورسم الدالة على الرسم البياني:

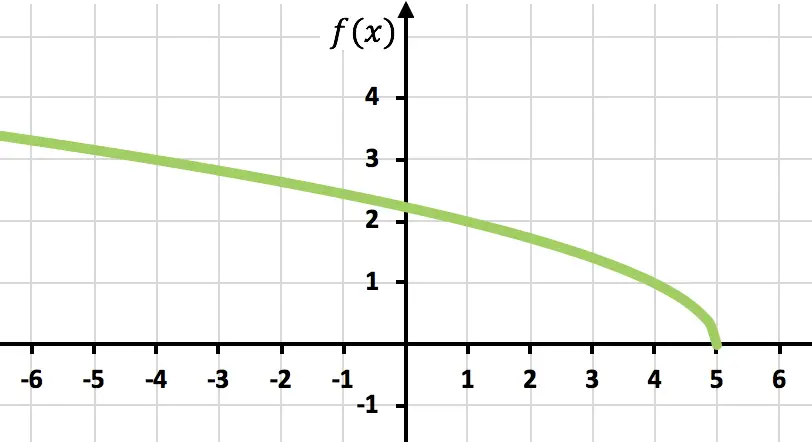
تمارين محددة للوظائف الجذرية أو غير العقلانية

التمرين 6

ارسم الدالة غير المنطقية أو الجذرية التالية على الرسم البياني:

$f(x)= \sqrt{x^2-5x+4}$

انظر الحل

يجب علينا أولاً حساب مجال الوظيفة:

$x^2-5x+4\ge 0$

في هذه الحالة حصلنا على متباينة من الدرجة الثانية، لذا نحتاج إلى تطبيق صيغة المعادلات التربيعية لحلها:

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle x=\cfrac{-(-5)\pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1} = \cfrac{5\pm 3}{2} =\begin{cases} 4 \\[2ex] 1 \end{cases}$

نقسم الخط إلى ثلاث قطع مع الحصول على الجذور:

ونعوض برقم لكل قسم من المتراجحة لمعرفة الأقسام التي تحقق المتراجحة وبالتالي تنتمي إلى المجال:

$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 0} <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-7c214e08b91825263231bc6eddbbdee1_l3.png" height="54" width="404" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[0^2-5\cdot 0+4\ge 0 \ \longrightarrow \ 4\ge 0 $ ✅$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 2}\]" title="Rendered by QuickLaTeX.com"/> 2^2-5\cdot 2+4\ge 0 \ \longrightarrow \ -10\ \cancel{\ge } \ 0″ title=”Rendered by QuickLaTeX.com”> <p style=$ ❌

$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 5}$

$5^2-5\cdot 5+4\ge 0 \ \longrightarrow \ 4\ge 0$

✅

وبالتالي فإن الأقسام التي تحترم عدم المساواة هي تلك الخاصة بالجانبين:

وبالتالي فإن مجال الدالة هو:

$\text{Dom } f = (-\infty,1]\cup [4,+\infty)$

بمجرد أن نحسب مجال الدالة، نقوم ببناء جدول قيم يعطي قيم الدالة في فترة المجال:

$x= 1 \ \longrightarrow \ f(1)=\sqrt{1^2-5\cdot 1+4} =0$

$x= 0 \ \longrightarrow \ f(0)=\sqrt{0^2-5\cdot 0+4} =2$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{(-1)^2-5\cdot (-1)+4} =3,16$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{4^2-5\cdot 4+4} =0$

$x= 5 \ \longrightarrow \ f(5)=\sqrt{5^2-5\cdot 5+4} =2$

$x= 6 \ \longrightarrow \ f(6)=\sqrt{6^2-5\cdot 6+4} =3,16$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 0 & 2 \\ -1 & 3,16 \\ 4 & 0 \\ 5 & 2 \\ 6 & 3,16 \\ \end{array}$

أخيرًا، نمثل النقاط التي تم الحصول عليها على الرسم البياني ونرسم الدالة:

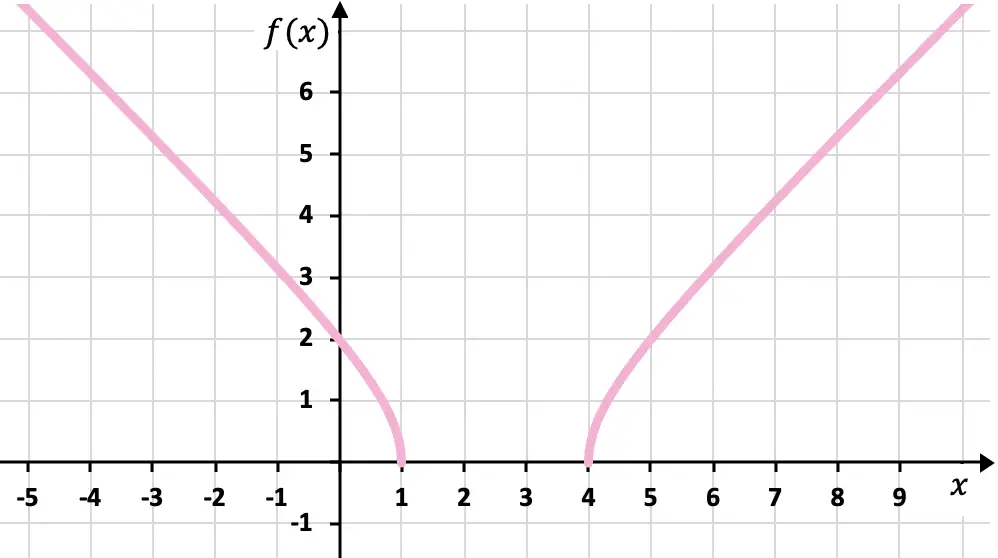
رسم بياني لوظيفة غير عقلانية أو جذرية مع مؤشر زوجي

التمرين 7

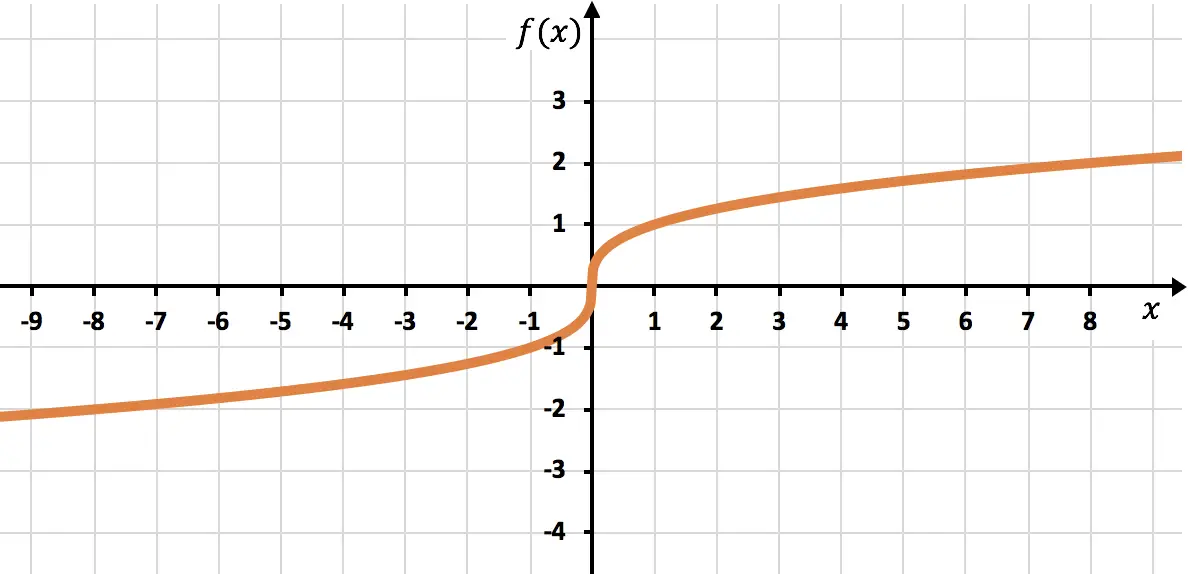
مثّل على الرسم البياني الدالة التالية المكونة من جذر:

$f(x)= \sqrt[3]{x}$

انظر الحل

وهي دالة غير نسبية جذرها ذو فهرس فردي، وبالتالي فإن مجال الدالة يتكون من أعداد حقيقية:

$\text{Dom } f = \mathbb{R}$

ومن ثم يمكننا أن نأخذ أي نقطة لإنشاء جدول القيم. وفي هذه الحالة سنبحث عن نقاط عديدة لأنه جذر تكعيبي:

$x= 0 \ \longrightarrow \ f(0)= \sqrt[3]{0} = 0$

$x= 0,5 \ \longrightarrow \ f(0,5)= \sqrt[3]{0,5} = 0,79$

$x= -0,5 \ \longrightarrow \ f(-0,5)= \sqrt[3]{-0,5} = -0,79$

$x= 1 \ \longrightarrow \ f(1)= \sqrt[3]{1} = 1$

$x= -1 \ \longrightarrow \ f(-1)= \sqrt[3]{-1} = -1$

$x= 8 \ \longrightarrow \ f(8)= \sqrt[3]{8} = 2$

$x= -8 \ \longrightarrow \ f(-8)= \sqrt[3]{-8} = -2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 0 \\ 0,5 & 0,79 \\ -0,5 & -0,79 \\ 1 & 1 \\ -1 & -1 \\ 8 & 2 \\ -8 & -2 \end{array}$

أخيرًا، نرسم النقاط التي تم العثور عليها ونرسم الدالة على الرسم البياني:

رسم بياني لدالة غير عقلانية أو جذرية بمؤشر فردي

التمرين 8

حل المشكلة التالية المتعلقة بالدوال غير العقلانية (أو الجذرية):

يتم تحديد استهلاك بطارية الهاتف الخليوي من خلال الوظيفة التالية:

$f(t)=\sqrt{x-K \vphantom{(-K)}}$

حيث يتم التعبير عن الاستهلاك بالمللي أمبير (mA) و

$t$

هو الوقت المنقضي بالدقائق.

تحديد قيمة الثابت

$K$

بحيث يكون الاستهلاك بعد 4 دقائق 35 مللي أمبير.

انظر الحل

أنه بعد 4 دقائق يكون الاستهلاك 35 مللي أمبير يعني أنه عندما يكون t 4، يكون f(t) 35. إذن f(4)=35.

$f(4)=\sqrt{4-K} = 35$

$\sqrt{4-K} = 35$

الآن علينا حل المعادلة التي حصلنا عليها. إذا نظرت عن كثب، فهي معادلة غير منطقية لأنها تحتوي على جذر. في هذا النوع من المعادلات، أول ما يجب فعله هو عزل جذر أحد الطرفين، وهو في هذه الحالة معزول بالفعل. بعد العزلة، يجب علينا تربيع طرفي المعادلة:

$\left( \sqrt{4-K} \right)^2= 35^2$