المضاعف المشترك الأصغر (LCM) لعددين أو أكثر هو المضاعف الأصغر (غير الصفر) المشترك بين هذه الأرقام. إنها العملية العكسية للقاسم المشترك الأكبر ، على الرغم من أنها تحسب باستخدام طرق مماثلة. إذا كنت تريد معرفة كيفية حساب المضاعف المشترك الأصغر، فنوصيك بمواصلة القراءة، لأننا سنشرح في هذه المقالة جميع الإجراءات (من الأبسط إلى الأكثر تعقيدًا) للعثور على أصغر مضاعف مشترك لمجموعة من الأرقام.
حاسبة lcm
قبل أن نبدأ الحديث عن كيفية الحصول على lcm، نريد منك أن تعلم أنه في هذه الصفحة لدينا آلة حاسبة متعددة مشتركة على الأقل . باستخدامه، ستتمكن من حساب lcm لجميع الأرقام التي تريدها، وبهذه الطريقة يمكنك مقارنة نتائج تمارينك لمعرفة ما إذا كنت قد قمت بحلها بشكل صحيح.
كيفية حساب المضاعف المشترك الأصغر؟
للعثور على المضاعف المشترك الأصغر لعددين أو أكثر، عليك اتباع إحدى الطرق الثلاث التي سنشرحها أدناه. بعد ذلك، عندما نقوم بتفصيل كل إجراء من الإجراءات التي يمكنك اختيارها، سنخبرك أيضًا بمزاياها وعيوبها. بهذه الطريقة ستعرف أي واحد تختاره في كل موقف لحل LCM المعني بسهولة وسرعة.
الطريقة الأولى: قائمة متعددة
الطريقة الأولى هي إنشاء قائمة بمضاعفات الأرقام التي تريد حسابها في المضاعف المشترك الأصغر. ثم عليك أن تجد أصغر قيمة تتكرر في جميع القوائم ، وبهذه الطريقة سيكون لديك أصغر مضاعف مشترك. ثم سنراها بمثال: لسم (5، 6).
مضاعفات العدد 5: 5، 10، 15، 20، 25، 30 ، 35، 40...
مضاعفات العدد 6: 6، 12، 18، 24، 30 ، 36، 42، 48...
نحن نبحث عن أصغر مشترك ولدينا بالفعل lcm.
سم (5، 6) = 30
الطريقة الثانية: التحلل العاملي
ثانيًا، يمكننا اختيار تحليل الأعداد إلى عوامل. وبشكل أكثر تحديدًا، ستسهل هذه الطريقة حساب PCM للأعداد الكبيرة . نظرًا لأن اتباع الطريقة الأولى عند تنفيذ lcm لأعداد كبيرة يمكن أن يكون بطيئًا ومملًا، وذلك ببساطة لأنه سيتعين علينا كتابة قوائم طويلة جدًا من المضاعفات. يمكن أن يكون فهم هذا الإجراء الثاني أكثر تعقيدًا في البداية، ولكن عندما تفهم الآليات، سيكون له العديد من المزايا مقارنة بالإجراء السابق. ومع ذلك، دعونا نرى الإجراء الذي يجب اتباعه:
- التحليل العاملي: ستكون الخطوة الأولى هي تحليل جميع الأرقام التي سندرجها في المضاعف المشترك الأصغر إلى عوامل أولية. في حال كنت لا تعرف كيفية تحليل عدد مضروبا ، ننصحك بالدخول إلى هذا الرابط الأخير، حيث ستجد شرحا من الطراز الأول لكيفية تبسيط الأرقام بسرعة وكفاءة.
- إنشاء تعبير رياضي واحد: عندما يتم التعبير عن جميع الأرقام كعوامل أولية، سنختار الأرقام المشتركة وغير المشتركة مرفوعة إلى أكبر أس. ثم تكتبها كتعبير رياضي واحد، وفي النهاية تقوم بحل الضرب و/أو القوى الضرورية. وسيكون لديك بالفعل القيمة العددية لـ lcm.
الطريقة الثالثة: الصيغة الرياضية
هناك طريقة أخيرة للحصول على المضاعف المشترك الأصغر، وهي استخدام GCD والمعادلة الرياضية التالية:
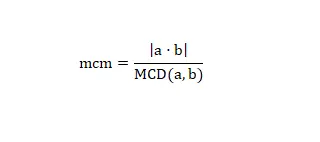
باستخدام هذه الصيغة يمكننا حساب lcm لأي رقم. دعونا نرى مثالًا حقيقيًا، إذا أردنا حساب lcm (2.6)، فنحن ببساطة بحاجة إلى حل العملية (2 × 6) / 2 = 6. وسنكون قد حللنا العملية الحسابية بالفعل، كما ترون، فهي طريقة بسيطة وبسرعة إذا كان لديك GCD أو يمكنك حسابه بسهولة.
نصائح لحساب lcm بسرعة
عندما تتقن الطرق الثلاث التي شرحناها للتو، ننصحك بقراءة خصائص المضاعف المشترك الأصغر الذي سنتحدث عنه الآن. نظرًا لأنه بفضلهم ستتمكن من تحديد بعض المواقف المحددة التي يمكن فيها حساب LCM بسرعة كبيرة، دون الحاجة إلى استخدام الاستراتيجيات الموضحة بالفعل.
- الرقم الأول القابل للقسمة على الثاني: إذا أردنا حساب أصغر مضاعف مشترك لـ a وb عندما يقسم a b، فإن ppcm لهذين الرقمين سيكون الأكبر (في هذه الحالة b). على سبيل المثال، إذا كنت تريد حساب lcm للعددين 2 و8، فستكون النتيجة هي الأكبر، وبالتالي 8.
- رقمان أوليان: في حالة العثور على رقمين أوليين ، فإن أسرع طريقة هي ضربهما معًا وستكون النتيجة ppcm. وهذا أمر منطقي، لأن القاسم المشترك الأكبر له هو 1، مما يعني أننا لن نكون قادرين على تحليل الرقم إلى عوامل أبسط من الرقم نفسه، وبالتالي، لن نكون قادرين إلا على ضربهم معًا. على سبيل المثال، المضاعف المشترك الأصغر للرقمين 3 و5 سيكون نتيجة حاصل ضربهما: 3 × 5 = 15.
كيفية الحصول على المضاعف المشترك الأصغر في الكسور؟
عندما نريد حل عملية جمع أو طرح الكسور، نحتاج إلى حساب المقام المشترك الأصغر، وهو نفس lcm، لكنه يطبق على الكسور. في الأساس، نحن نبحث عن lcm للمقامين حتى نتمكن بعد ذلك من التعبير عن المجموع في صورة كسر واحد. إذا كنت تريد أن ترى كيف يتم تطبيق القاسم المشترك الأدنى على حساب الكسر الحقيقي، يمكنك الدخول إلى هذا الرابط .
Lcm على الآلة الحاسبة العلمية
يتيح لك مفتاح LCM، الموجود في أي آلة حاسبة علمية، حساب أصغر مضاعف مشترك لعددين صحيحين. في حالة الآلات الحاسبة من Casio، يكون بناء الجملة أو الإجراء الذي يتعين عليك اتباعه كما يلي. أولاً، اضغط على APHA + MCM (سيكون هذا المفتاح الأخير باللون البني). بمجرد الانتهاء من ذلك، يمكنك إدخال كلا الرقمين، ولكن تذكر أنه يجب عليك الفصل بينهما بفاصلة ( SHIFT + , ). وأخيرا، سوف تحصل على أصغر مضاعف مشترك من خلال النقر على زر يساوي.
تمارين LCM تم حلها خطوة بخطوة
بعد ذلك، سنعرض لك ثلاثة أمثلة على المضاعف المشترك الأصغر الذي تم حله خطوة بخطوة . بهذه الطريقة يمكنك محاولة حل هذه المشكلات وممارسة القليل مما شرحناه في هذه المقالة. من المهم أن تحاول حل التمارين إذا كنت تريد استيعاب المفاهيم، لأنه من الضروري تطبيق النظرية على الواقع. ومع ذلك، نسمح لك بالتدرب على التمارين:
احسب lcm للعددين 4 و6
مضاعفات 4: 4، 8، 12 ، 16، 20، 24 ، 28، 32، 36 ...
مضاعفات 6: 6، 12 ، 18، 24 ، 30، 36 ، 42، 48...
سوف نحل هذا التمرين باستخدام الطريقة الأولى (قائمة المضاعفات). للبدء، نحتاج إلى تحديد ما هو مشترك بين القائمتين وسنختار القائمة الأصغر. إذن المضاعف المشترك الأصغر للعددين 4 و 6 هو 12 .
احسب lcm للعددين 6 و9
مضاعفات 6: 6، 12، 18 ، 24، 30، 36 ، 42، 48...
مضاعفات العدد 9: 9، 18 ، 27، 36 ، 45، 54، 63، 72...
سوف نقوم بحل هذا التمرين الثاني بنفس طريقة التمرين السابق. للبدء، نحتاج إلى تحديد القائمة الأكثر شيوعًا من القائمتين وسنختار القائمة الصغيرة. إذن المضاعف المشترك الأصغر للعددين 6 و 9 هو 18 .
احسب lcm 30 و 40
التحليل الأولي للعدد 30: 2 × 3 × 5
التحليل الأولي لـ 40: 2³ × 5
سوف نحل هذا التمرين الأخير باستخدام طريقة التحلل العاملي. لذلك، يجب علينا أولًا التعبير عن العددين بالعوامل الأولية وسنختار المشترك وغير المشترك مرفوعًا للأس الأكبر. إذن lcm لـ 30 و40 هو 2³ × 3 × 5 = 120.