▷ ما هي وكيفية تمثيل دالة تربيعية (أو قطع مكافئ)

تشرح هذه الصفحة ماهية الدالة التربيعية بالإضافة إلى جميع خصائصها: الانحناء، الرأس، نقاط التقاطع مع المحاور، إلخ. سوف تتعلم أيضًا كيفية تمثيل دالة تربيعية على الرسم البياني. وأخيرًا، يمكنك التدرب باستخدام الأمثلة والتمارين خطوة بخطوة والمسائل المتعلقة بالدوال التربيعية.

ما هي الدالة التربيعية؟

تعريف الدالة التربيعية هو كما يلي:

في الرياضيات، الدالة التربيعية (أو المكافئة) هي دالة متعددة الحدود من الدرجة الثانية، أي دالة يكون الحد الأعلى فيها من الدرجة الثانية. ولذلك، فإن صيغة الدالة التربيعية هي:

$f(x)=ax^2+bx+c$

ذهب:

$ax^2$

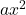
هو الحد التربيعي.
$bx$

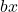
هو المصطلح الخطي.
$c$

هو المصطلح المستقل.

يتكون مجال الدالة التربيعية دائمًا من أعداد حقيقية.

$\text{Dom } f=\mathbff{R}$

تقعر وتحدب الدالة التربيعية

يعد تحليل انحناء الدالة التربيعية أو القطع المكافئ أمرًا بسيطًا للغاية، لأنه يعتمد فقط على المعامل التربيعي.

إذا كان المعامل
$a$

موجبة، والدالة التربيعية محدبة (في الشكل

$\bm{\cup}$

). وبالتالي فإن القمة هي الحد الأدنى.
إذا كان المعامل
$a$

سالبة، والدالة التربيعية مقعرة (على شكل

$\bm{\cap}$

). وبالتالي فإن الذروة هي الحد الأقصى.

ملاحظة: المجتمع الرياضي لا يزال غير موافق تمامًا، ولذلك يقول بعض الأساتذة عكس ذلك: فهم يسمون الدالة المقعرة التي لها شكل

$\bm{\cup}$

، والدالة المحدبة التي لها شكل

$\bm{\cap}$

. وفي كل الأحوال، المهم هو الشكل الذي له الوظيفة، مهما كان الاسم.

قمة الدالة التربيعية

لتمثيل دالة تربيعية، من الضروري معرفة إحداثيات رأس القطع المكافئ.

للعثور على رأس دالة تربيعية، نحتاج إلى حساب الإحداثي X للنقطة باستخدام الصيغة التالية:

$\displaystyle x=\frac{-b}{2a}$

ومن ثم يمكننا إيجاد إحداثيات الرأس الأخرى عن طريق حساب صورة الدالة عند تلك النقطة:

$\displaystyle f\left(\frac{-b}{2a}\right)$

وبالتالي فإن إحداثيات رأس الدالة التربيعية (أو القطع المكافئ) هي:

$\displaystyle \left(\frac{-b}{2a} \ , \ f\left(\frac{-b}{2a}\right)\right)$

نقاط القطع مع محاور الدالة التربيعية

يتقاطع القطع المكافئ دائمًا مع المحور ص (المحور ص)، ويحدث هذا عندما

$x=0.$

لذلك، لحساب نقطة القطع لدالة تربيعية مع المحور Y، يجب حلها

$f(0).$

على سبيل المثال، نقطة التقاطع مع محور OY للدالة التربيعية التالية هي:

$f(x)=x^2-2x+1$

$f(0)=0^2-2\cdot 0+1 = 1$

$\bm{(0,1)}$

من ناحية أخرى، فإن نقطة القطع للدالة التربيعية مع المحور السيني (المحور السيني) تحدث عندما

$f(x)=0.$

إذن لحساب نقطة التقاطع مع المحور X عليك حل المعادلة

$f(x)=0.$

على سبيل المثال، فيما يلي حساب نقطة القطع مع محور OX لنفس الدالة التربيعية:

$f(x)=x^2-2x+1$

$0=x^2-2x+1$

نحل المعادلة التربيعية بالصيغة العامة:

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$x=\cfrac{-(-2)\pm \sqrt{(-2)^2-4\cdot 1\cdot1}}{2\cdot 1} =\cfrac{2\pm 0}{2} = 1$

وبالتالي فإن نقطة تقاطع الدالة التربيعية مع المحور X هي:

$\bm{(1,0)}$

في هذه الحالة، حصلنا على حل واحد فقط للمعادلة التربيعية، لكن كان من الممكن أن نحصل على حلين. في هذه الحالة، هذا يعني أن الدالة التربيعية تتقاطع مع المحور X عند نقطتين مختلفتين.

مثال لتمثيل دالة تربيعية أو مكافئة

دعونا نرى كيفية تمثيل دالة تربيعية على الرسم البياني باستخدام مثال.

رسم بياني للوظيفة التالية:

$f(x)=x^2-4x+5$

أول شيء يجب فعله هو حساب رأس القطع المكافئ. للقيام بذلك، نستخدم الصيغة التي رأيناها أعلاه:

$x = \cfrac{-b}{2a} = \cfrac{-(-4)}{2\cdot 1}= \cfrac{4}{2}= 2$

بمجرد أن نعرف أين سيكون الرأس، نحتاج إلى إنشاء جدول القيم: نحسب قيمة الدالة عند الرأس والنقاط المحيطة به:

$f(x)=x^2-4x+5$

$x= 2 \ \longrightarrow \ f(2) = 2^2-4\cdot2+5=1$

$x= 1 \ \longrightarrow \ f(1)=1^2-4\cdot1+5=2$

$x= 3 \ \longrightarrow \ f(3) = 3^2-4\cdot3+5=2$

$x= 0 \ \longrightarrow \ f(0) = 0^2-4\cdot0+5=5$

$x= 4 \ \longrightarrow \ f(4) = 4^2-4\cdot4+5=5$

$\begin{array}{c|c} x & f(x) \\ \hline 2 & 1 \\ 1 & 2 \\ 3 & 2 \\ 0 & 5 \\ 4 & 5 \end{array}$

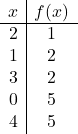
يمكنك أيضًا حساب نقاط القطع للدالة التربيعية باستخدام المحاور الديكارتية لرسم القطع المكافئ بشكل أفضل، لكن هذا ليس ضروريًا تمامًا.

نحن الآن نمثل النقاط التي تم الحصول عليها على الرسم البياني :

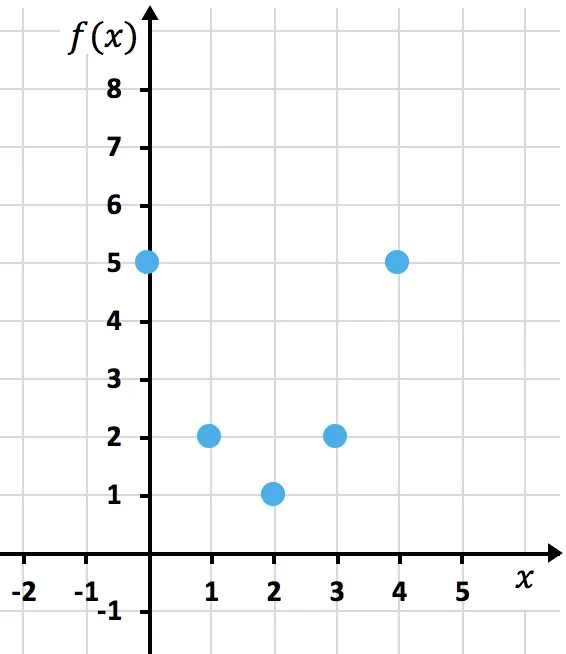
مثال على كيفية تمثيل دالة تربيعية أو مكافئة

وأخيرًا، نربط النقاط التي تشكل القطع المكافئ. ثم نطيل فروع القطع المكافئ للدلالة على استمراره للأعلى:

تمارين محلولة على الدوال التربيعية

التمرين 1

أوجد رأس الدالة التربيعية التالية:

$f(x)=2x^2+8x+4$

انظر الحل

نحسب أولاً إحداثي X للرأس باستخدام الصيغة:

$x = \cfrac{-b}{2a} = \cfrac{-8}{2\cdot 2} = \cfrac{-8}{4} = -2$

والآن نحسب الإحداثيات الأخرى من خلال تقييم الدالة عند النقطة:

$\begin{aligned} f(-2) & =2(-2)^2+8(-2)+4 \\[1.7ex] & = 2 \cdot 4 - 16 +4 \\[1.7ex] & = 8-16+4 \\[1.7ex] & = -4 \end{aligned}$

وبالتالي فإن قمة الدالة التربيعية هي:

$\bm{(-2,-4)}$

تمرين 2

أوجد نقاط القطع للدالة التالية مع المحاور:

$f(x)=x^2-4x+3$

انظر الحل

لحساب نقطة القطع مع المحور Y، نحتاج إلى الحساب

$f(0):$

$f(0)=0^2-4\cdot 0+3 = 3$

وبالتالي تمر الدالة عبر المحور Y عند النقطة:

$\bm{(0,3)}$

ولإيجاد نقاط القطع مع المحور X علينا حلها

$f(x)=0:$

$f(x)=x^2-4x+3$

$0=x^2-4x+3$

نحسب جذور المعادلة التربيعية بالصيغة:

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle x=\cfrac{-(-4)\pm \sqrt{(-4)^2-4\cdot 1\cdot 3}}{2\cdot 1} =\cfrac{4\pm 2}{2} = \begin{cases} 3 \\[2ex] 1 \end{cases}$

وبالتالي فإن الدالة تقطع المحور X عند نقطتين:

$\bm{(1,0) \qquad (3,0)}$

التمرين 3

ارسم بيانيًا الدالة التربيعية التالية:

$f(x)=-x^2+4x+1$

انظر الحل

هذه دالة تربيعية. وبالتالي، لتمثيله، يجب عليك أولاً حساب الإحداثيات الإحداثية لرأس القطع المكافئ بالصيغة:

$x = \cfrac{-b}{2a} = \cfrac{-4}{2\cdot (-1)} = \cfrac{-4}{-2} = 2$

الآن نقوم بإنشاء جدول القيم. للقيام بذلك، نحسب قيمة

$f(x)$

في الأعلى وحول الأعلى:

$x= 2 \ \longrightarrow \ f(2)=-2^2+4\cdot2+1 = 5$

$x= 1 \ \longrightarrow \ f(1)=-1^2+4\cdot1+1 = 4$

$x= 3 \ \longrightarrow \ f(3)=-3^2+4\cdot3+1 =4$

$x= 0 \ \longrightarrow \ f(0)=-0^2+4\cdot0+1 = 1$

$x= 4 \ \longrightarrow \ f(4)=-4^2+4\cdot4+1 = 1$

$\begin{array}{c|c} x & f(x) \\ \hline 2 & 5 \\ 1 & 4 \\ 3 & 4 \\ 0 & 1 \\ 4 & 1 \end{array}$

وأخيرًا، نرسم النقاط على الرسم البياني ونرسم القطع المكافئ:

التمرين 4

ارسم بيانيًا الدالة التربيعية التالية:

$f(x)=-2x^2-8x-1$

انظر الحل

هذه وظيفة من الدرجة الثانية. وبالتالي، لتمثيله، يجب عليك أولاً العثور على الإحداثيات الإحداثية لرأس القطع المكافئ بالصيغة:

$x = \cfrac{-b}{2a} = \cfrac{-(-8)}{2\cdot (-2)} = \cfrac{+8}{-4} = -2$

الآن نقوم ببناء جدول القيم. للقيام بذلك، نحسب قيمة

$f(x)$

في الأعلى وحول الأعلى:

$x= -2 \ \longrightarrow \ f(-2)=-2(-2)^2-8\cdot(-2)-1 =7$

$x= -1 \ \longrightarrow \ f(-1)=-2(-1)^2-8\cdot(-1)-1= 5$

$x= -3 \ \longrightarrow \ f(-3)=-2(-3)^2-8\cdot(-3)-1= 5$

$x= 0 \ \longrightarrow \ f(0)=-2\cdot0^2-8\cdot0-1= -1$

$x= -4 \ \longrightarrow \ f(-4)=-2(-4)^2-8\cdot(-4)-1= -1$

$\begin{array}{c|c} x & f(x) \\ \hline -2 & 7 \\ -1 & 5 \\ -3 & 5 \\ 0 & -1 \\ -4 & -1 \end{array}$

أخيرًا، نرسم النقاط على الرسم البياني ونرسم القطع المكافئ:

تمرين تم حله خطوة بخطوة للدالة التربيعية

التمرين 5

ارسم الدالة التربيعية غير الكاملة التالية على الرسم البياني:

$f(x)=x^2+2$

انظر الحل

إنها دالة متعددة الحدود من الدرجة الثانية. وبالتالي، لتمثيله، يجب عليك أولاً حساب الإحداثيات الإحداثية لرأس القطع المكافئ بالصيغة:

$x = \cfrac{-b}{2a} = \cfrac{-0}{2\cdot1} = \cfrac{0}{2} = 0$

في هذه الحالة تكون الدالة غير مكتملة، لأنها لا تحتوي على حد من الدرجة الأولى. من أجل هذا

$b=0 .$

الآن نصنع جدول القيم. للقيام بذلك، نحسب قيمة

$f(x)$

في الأعلى وحول الأعلى:

$x= 0 \ \longrightarrow \ f(0)=0^2+2=2$

$x= 1 \ \longrightarrow \ f(1)=1^2+2=3$

$x= -1 \ \longrightarrow \ f(-1)=(-1)^2+2=3$

$x= 2 \ \longrightarrow \ f(2)=2^2+2=6$

$x= -2 \ \longrightarrow \ f(-2)=(-2)^2+2=6$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 3 \\ -1 & 3 \\ 2 & 6 \\ -2 & 6 \end{array}$

أخيرًا، نرسم النقاط على الرسم البياني ونرسم القطع المكافئ:

تمارين محلولة لتمثيل دالة تربيعية غير مكتملة

التمرين 6

حل المسألة التالية المتعلقة بالدوال التربيعية:

يتم تحديد تكلفة إنتاج المنتج من خلال الوظيفة التالية:

$f(x)=x^2-12x+76$

ذهب

$x$

هي الوحدات المنتجة (بالآلاف) و

$f(x)$

هي تكلفة إنتاج الوحدات (بآلاف اليورو).

يمثل دالة تكلفة الإنتاج على الرسم البياني.
تحديد عدد آلاف الوحدات التي يجب إنتاجها لتقليل التكاليف.

انظر الحل

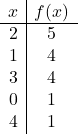
هذه دالة تربيعية. وبالتالي، لتمثيله، يجب عليك أولاً العثور على الإحداثيات الإحداثية لرأس القطع المكافئ بالصيغة:

$x = \cfrac{-b}{2a} = \cfrac{-(-12)}{2\cdot 1} = \cfrac{12}{2} = 6$

الآن نصنع جدول القيم. للقيام بذلك، نحسب قيمة

$f(x)$

في الأعلى وحول الأعلى:

$x= 6 \ \longrightarrow \ f(6)=6^2-12\cdot6+76 = 40$

$x= 5 \ \longrightarrow \ f(5)=5^2-12\cdot5+76 = 41$

$x= 7 \ \longrightarrow \ f(7)=7^2-12\cdot7+76 = 41$

$x= 4 \ \longrightarrow \ f(4)=4^2-12\cdot4+76 = 44$

$x= 8 \ \longrightarrow \ f(8)=8^2-12\cdot8+76 = 44$

$\begin{array}{c|c} x & f(x) \\ \hline 6 & 40 \\ 5 & 41 \\ 7 & 41 \\ 4 & 44 \\ 8 & 44 \end{array}$

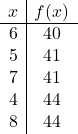
الآن نرسم النقاط على الرسم البياني ونرسم القطع المكافئ:

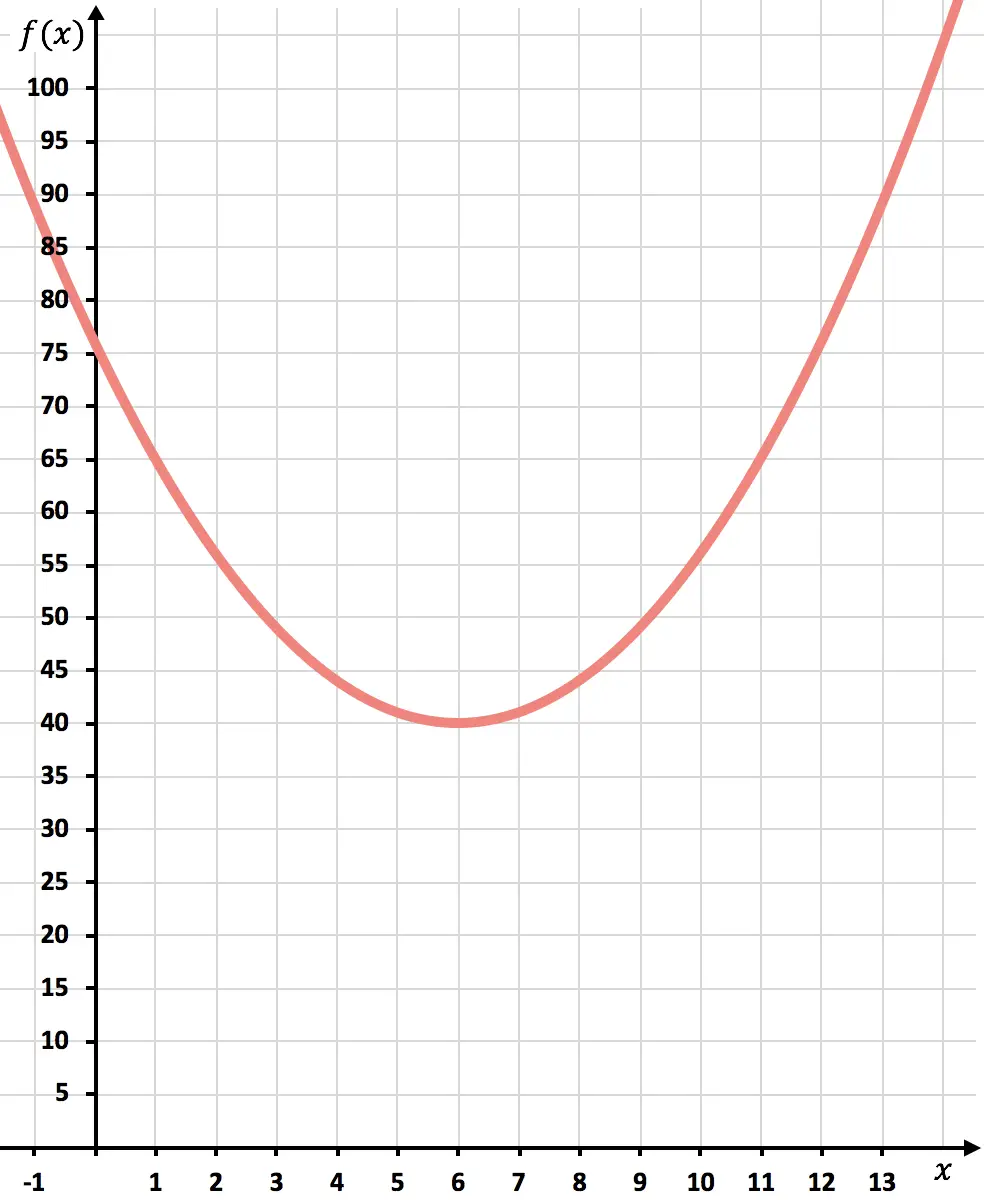
بمجرد تمثيل الوظيفة، سنرى مقدار التكاليف التي تم تقليلها.

وكما يوضح الرسم البياني، سيتم الوصول إلى الحد الأدنى من التكاليف في الجزء العلوي من القطع المكافئ. لأن هذا هو المكان الذي تأخذ فيه الوظيفة أصغر قيمة.

في الختام، سيتم تقليل التكاليف عن طريق إنتاج 6000 وحدة.

التمرين 7

حل مشكلة الدالة التربيعية التالية:

يؤدي الرياضي رمية الرمح التي يمكن تمثيل مسارها بالوظيفة التالية:

$h(x) = -0,025x^2+2x+2$

ذهب

$x$

هي الأمتار التي يغطيها الرمح و

$h$

ارتفاعه (أيضا بالأمتار).

ما هو أقصى ارتفاع يمكن أن يصل إليه الرمح؟

انظر الحل

هذه دالة تربيعية، لذا فإن مسار الرمح سيكون قطعًا مكافئًا.

بالإضافة إلى ذلك، بما أن معامل الحد التربيعي سالب (-0.025)، فإن القطع المكافئ سيكون له شكل U مقلوب وستتجه فروعه إلى الأسفل. وهكذا سيصل الرمح إلى أقصى ارتفاع في الأعلى، لأن هذه ستكون أعلى نقطة في القطع المكافئ.

لذلك نحسب حدود رأس القطع المكافئ بالصيغة:

$x = \cfrac{-b}{2a} = \cfrac{-2}{2\cdot (-0,025)} = \cfrac{-2}{-0,05} = 40$

وبعد ذلك نحسب مدى ارتفاع الرمح عند هذه النقطة من خلال تقييم الدالة

$x=40:$

$h(40) = -0,025\cdot (40)^2+2\cdot 40+2 = 42$

وبالتالي فإن الحد الأقصى للارتفاع الذي يمكن أن يصل إليه الرمح هو 42 مترًا.

التمرين 8

حل المسألة التالية المتعلقة بالدوال التربيعية:

يتم تحديد تكاليف الإنتاج (باليورو) للشركة من خلال الوظيفة التالية:

$C(q)=40000+20q+q^2$

ذهب

$q$

هي الوحدات المنتجة.

وسعر بيع كل وحدة هو 520 يورو.

ما مقدار الربح الذي ستحققه الشركة إذا باعت 150 وحدة؟
كم عدد الوحدات التي يجب بيعها لتحقيق أقصى ربح؟

انظر الحل

تكسب الشركة 520 يورو عن كل وحدة مباعة. وبالتالي فإن الدالة التي تحدد الدخل هي:

$I(q)=520\cdot q = 520q$

ذهب

$q$

هي الوحدات المباعة.

لكنهم يسألوننا عن الربح، أي الدخل مطروحًا منه التكاليف. لذلك نقوم بطرح الإيرادات مطروحًا منها التكاليف للحصول على الدالة التي تصف أرباح الشركة:

$B(q)=I(q)-C(q)$

$B(q)=520q - (40000+20q+q^2)$

$B(q)=520q - 40000-20q-q^2$

$B(q)=-q^2 + 500q - 40000$

بمجرد أن نعرف الدالة التي تصف أرباح الشركة، ما عليك سوى استبدال 150 في تعبير الدالة لحساب الربح الذي ستحصل عليه الشركة من خلال بيع 150 وحدة:

$\begin{aligned} B(150) & =-(150)^2 + 500\cdot 150 - 40000 \\[2ex] & = -22500+75000 - 40000 \\[2ex] & = \bm{12500} \end{aligned}$

لذلك، من خلال بيع 150 وحدة، ستحقق الشركة ربحًا قدره 12500 يورو.

يطلب منا البيان أيضًا حساب عدد الوحدات التي يتم تحقيق الحد الأقصى للربح فيها.

الدالة التي تصف الربح هي دالة تربيعية، لذا سيكون لها شكل القطع المكافئ. وبما أن معامل الحد التربيعي سالب (-1)، فإن القطع المكافئ سيكون له شكل U مقلوب وستتجه فروعه إلى الأسفل. لذلك، سيتم تحقيق الحد الأقصى من المكاسب في الأعلى، لأن هذه هي أعلى نقطة في القطع المكافئ.

لذلك نحسب حدود رأس القطع المكافئ بالصيغة:

$x = \cfrac{-b}{2a} = \cfrac{-500}{2\cdot(-1)} = \cfrac{-500}{-2} = 250$

وبالتالي ستحقق الشركة أقصى ربح من خلال بيع 250 وحدة.

من ناحية أخرى، حتى لو لم يطلب البيان الصحفي ذلك، يمكننا تحديد الربح الذي سيتم تحقيقه من خلال بيع هذه الوحدات الـ 250:

$B(250) =-(250)^2 + 500\cdot250- 40000= 22500$

€

دالة تربيعية أو قطع مكافئ

ما هي الدالة التربيعية؟

تقعر وتحدب الدالة التربيعية

قمة الدالة التربيعية

نقاط القطع مع محاور الدالة التربيعية

مثال لتمثيل دالة تربيعية أو مكافئة

تمارين محلولة على الدوال التربيعية

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

التمرين 6

التمرين 7

التمرين 8

اترك تعليقاً إلغاء الرد