وظيفة جيب التمام الزائدي

يوليو 4, 2023

ستجد هنا كل شيء عن دالة جيب التمام الزائدية: ما هي صيغتها، وتمثيلها الرسومي، وخصائصها، والعلاقات الرياضية مع الدوال الأخرى، وما إلى ذلك.

صيغة جيب التمام الزائدي

دالة جيب التمام الزائدية هي إحدى الدوال القطعية الرئيسية ويتم تمثيلها بالرمز cosh(x) . جيب التمام الزائدي يساوي مجموع e ^x زائد e ^-x مقسومًا على 2.

ولذلك، فإن صيغة جيب التمام الزائدي هي:

$\displaystyle\text{cosh}(x)=\cfrac{e^{x}+e^{-x}}{2}$

وبالتالي، فإن جيب التمام الزائدي يرتبط رياضيًا بالدالة الأسية. وفي الرابط التالي يمكنك الاطلاع على خصائص هذا النوع من الوظائف:

➤ انظر: خواص الدالة الأسية

تمثيل رسومي لجيب التمام الزائدي

التمثيل الرسومي لوظيفة جيب التمام الزائدي يكون في شكل دالة تربيعية (أو قطع مكافئ):

جيب التمام الزائدي

➤ انظر: التمثيل البياني للدالة التربيعية .

في هذا الرسم البياني، يمكننا أن نرى بوضوح أن جيب التمام الزائدي هو دالة زوجية، لأنه متماثل حول المحور y.

من ناحية أخرى، فإن الرسم البياني لجيب التمام الزائدي يختلف تمامًا عن رسم جيب التمام (الدالة المثلثية)، وهي دالة دورية. يمكنك مشاهدة التمثيل الرسومي لجيب التمام وجميع الاختلافات مع جيب التمام الزائدي في الرابط التالي:

➤ انظر: التمثيل الرسومي لوظيفة جيب التمام

خصائص جيب التمام الزائدي

جيب التمام الزائدي يحترم الخصائص التالية:

مجال دالة جيب التمام الزائدي هو جميع الأعداد الحقيقية:

$\text{Dom } f = \mathbb{R}$

بدلاً من ذلك، نطاق (أو مدى) دالة جيب التمام الزائدية هو 1 وكل الأرقام أكبر من 1:

$\text{Im } f= [1,+\infty)$

جيب التمام الزائدي هو وظيفة مستمرة وحتى.

$\displaystyle \text{cosh}(-x)=\text{cosh}(x)$

تتقاطع الدالة مع المحور Y عند النقطة x=0.

$(0,1)$

من ناحية أخرى، الدالة ليس لها نقطة تقاطع مع المحور X.

إن حدي اللانهاية (الموجب والسالب) لدالة جيب التمام الزائدية يعطيان ما لا نهاية.

$\displaystyle\lim_{x\to+\infty}\text{cosh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{cosh}(x)=+\infty$

يتناقص جيب التمام الزائدي حتى x = 0 ومن تلك النقطة يزداد إلى أجل غير مسمى، وبالتالي فإن الدالة لها حد أدنى عند x = 0.

$(0,1)$

الدالة محدبة في مجالها، لذلك ليس لها نقطة انعطاف.

مشتق دالة جيب التمام الزائدي هو جيب التمام الزائدي:

$f(x)=\text{cosh}(x) \ \longrightarrow \ f'(x)=\text{senh}(x)$

تكامل دالة جيب التمام الزائدي هو الجيب الزائدي:

$\displaystyle \int \text{cosh}(x) \ dx= \text{senh}(x) + C$

كثيرة حدود تايلور (أو سلسلة ماكلورين) لدالة جيب التمام الزائدية هي كما يلي:

$\displaystyle\text{cosh}(x)=1+\cfrac{x^2}{2!}+\cfrac{x^4}{4!}+\cfrac{x^6}{6!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n}}{(2n)!}$

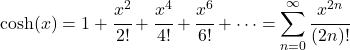
تحويل لابلاس لدالة جيب التمام الزائدية هو كما يلي:

$\mathcal{L}\bigl[\text{cosh}(at)\bigr]=\cfrac{s}{s^2-a^2}$

العلاقات الرياضية لجيب التمام الزائدي

بعد ذلك، سنرى كيف يمكن حساب جيب التمام الزائدي من دوال زائدية أخرى، حيث إنها كلها مرتبطة رياضيًا.

المعادلة الأساسية تربط جيب التمام الزائدي بالجيب الزائدي:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

➤ انظر: الجيب الزائدي

يمكن ربط الدوال الزائدية الثلاث الرئيسية (جيب التمام وجيب التمام والظل) بالمعادلة التالية:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

من ناحية أخرى، يمكن تحديد جيب التمام الزائدي للجمع (أو الطرح) لعددين مختلفين من خلال الصيغ التالية:

$\text{cosh}(x+y)=\text{cosh}(x)\text{cosh}(y)+\text{senh}(y)\text{senh}(x)$

$\text{cosh}(x-y)=\text{cosh}(x)\text{cosh}(y)-\text{senh}(y)\text{senh}(x)$

جيب التمام الزائدي لعدد مزدوج يساوي مجموع مربعات جيب التمام الزائدي وجيب التمام الزائدي لهذا الرقم:

$\text{cosh}(2x)=\text{cosh}^2(x)+\text{senh}^2(x)$

يمكن حساب جمع أو طرح جيب التمام الزائدي من خلال تطبيق الصيغ التالية:

$\displaystyle\text{cosh}(x)+\text{cosh}(y)=2\text{cosh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{cosh}(x)-\text{cosh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{senh}\left(\frac{x-y}{2}\right)$

وأخيرًا، يمكن حساب مربع جيب التمام الزائدي بالصيغة التالية:

$\text{cosh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)+1\Bigr)$

اترك تعليقاً إلغاء الرد