▷ تقعر وتحدب الدالة (الانحناء)

هنا سوف تتعلم ما هو التقعر والتحدب للدالة وكيفية معرفة ما إذا كانت الوظيفة مقعرة أو محدبة. بالإضافة إلى ذلك، سوف تكون قادرًا على التدرب من خلال تمارين خطوة بخطوة على انحناء الوظيفة.

ما هو تقعر وتحدب الوظيفة؟

يشير تقعر وتحدب الدالة إلى انحناء الرسم البياني للدالة. الدالة المقعرة هي دالة رسمها البياني على شكل جبل، والدالة المحدبة هي دالة رسمها البياني على شكل وادي.

في الفقرة السابقة تم تعريف الدوال المقعرة والدوال المحدبة بشكل غير رسمي لسهولة الفهم، ولكن التعريف الرياضي للدالة المقعرة والدالة المحدبة هو كما يلي:

الدالة المقعرة: عندما تكون القطعة التي تصل أي نقطتين من الدالة أسفل المنحنى.
دالة محدبة: عندما تكون القطعة التي تصل أي نقطتين من الدالة أعلى المنحنى.

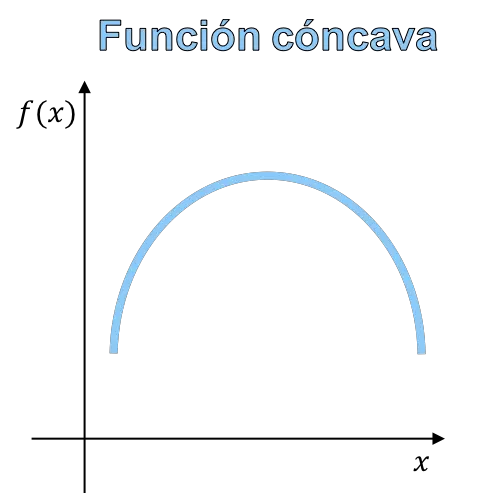
في النهاية، الفرق بين الدالة المقعرة والدالة المحدبة يكمن في شكل الدالة، وبالتالي، يمكنك التمييز بين التقعر والتحدب من الرسم البياني للدالة.

ومع ذلك، ليس من الضروري أن تكون الدالة مقعرة أو محدبة على مجالها بأكمله، ولكن يمكن أيضًا أن تكون مقعرة خلال فترة واحدة ومحدبة خلال فترة أخرى.

ملاحظة: لا يزال المجتمع الرياضي غير موافق تمامًا، ولذلك يقول بعض الأساتذة عكس ذلك: فهم يسمون الدالة المقعرة التي لها شكل

$\bm{\cup}$

، والدالة المحدبة التي لها شكل

$\bm{\cap}$

. وفي كل الأحوال، المهم هو معرفة ما هي الوظيفة، مهما كان اسمها.

كيفية دراسة انحناء الوظيفة

تتضمن دراسة انحناء الدالة إيجاد تقعر وتحدب الدالة، أي معرفة الفترات التي تكون فيها الدالة مقعرة والفترات التي تكون فيها الدالة محدبة.

لذا، لدراسة انحناء دالة، يجب تنفيذ الخطوات التالية:

أوجد النقاط التي لا تنتمي إلى مجال الدالة .
احسب المشتقة الأولى والمشتقة الثانية للدالة.
أوجد جذور المشتقة الثانية ، أي احسب النقاط التي تلغي المشتقة الثانية بالحل
$f''(x)=0$

.
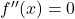
قم بعمل فترات زمنية مع جذور المشتقة والنقاط التي لا تنتمي إلى مجال الدالة.
احسب قيمة المشتقة الثانية عند نقطة في كل فترة.
وبالتالي فإن إشارة المشتقة الثانية تحدد تقعر أو تحدب الدالة في هذه الفترة:
- إذا كانت المشتقة الثانية للدالة موجبة، تكون الدالة محدبة في هذه الفترة.
- إذا كانت المشتقة الثانية للدالة سالبة، تكون الدالة مقعرة في هذه الفترة.

مثال على كيفية العثور على انحناء دالة

بعد ذلك، سنحل مثالًا خطوة بخطوة حتى تتمكن من رؤية كيفية حساب فترات التقعر والتحدب للدالة.

دراسة تقعر وتحدب الدالة التالية:

$f(x)=x^3-3x$

أول شيء يجب فعله هو حساب مجال تعريف الدالة. في هذه الحالة، لدينا دالة متعددة الحدود، وبالتالي فإن مجال الدالة يتكون من أعداد حقيقية:

$\text{Dom } f= \mathbb{R}$

بمجرد أن نحسب مجال الدالة، علينا التحقق من النقاط التي تختفي عندها المشتقة الثانية للدالة.

لذلك نحسب المشتقة الأولى للدالة:

$f(x)=x^3-3x \ \longrightarrow \ f'(x)= 3x^2-3$

ثم نجد المشتقة الثانية للدالة:

$f'(x)=3x^2-3 \ \longrightarrow \ f''(x)= 6x$

والآن نجعل المشتقة الثانية تساوي 0 ونحل المعادلة:

$f''(x)=0$

$6x=0$

$x=\cfrac{0}{6}$

$x=0$

بمجرد أن نحسب مجال الوظيفة و

$f''(x)=0$

، فإننا نمثل جميع النقاط الحرجة الموجودة على الخط. في هذه الحالة لم نجد أي نقطة حرجة في حساب مجال تعريف الدالة، لكننا حصلنا على نقطة تلغي المشتقة الثانية للدالة:

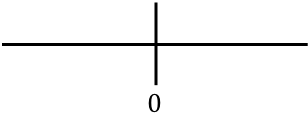
والآن نحسب إشارة المشتقة الثانية في كل فترة لنعرف ما إذا كانت الدالة مقعرة أم محدبة. لذلك نأخذ نقطة في كل فترة (وليس النقاط الحرجة أبدًا) وننظر إلى الإشارة التي يحملها المشتق الثاني عند هذه النقطة:

$f''(x)=6x$

$f''(-1) = 6\cdot (-1)=-6 \ \rightarrow \ \bm{-}$

$f''(1) = 6\cdot 1=+6 \ \rightarrow \ \bm{+}$

وأخيرًا، نستنتج فترات التقعر والتحدب للدالة. إذا كانت المشتقة الثانية موجبة، فهذا يعني أن الدالة محدبة.

$(\bm{\cup})$

وإذا كانت المشتقة الثانية سالبة فهذا يعني أن الدالة مقعرة

$(\bm{\cap})$

. وبالتالي فإن فترات التقعر والتحدب للوظيفة هي:

محدب

$(\bm{\cup})$

$\bm{(0,+\infty)}$

مقعر

$(\bm{\cap})$

$\bm{(-\infty,0)}$

تمارين محلولة على تقعر وتحدب الدالة

التمرين 1

احسب فترات التقعر والتحدب للدالة متعددة الحدود التالية:

$f(x) = x^3-3x^2-2x$

انظر الحل

الدالة في التمرين هي كثيرة الحدود، وبالتالي فإن مجال الدالة يتكون من أرقام حقيقية:

$\text{Dom } f= \mathbb{R}$

بعد تحديد مجال الدالة نفرقها:

$f(x)=x^3-3x^2-2x \ \longrightarrow \ f'(x)= 3x^2-6x-2$

ثم نجد المشتقة الثانية للدالة:

$f'(x)= 3x^2-6x-2 \ \longrightarrow \ f''(x)= 6x-6$

والآن نجعل المشتقة الثانية تساوي 0 ونحل المعادلة:

$f''(x)= 0$

$6x-6= 0$

$6x= 6$

$x= \cfrac{6}{6}$

$x=1$

بمجرد أن نحسب مجال الوظيفة ونحلها

$f''(x)=0$

، فإننا نمثل جميع النقاط المفردة الموجودة على خط الأعداد:

والآن لنأخذ نقطة تنتمي إلى كل فترة ونرى ما هي الإشارة التي تحتوي على المشتقة الثانية عند هذه النقطة:

$f''(0)= 6\cdot 0-6 = -6 \ \rightarrow \ \bm{-}$

$f''(2)= 6\cdot 2-6 = 12-6=+6 \ \rightarrow \ \bm{+}$

عندما تكون المشتقة الثانية أكبر من الصفر، فهذا يعني أن الدالة محدبة.

$(\bm{\cup})$

لكن عندما تكون المشتقة الثانية سالبة فهذا يعني أن الدالة مقعرة

$(\bm{\cap})$

. وبالتالي فإن فترات التقعر والتحدب هي:

محدب

$(\bm{\cup})$

$\bm{(1,+\infty)}$

مقعر

$(\bm{\cap})$

$\bm{(-\infty,1)}$

تمرين 2

ادرس انحناء الدالة العقلانية التالية:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

انظر الحل

نحتاج أولاً إلى حساب مجال الوظيفة. وبما أن هذه دالة كسرية، فقد جعلنا المقام يساوي الصفر لمعرفة الأرقام التي لا تنتمي إلى مجال الدالة:

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

هذا يعني أنه عندما تكون x -2 أو +2، فإن المقام سيكون 0. وبالتالي، لن تكون الدالة موجودة. وبالتالي فإن مجال الدالة يتكون من جميع الأرقام باستثناء x=-2 وx=+2.

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

ثانياً، نحسب المشتقة الأولى للدالة:

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

ثم نحل المشتقة الثانية:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

يتم ضرب جميع المصطلحات بـ

$(x^2-4)$

. يمكننا بالتالي تبسيط الكسر:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

الآن دعونا نحسب جذور المشتق الثاني للدالة:

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

على المدى

$\left(x^2-4\right)^3$

يتضمن ذلك تقسيم الجانب الأيسر بأكمله، حتى نتمكن من ضربه في الجانب الأيمن بأكمله:

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

نستخرج العامل المشترك :

$x(8x^2+96)=0$

لكي يكون الضرب يساوي 0، يجب أن يكون أحد عنصري الضرب صفراً. ولذلك، فإننا نجعل كل عامل يساوي 0:

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$

لا يوجد حل لأنه لا يوجد جذر سلبي لعدد حقيقي.

نمثل الآن على الخط جميع النقاط الحرجة التي تم الحصول عليها، أي النقاط التي لا تنتمي إلى المجال (x=-2 وx=+2) وتلك التي تلغي المشتقة الثانية (x=0):

ونحسب إشارة المشتقة الثانية في كل فترة لنعرف ما إذا كانت الدالة مقعرة أم محدبة. لذلك نأخذ نقطة في كل فترة وننظر إلى الإشارة التي تحتوي على المشتقة الثانية عند تلك النقطة:

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

إذا كانت المشتقة الثانية موجبة، فهذا يعني أن الدالة محدبة.

$(\bm{\cup})$

وإذا كانت المشتقة الثانية سالبة فهذا يعني أن الدالة مقعرة

$(\bm{\cap})$

. وبالتالي فإن فترات التقعر والتحدب هي:

محدب

$(\bm{\cup})$

$\bm{(-2,0)\cup (2,+\infty)}$

مقعر

$(\bm{\cap})$

$\bm{(-\infty,-2)\cup (0,2)}$

التمرين 3

وظيفة

$f(x)$

لديه تطرف نسبي في

$x=3$

. والأكثر من ذلك، أن الوظيفة محدبة

$(\cup )$

في هذه النقطة نفسها. تحديد ما إذا كان الحد الأقصى النسبي هو الحد الأدنى أو الحد الأقصى.

➤ انظر: تعريف الحد الأقصى والحد الأدنى للدالة

انظر الحل

دع الوظيفة المحدبة

$(\cup)$

في

$x=3$

يعني أن المشتقة الثانية عند هذه النقطة موجبة، أي

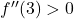$f''(3)>0″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”74″ style=”vertical-align: -5px;”></p> <p> .</p> <p class=$ ولذلك، فإن المتطرفة النسبية لل

$\bm{x=3}$

وهذا هو الحد الأدنى ، منذ ذلك الحين

$f''(3)$

انها إيجابية.

ما هو تقعر وتحدب الوظيفة؟

كيفية دراسة انحناء الوظيفة

مثال على كيفية العثور على انحناء دالة

تمارين محلولة على تقعر وتحدب الدالة

التمرين 1

تمرين 2

التمرين 3

اترك تعليقاً إلغاء الرد