وظائف محدودة

نوضح في هذه المقالة ماهية الدوال المحددة (العلوية والسفلى). بالإضافة إلى ذلك، سنوضح لك ما يعنيه أن تكون الدالة محددة عند نقطة ما، وأخيرًا، ستجد خصائص هذا النوع من الدوال.

ما هي الدالة المحدودة؟

الدالة المقيدة هي دالة يكون رسمها البياني ضمن الحدود. أي أن الدالة تكون محدودة من الأعلى إذا كان هناك رقم K بحيث لا توجد قيمة للدالة أكبر من K (f(x)≥K)، وتكون الدالة محدودة من الأسفل إذا كان هناك رقم K بحيث تكون أقل من جميع قيم الدالة (f(x)≥K). وبالتالي، فإن الدالة المحددة هي دالة محدودة من الأعلى والأسفل.

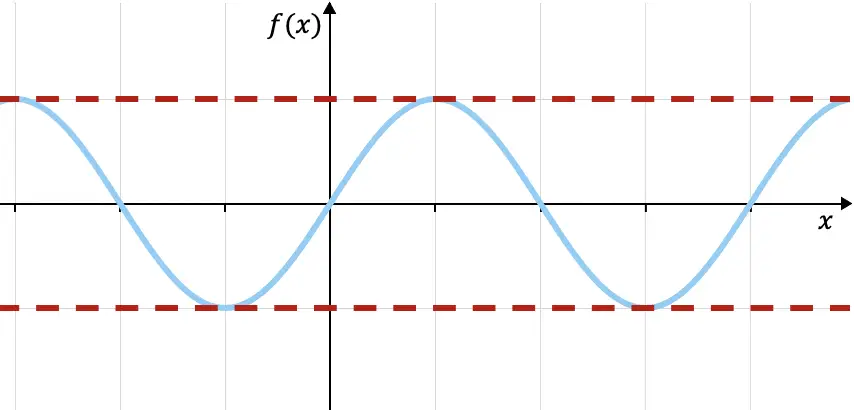
على سبيل المثال، دالة الجيب المثلثية، الموضحة أعلاه، يحدها من الأعلى f(x)=1 ويحدها من الأسفل f(x)=-1 (خطوط منقطة حمراء)، لأن جميع قيم الدالة الوظيفة ضمن هذين الحدين. يمكنك رؤية المزيد من خصائص هذه الوظيفة في الرابط التالي:

➤ انظر:خصائص دالة الجيب

وظيفة يحدها أعلاه

ومع ذلك، ليست كل الدوال محددة من الأعلى والأسفل، يمكن أن تكون الدالة محدودة فقط من الأعلى أو الأسفل.

الوظائف المحددة أعلاه هي تلك التي لا تتجاوز قيمة معينة، أي يتم استيفاء الشرط التالي:

$f(x)\leq K$

حيث القيمة K هي الحد الأعلى للدالة.

على سبيل المثال، القطع المكافئ التالي محدد من الأعلى بـ K=7، لكن الدالة غير محدودة من الأسفل لأن فروعها تمتد إلى ما لا نهاية.

منطقيًا، إذا كانت الدالة محدودة بـ K=7، فإنها تكون أيضًا محدودة بـ K=8 والقيم الأعلى.

يُطلق على الحد الأعلى الأصغر اسم الحد العلوي ويتم تمثيله بـ su(f) . علاوة على ذلك، إذا وصلت الدالة إلى الحد الأعلى المذكور في مجالها، فسنقول إن هذه النقطة هي الحد الأقصى المطلق للدالة.

➤ انظر: ما هو الحد الأقصى والحد الأدنى للدالة؟

في حالتنا، تكون الدالة محدودة هندسيًا بـ K=7، وبالتالي فهي الحد الأعلى والحد الأقصى المطلق للدالة.

وظيفة محددة أدناه

الوظائف المحددة أدناه هي تلك التي ليس لها قيمة أقل من رقم معين، أي أنها تلبي التعبير الرياضي التالي:

$f(x)\geq K$

حيث تكون قيمة K هي الحد الأدنى للدالة.

يوجد أدناه تمثيل رسومي للدالة الأسية المحددة أدناه بـ K=3:

من الواضح أن الدالة محدودة أيضًا بقيم أقل من K=3.

كما كان من قبل، الحد الأدنى الأكبر يسمى الحد الأدنى ويمثله inf(f) . علاوة على ذلك، إذا وصلت الدالة إلى الحد الأدنى المذكور في مجالها، فسنقول أن هذه النقطة هي الحد الأدنى المطلق للدالة.

في هذه الحالة، K=3 ليس الحد الأدنى المطلق للدالة، لأن الدالة تصل إلى هذه القيمة عند اللانهاية، وبالتالي فهي خارج مجالها. بمعنى آخر، f(x)=3 هو خط مقارب أفقي للدالة .

هناك نظرية تسمح لك بمعرفة ما إذا كانت الدالة محددة من الأعلى والأسفل دون تمثيلها الرسومي. انقر هنا لمعرفة ما هي نظرية Weierstrass.

➤ انظر: نظرية فايرستراس

الدالة محددة عند نقطة واحدة

لقد درسنا للتو فكرة تقييد الدالة بشكل عام، ولكن من الممكن أيضًا تحليل ما إذا كانت الدالة محصورة في منطقة أصغر أم لا، أي في جزء من الدالة.

نعم

$a$

هي نقطة في مجال الوظيفة و

$r$

أي قيمة، سنقول أن الدالة محدودة من الأعلى/الأسفل عند هذه النقطة

$a$

إذا كانت هناك بيئة

$V(a,r)$

حيث يحدها الدالة أعلى/أسفل.

ولذلك، فإن الدالة محدودة عند هذه النقطة

$a$

إذا كان محددًا من الأعلى والأسفل في الحي

$V(a,r).$

من الواضح أنه إذا كانت الدالة محددة بشكل عام، فستكون أيضًا محدودة عند كل نقطة من نقاطها. ومع ذلك، فإن العكس غير صحيح، أي أن الدالة يمكن أن تكون محدودة في كل نقطة من نقاطها ولا تكون محدودة في مجالها بأكمله.

على سبيل المثال، تكون الدالة التقريبية التالية محدودة جزئيًا عند كل نقطة من نقاطها، ولكنها ليست دالة محدودة.

خصائص الدوال المحدودة

الوظائف المحددة لها الخصائص التالية:

نعم
$f(x)$

و

$g(x)$

هما دالتان محدودتان، جمع (أو طرح) الدالتين

$f(x)\pm g(x)$

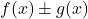
هي أيضًا دالة محدودة.
نعم
$f(x)$

و

$g(x)$

هما دالتان محدودتان، حاصل ضرب الدالتين

$f(x)\cdot g(x)$

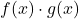
يحدث أيضًا أن تكون دالة محدودة.
إذا كانت الدالة تحتوي على خط تقارب رأسي، فلا يمكن أن تكون محددة تمامًا. من ناحية أخرى، يمكن أن تكون الدالة محدودة للأعلى أو للأسفل.
أي دالة متصلة ومحدودة على فترة تكون قابلة للتكامل.