ستجد في هذه المقالة شرحًا تفصيليًا للغاية حول الدوال متعددة الحدود ، مكملاً بالأمثلة. بالإضافة إلى ذلك، ستتمكن من رؤية كيفية استخدام الدوال متعددة الحدود في الحياة اليومية بفضل التمارين التي سنقدمها لك في النهاية.
ما هي وظيفة متعددة الحدود؟
الدوال كثيرة الحدود أو الدوال متعددة الحدود هي دوال تُعطى بواسطة تعبير جبري مكافئ لكثيرة الحدود . هذا يعني أن التعبير يجب أن يتبع بنية كثيرة الحدود: f(x) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + … + a n x n ، اعتمادًا على بنيتها التي سنذكرها تحديد نوع دالة متعددة الحدود التي سنقوم بمعالجتها. خاصية أخرى ذات صلة جدًا بهذه الوظائف هي أن جميع أسس المجهولة الخاصة بها هي أعداد موجبة وأعداد صحيحة .
أجزاء من وظيفة كثيرة الحدود
ويمكننا تسليط الضوء على ثلاثة عناصر مهمة فيما يتعلق بهذه الوظائف:
- معاملات كثيرة الحدود: وهي الأعداد التي تصاحب المجهولات، مثلاً 3 من الحد التالي هو معامل: 3x 2 . تجدر الإشارة إلى أن عدد المعاملات يساوي عدد الحدود في كثيرة الحدود.
- أسس أو فهارس كثيرة الحدود: وهي قوى المجهول، على سبيل المثال 2 للمصطلح التالي هو أس: 3x 2 . وكما أوضحنا سابقًا، في حالة الدالة كثيرة الحدود، ستكون دائمًا موجبة وعددًا صحيحًا.
- درجة كثيرة الحدود: هذه القيمة تعادل أس أعلى درجة بين جميع الحدود التي تشكل كثيرة الحدود. في حالة كثيرة الحدود f(x) = 3x 2 – 4x + 2، الدرجة تساوي اثنين.
كيف يمكنك معرفة ما إذا كانت الدالة متعددة الحدود أم لا؟
لتحديد دالة متعددة الحدود، يجب أن ننظر لمعرفة ما إذا كانت تلبي الخصائص التي تحدثنا عنها للتو. سنبدأ بالتحقق مما إذا كان التعبير الذي يحدد الدالة له بنية متعددة الحدود : f(x) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + … + a n x n . وبعد ذلك، سوف نتحقق من أن الأرقام موجبة وعدد صحيح، وبهذه الخطوات البسيطة سنتمكن من تحديد ما إذا كانت الدالة كثيرة الحدود أم لا.
أنواع الدوال كثيرة الحدود مع الأمثلة
بعد ذلك، سنعرض لك الأنواع المختلفة من الدوال كثيرة الحدود الموجودة، والتي يتم تصنيفها وفقًا لدرجة كثيرة الحدود. بالإضافة إلى ذلك، سوف تجد مثالاً لتمثيل رسومي لكل نوع. بفضل هذه الأمثلة للدوال متعددة الحدود، ستتمكن من رؤية الاختلافات بين الفئات المختلفة بشكل أفضل.
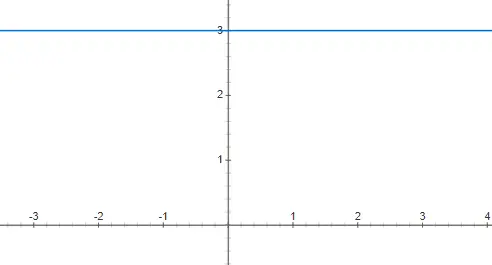
وظائف ثابتة
الدوال الثابتة تعادل متعددة الحدود من الدرجة 0، وهذا يعني أن معامل x هو 0. ولهذا السبب لا تعتمد الدوال من هذا النوع على قيمة المتغير المستقل x. ولذلك، فإن تمثيله الرسومي هو خط أفقي، وهو لانهائي. يمكنك العثور أدناه على المثال f(x) = 3 ممثلًا:
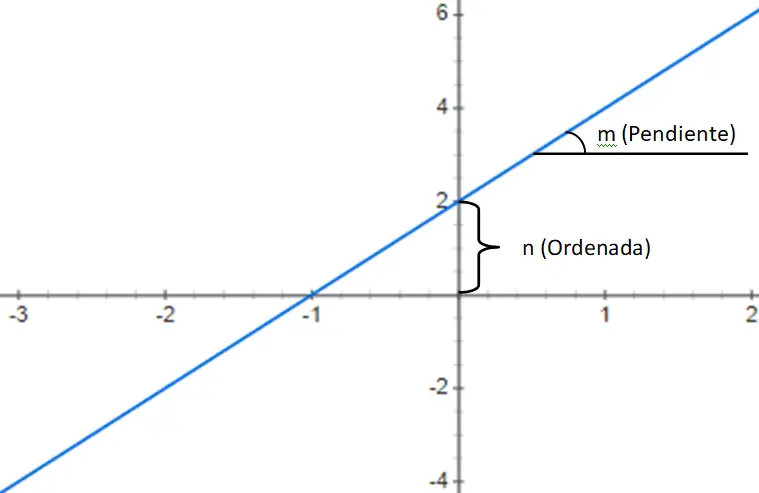
وظائف متعددة الحدود من الدرجة الأولى
ثانيًا، نجد دوال متعددة الحدود من الدرجة الأولى ، والتي تُعطى بواسطة متعددة الحدود من الدرجة 1 بالبنية التالية: f(x) = mx + n. يتكون هذا التعبير من رقم يسمى الميل (m) الذي يضرب المتغير xy بالثابت (n) الذي يضاف إلى هذا المنتج. لذا، بناءً على قيمتي m وn، يمكننا تحديد ثلاثة أنواع مختلفة من الوظائف:
- الدالات الأفينية: يتميز هذا النوع الفرعي بوجود قيمة n تختلف عن 0، أي أن قيمة الكمبيوتر تختلف عن 0. ولذلك فإن هذا النوع من الوظائف لا يمر عبر النقطة (0، 0)، وتسمى أيضًا الأصل. علق أيضًا أنه إذا كانت m <0، فستتناقص الدالة، بينما إذا كانت m > 0، فستزداد الدالة.
- الدوال الخطية: الفرق الوحيد بين هذه الدوال والدوال المتقاربة هو أن n = 0، لذلك ليس لديهم جهاز كمبيوتر. ولذلك، فإن التعبير عن الدوال الخطية يعادل f(x) = mx. من السهل جدًا تمثيل هذا النوع، لأنه يمر دائمًا بالنقطة (0، 0) ومن المنحدر نحصل بالفعل على الرسم البياني.
- دوال الهوية: هذا النوع الأخير عبارة عن مجموعة فرعية من الدوال الخطية، والتي an = 0 و m = 1. وهذا يعني أن التعبير يظل f(x) = x، حيث يكون التمثيل الرسومي قطريًا يشكل زاوية 45 درجة مع أحد المحاور. ويمر هذا النوع من الوظائف أيضًا عبر نقطة الأصل (0، 0).
ستجد أدناه مثالاً لدالة متعددة الحدود من الدرجة الأولى، وبشكل أكثر دقة، دالة تقاربية f(x) = 3x + 2:
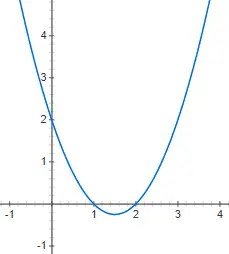
وظائف تربيعية
يتم التعبير عن الدوال التربيعية أو الدوال التربيعية باستخدام متعددات الحدود التربيعية، والتي تتبع البنية: f(x) = ax 2 + bx + c، حيث يختلف a عن 0. في هذه الحالة، يكون التمثيل الرسومي أكثر تعقيدًا، لأنه لم يعد خطًا مستقيمًا، بل قطعًا مكافئًا عموديًا . يمكنك العثور أدناه على تمثيل الدالة التربيعية f(x) = 2x 2 + 4x – 1:
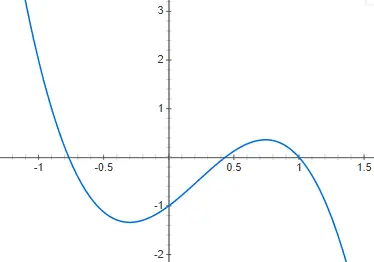
وظائف مكعب
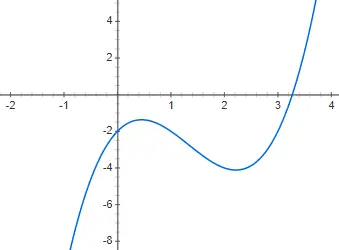
تُعطى الدوال التكعيبية أو الدوال من الدرجة الثالثة بواسطة متعددة الحدود من الدرجة الثالثة: f(x) = ax 3 + bx 2 + cx + d، كونها مختلفة عن 0. تمثيل دالة من هذا النمط أكثر تعقيدًا من من الدرجة الثانية، لأنه يمكن أن يكون له عدة أشكال مختلفة. على الرغم من أن الصيغة الأساسية، أو على الأقل الأكثر شيوعًا، هي التي سنعرضها لك في المثال التالي، f(x) = 2x 3 – 4x 2 + 2x – 2:
خصائص وظائف متعددة الحدود
الدوال كثيرة الحدود لها سلسلة من الخصائص أو الخصائص التي تميزها عن غيرها من الدوال، وسنقوم بتفصيلها بأكبر قدر ممكن من التفصيل أدناه. بهذه الطريقة، عندما ترى وظائف مثل هذه، سيكون من السهل جدًا عليك التعرف عليها:
- مجال الدالة كثيرة الحدود يساوي جميع الأعداد الحقيقية : Dom f = R أو Dom f = (-∞, ∞)، وبالتالي فهي متصلة على مجموعة الأعداد الحقيقية بأكملها.
- نقطة تقاطعها على المحور Y تعادل (0, a 0 )، 0 هو الحد المستقل.
- يقطع على طول المحور X عدة مرات يساوي أو يقل عن درجة كثير الحدود.
- الدوال كثيرة الحدود لا تحتوي على خطوط مقاربة.
- إذا كان أس جميع الحدود فرديًا، فإن الرسم البياني يكون متماثلًا حول أصل الإحداثيات، بينما إذا كان أس جميع الحدود زوجيًا، فهو متماثل حول محور OY.
- عدد نقاط انعطاف دالة من هذا النمط يساوي أو أقل من n – 2، حيث n هي الدرجة.
- عدد الحدود القصوى والصغرى النسبية لدالة هذا النمط يساوي أو أقل من n – 1، حيث n هي الدرجة.
كيف يمكنك تحليل وظيفة متعددة الحدود؟
لتحليل دالة كثيرة الحدود، يجب أن نتبع نفس الإجراء الذي نستخدمه لتحليل أي دالة أخرى. وفي القائمة التالية قمنا بتلخيص العناصر المختلفة التي يجب دراستها أو معالجتها:
- المجال والمدى
- نقاط التقاطع مع المحورين الأفقي والرأسي
- الرتابة (الزيادة والنقصان، الحد الأقصى والحد الأدنى)
- الانحناء (في وظائف درجة أكبر من واحد)
ومن الواضح أنه يمكننا أن نأخذ التحليل إلى مستوى آخر وندرس العديد من العناصر الأخرى، على الرغم من أن هذا ينبغي أن يكون كافيا. نظرًا لأنه بمعرفة هذه العناصر، سيكون لديك فكرة واضحة عن شكل الوظيفة وستكون قادرًا على تمثيلها بيانيًا.
تمارين على وظائف متعددة الحدود
بعد ذلك، نقدم لك سلسلة من التمارين للتدرب على تمثيل الدوال ، وخاصة الدوال متعددة الحدود. بهذه الطريقة سوف تقوم بدمج جميع المفاهيم الموضحة في هذه المقالة:
التمرين 1
ارسم دالة متعددة الحدود من الدرجة الأولى التالية f(x) = x + 2 وحدد نوعها:
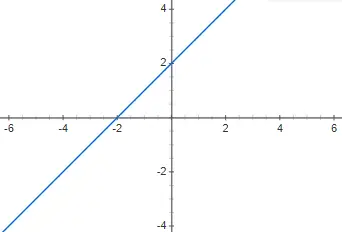
إنها دالة متعددة الحدود من الدرجة الأولى، لأنها تختلف عن 0 وm تختلف عن 0.
تمرين 2
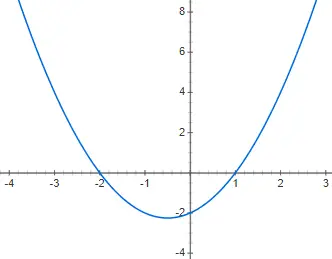
ارسم بيانيًا الدالة متعددة الحدود التربيعية التالية f(x) = x 2 + x – 2:
التمرين 3
ارسم بيانيًا دالة متعددة الحدود من الدرجة الثالثة التالية f(x) = x 2 + x – 2: