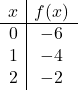وظائف القيمة المطلقة

سبتمبر 17, 2023

تشرح هذه الصفحة ماهية دالة القيمة المطلقة. سوف تتعلم أيضًا كيفية تحديد دالة القيمة المطلقة متعددة التعريف وكيفية تمثيل هذه الأنواع من الوظائف على الرسم البياني. بالإضافة إلى ذلك، ستشاهد ذلك مع أمثلة لدوال القيمة المطلقة وستكون قادرًا على التدرب على التمارين والمسائل التي تم حلها خطوة بخطوة.

ما هي وظائف القيمة المطلقة؟

تعريف دالة القيمة المطلقة هو كما يلي:

القيمة المطلقة للدالة تحول جميع صورها إلى صور إيجابية. ولذلك، فإن مسار الدالة المطلقة لا يمكن أن يكون له قيم سالبة أبدًا.

الدالة التالية هي مثال لدالة القيمة المطلقة:

$f(x)=\lvert 5x \rvert$

إذا حصلنا عند تقييم الدالة عند نقطة ما على نتيجة إيجابية، فإنها تظل إيجابية:

$f(1)=\lvert 5\cdot 1 \rvert =\lvert 5 \rvert = 5$

ومن ناحية أخرى، إذا كانت النتيجة سلبية تصبح إيجابية:

$f(-1)=\lvert 5\cdot (-1) \rvert =\lvert -5 \rvert = 5$

عادة ما يتم إعطاء دوال القيمة المطلقة في المدرسة الثانوية، لأن خصائصها تجعل فهمها صعبًا بعض الشيء.

كيفية تعريف دالة متعددة القيمة ذات قيمة مطلقة

يمكن التعبير عن دالة القيمة المطلقة كدالة متعددة التعريف. للقيام بذلك، عليك تغيير إشارة الدالة على الفترات التي تكون سالبة.

دعونا نرى مثالاً لكيفية الانتقال من دالة القيمة المطلقة إلى دالة متعددة التعريف:

عبر عن الدالة التالية بقيمة مطلقة في صورة دالة متعددة التعريف:

$f(x) = \lvert 4 - x^2 \rvert$

أول ما علينا فعله هو تحديد متى تكون الدالة سالبة. للقيام بذلك، قمنا بتعيين التعبير الجبري بقيمة مطلقة تساوي 0 وحل المعادلة:

$4-x^2=0$

$4 = x^2$

$\sqrt{4}=\sqrt{x^2}$

$\pm 2 = x$

$x=+2 \qquad x=-2$

نحن الآن نمثل القيم التي تم الحصول عليها على السطر:

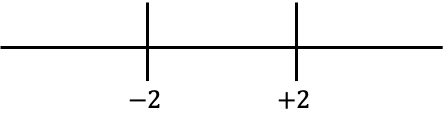
وننظر إلى العلامة التي لها الدالة بدون القيمة المطلقة في كل فترة من الخط:

$x<-2$

نأخذ أي نقطة أقل من -2، على سبيل المثال

$x=-3:$

$4-(-3)^2$

$-5$

سلبي

$-2 < x < 2$

نأخذ أي نقطة بين -2 و+2، على سبيل المثال

$x=0:$

$4-0^2$

$+4$

إيجابي

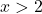$x>2″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”42″ style=”vertical-align: -2px;”> <p style=$ على سبيل المثال، نأخذ أي نقطة أكبر من 2

$x=3:$

$4-3^2$

$-5$

سلبي

وكما رأينا، فإن الدالة بدون القيمة المطلقة ستكون سالبة على الفترات

$x<-2$

$x>2.” title=”Rendered by QuickLaTeX.com” height=”14″ width=”47″ style=”vertical-align: -2px;”> لذلك، نحتاج إلى التعبير عن الدالة بشرطات عن طريق تغيير علامتها في هذه الفترات: <p style=$

$\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -(4-x^2) & \text{si} & x<-2 \\[2ex] 4-x^2 & \text{si} & -2 \le x \le 2 \\[2ex] -(4-x^2) & \text{si} & x>2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”372″ style=”vertical-align: 0px;”> <p style=$

$\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x<-2 \\[2ex] 4-x^2 & \text{si} & -2 \le x \le 2 \\[2ex] -4+x^2 & \text{si} & x>2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”358″ style=”vertical-align: 0px;”> <p style=$ لاحظ أنه في بعض الفواصل الزمنية يجب عليك تضمين المساواة. على سبيل المثال، هنا نضعها في الفترة الثانية

$-2 \le x \le 2$

. لكن يمكنك وضعها في أي فترة زمنية تريدها طالما أن هناك تعادلًا في جميع النقاط الحرجة. بمعنى آخر، سيكون الأمر نفسه لو عرفنا الدالة على النحو التالي:

$\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x\le-2 \\[2ex] 4-x^2 & \text{si} & -2 < x < 2 \\[2ex] -4+x^2 & \text{si} & x\ge 2 \end{array} \right.$

كيفية تمثيل دالة بقيمة مطلقة

لتمثيل دالة ذات قيمة مطلقة على الرسم البياني، نحتاج إلى اتباع الخطوات الموضحة أدناه:

قم بتمثيل الدالة كما لو لم يكن لها قيمة مطلقة.
في الفترات التي تكون فيها الدالة سالبة، أي أنها تقع أسفل المحور X، ارسم الدالة المتماثلة.
احذف جزء الدالة الموجود أسفل المحور X.

دعونا نرى مثالاً لكيفية رسم دالة بيانيًا بقيمة مطلقة

قم برسم الدالة التالية بالقيمة المطلقة:

$f(x) = \lvert -x+2 \rvert$

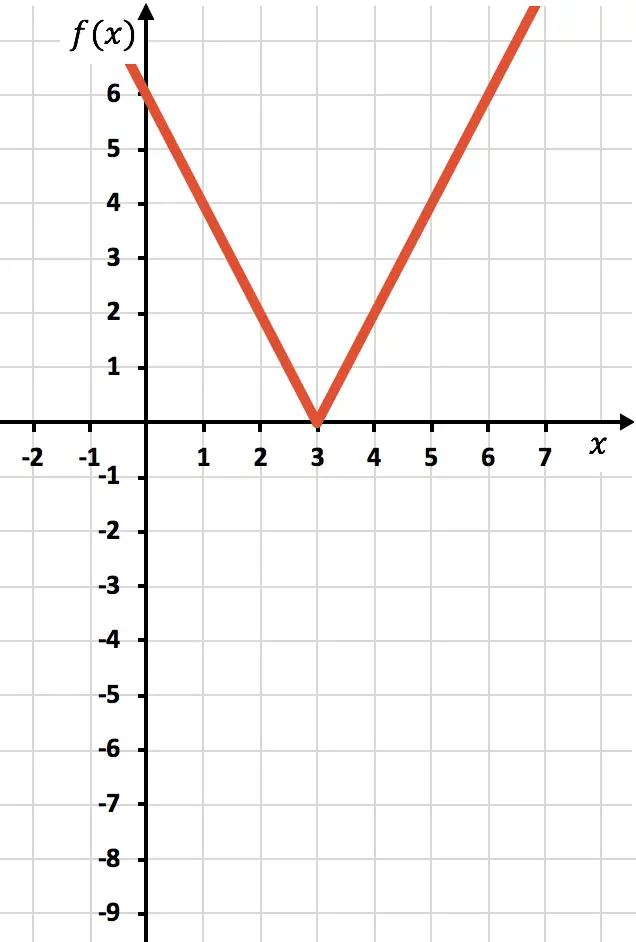
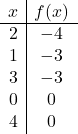
لتمثيل دالة ذات قيمة مطلقة، يجب علينا أولًا تمثيل الدالة بدون القيمة المطلقة. لذلك نجعل جدول قيم الدالة بدون القيمة المطلقة:

$f(x)=-x+2$

$x= 0 \ \longrightarrow \ f(0) = -0+2=2$

$x= 1 \ \longrightarrow \ f(1) = -1+2=1$

$x= 2 \ \longrightarrow \ f(2) = -2+2=0$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 1 \\ 2 & 0 \end{array}$

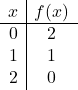
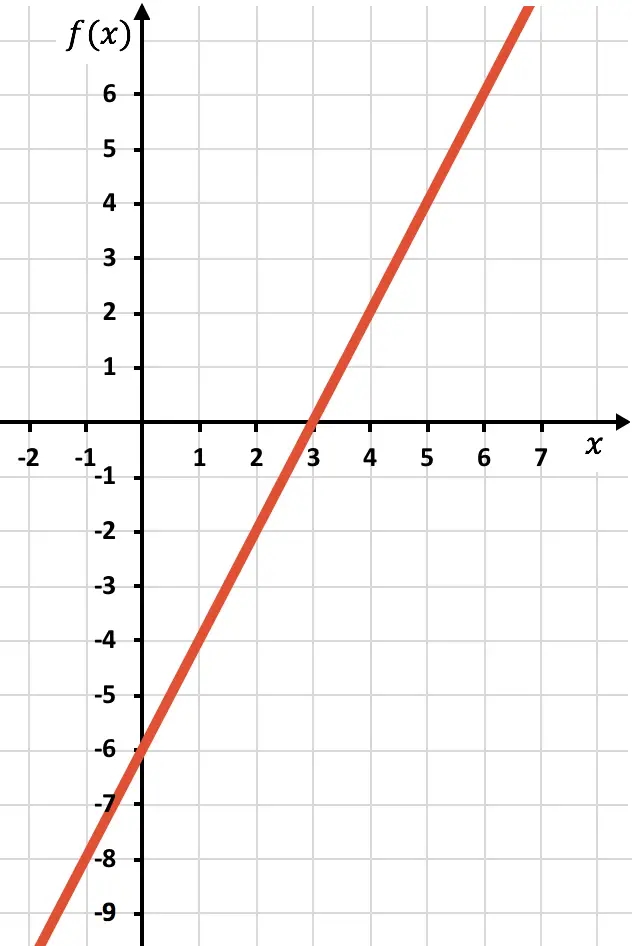
نرسم النقاط رسمًا بيانيًا ونرسم الخط كما لو كانت دالة عادية:

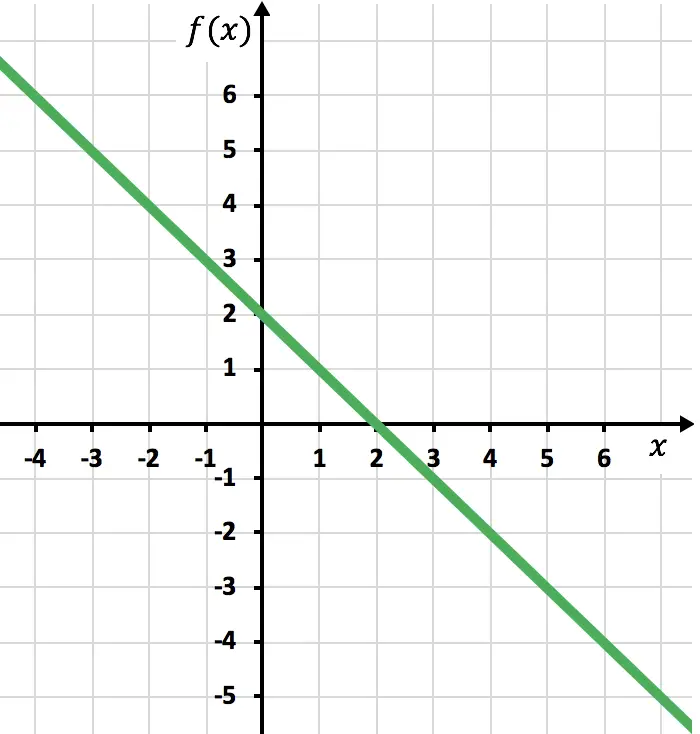
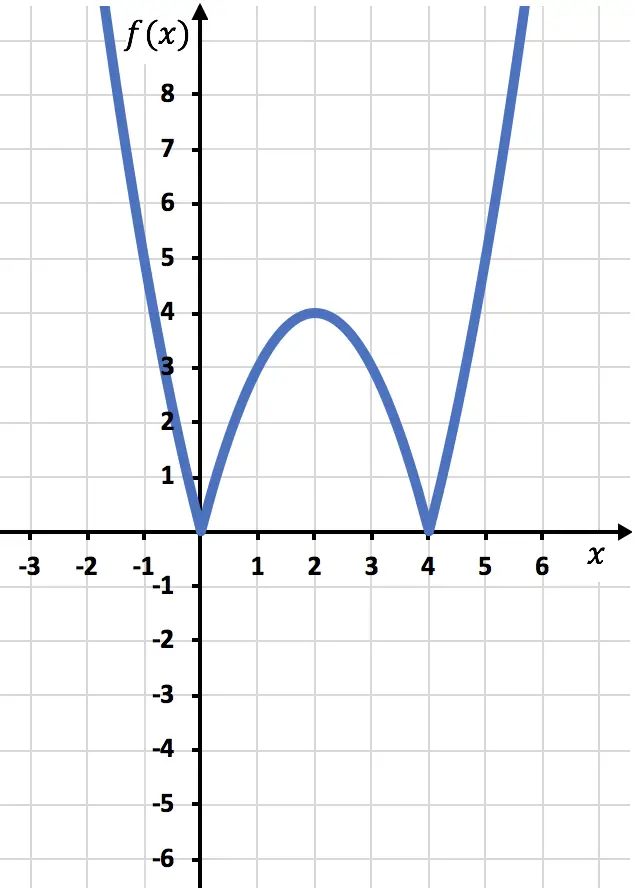
نحتاج الآن إلى رسم الدالة المتماثلة حيث تكون الدالة سالبة، أي حيث تقع أسفل المحور السيني. لذلك، نعكس الدالة بدءًا من x=2:

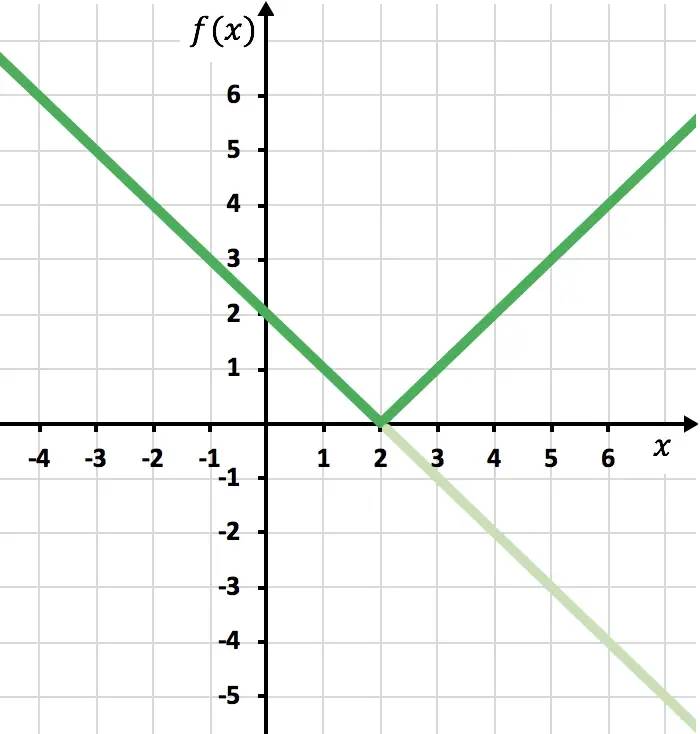
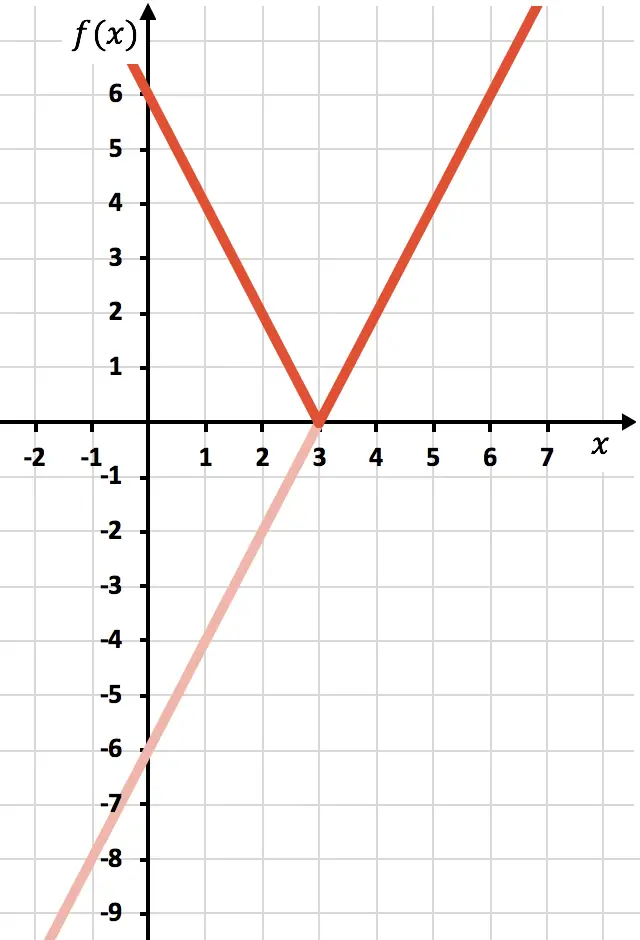
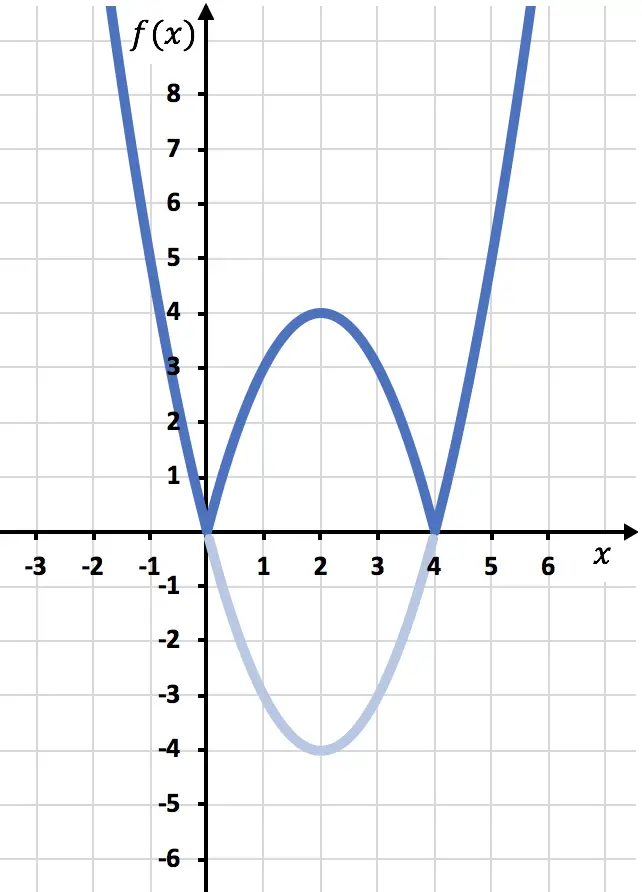
وأخيرًا نحذف أثر الدالة الموجودة أسفل المحور X:

وبهذه الطريقة، نكون قد مثلنا الدالة بقيمة مطلقة. كما رأيت، الشيء الوحيد الذي تغير هو أنه يجب علينا عكس جزء الدالة الموجود أسفل محور OX. ولذلك، فإن الرسم البياني لأي دالة ذات قيمة مطلقة سوف يقع دائمًا على جانب المحور شبه Y الموجب.

من ناحية أخرى، لمراجعة المفاهيم، من الرسم البياني يمكننا أن نستنتج أن مجال دالة القيمة المطلقة السابقة يتكون بالكامل من أرقام حقيقية. من ناحية أخرى، يتكون نطاق أو نطاق الوظيفة المذكورة ذات القيمة المطلقة من أرقام وأصفار موجبة فقط.

تمارين محلولة على دوال القيمة المطلقة

التمرين 1

عبر عن الدالة التالية بقيمة مطلقة في صورة دالة متعددة التعريف:

$f(x)= \lvert -x+3 \rvert$

انظر الحل

أولًا، علينا أن نعرف متى تكون الدالة سالبة. للقيام بذلك، نجعل القيمة المطلقة تساوي الصفر ونحل المعادلة:

$-x+3=0$

$x=3$

نحن نمثل القيمة الموجودة على السطر:

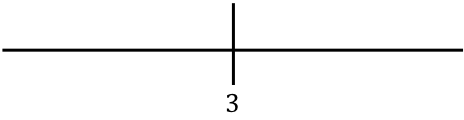
نقوم الآن بتقييم نقطة في كل فترة من الدالة بدون القيمة المطلقة لمعرفة الإشارة التي تحملها الدالة بالفعل في كل قسم من الخط:

$x<3$

على سبيل المثال، نأخذ أي نقطة أقل من 3

$x=0:$

$-0+3$

$+3$

إيجابي

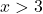$x>3″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”43″ style=”vertical-align: -2px;”> <p class=$ على سبيل المثال، نأخذ أي نقطة أكبر من 3

$x=4:$

$-4+3$

$-1$

سلبي

الدالة بدون القيمة المطلقة ستكون سالبة في الفترة x>3. لذلك يجب علينا التعبير عن الدالة بشرطات عن طريق تغيير علامتها في هذه الفترة:

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] -(-x+3) & \text{si} & x\ge 3 \end{array} \right.$

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] x-3 & \text{si} & x\ge 3 \end{array} \right.$

تمرين 2

أوجد التعبير متعدد التعريف للدالة التالية بقيمة مطلقة:

$f(x)= \lvert 3x^2-75 \rvert$

انظر الحل

أول ما علينا فعله هو تحديد متى تكون الدالة سالبة. للقيام بذلك، علينا أن نجعل وسيطة القيمة المطلقة تساوي الصفر ونحل المعادلة:

$3x^2-75 =0$

$3x^2=75$

$x^2=\cfrac{75}{3}$

$x^2=25$

$x= \pm 5$

نحن الآن نمثل جذور الوظيفة التي تم الحصول عليها على اليمين:

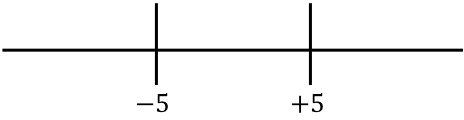
وننظر إلى العلامة التي لها الدالة بدون القيمة المطلقة في كل فترة من الخط:

$x<-5$

على سبيل المثال، نأخذ أي نقطة أقل من -5

$x=-6:$

$3(-6)^2-75$

$108-75$

$+33$

إيجابي

$-5 < x < 5$

نأخذ أي نقطة بين -5 و+5، على سبيل المثال

$x=0:$

$3(0)^2-75$

$0-75$

$-75$

سلبي

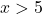$x>5″ title=”Rendered by QuickLaTeX.com” height=”15″ width=”42″ style=”vertical-align: -2px;”> <p class=$ على سبيل المثال، نأخذ أي نقطة أكبر من 5

$x=6:$

$3(6)^2-75$

$108-75$

$+33$

إيجابي

ولذلك، فإن الدالة بدون القيمة المطلقة ستكون سالبة فقط في الفترة -5<x<5. لذلك، نحن بحاجة إلى التعبير عن الدالة في أجزاء عن طريق تغيير إشارة هذه الفترة فقط:

$\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -(3x^2-75) & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”408″ style=”vertical-align: 0px;”> <p style=$

$\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -3x^2+75 & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”394″ style=”vertical-align: 0px;”> <div class=$