ذات الحدين لنيوتن هي صيغة رياضية تستخدم للتعبير عن مجموع حدين مرفوعًا لقوة معينة . هذه الصيغة، التي سميت على اسم عالم الرياضيات البريطاني إسحاق نيوتن، تستخدم في العديد من مجالات الرياضيات.
على سبيل المثال، لها فائدة في الإحصاء، ونظرية الاحتمالات، وحساب التفاضل والتكامل. تسمح لنا نظرية ذات الحدين بحساب قوة ذات الحدين بطريقة بسيطة.
ببساطة، تعتمد ذات الحدين لنيوتن على صيغة يمكن من خلالها حل أي تعبير جبري بالشكل (a+b) n . وعلى الرغم من أن هذه الصيغة تحمل اسم إسحاق نيوتن، إلا أنه من الجدير بالذكر أن هناك جدلاً حول أصلها.
وهذا يعني أن بعض الأبحاث تشير إلى إيجاد استخدام نظرية ذات الحدين في الشرق الأوسط.
متى تم تطوير ذات الحدين لنيوتن؟
تم تطوير نظرية نيوتن ذات الحدين، والمعروفة أيضًا باسم ذات الحدين لنيوتن، في عام 1665 وتم نشرها لأول مرة في رسالتين من مسؤول الجمعية الملكية في عام 1676 .
كانت هذه الرسائل ردًا على عالم الرياضيات الألماني جوتفريد فيلهلم فون لايبنتز، الذي سعى إلى فهم التحقيقات الرياضية في المتسلسلة اللانهائية بشكل أفضل. شارك نيوتن نتائج نظريته وأدرك لايبنتز أنها كانت تقنية مفيدة للحصول على نتائج في التربيعات أو المتسلسلة.
سمحت هذه الملاحظة لنيوتن بأن يستنتج أنه من الممكن العمل على سلسلة لا نهائية بنفس الطريقة كما هو الحال في التعبيرات متعددة الحدود . على الرغم من أن نيوتن لم ينشر نظريته مطلقًا، إلا أن عالم الرياضيات البريطاني جون واليس نشرها في كتابه الجبر عام 1685 ونسب اختراعها إلى نيوتن.
لماذا سميت ذات الحدين لنيوتن؟
سُميت ذات الحدين لنيوتن على اسم عالم الرياضيات والفيزياء الإنجليزي إسحاق نيوتن، الذي طورها في القرن السابع عشر . ولم يكن نيوتن أول من اكتشف هذه النظرية، لكنه كان أول من أثبت صحتها بالنسبة لأي عدد صحيح موجب n.
تعتبر ذات الحدين لنيوتن أداة رياضية مفيدة جدًا في الجبر وحساب التفاضل والتكامل، وتستخدم على نطاق واسع في مجالات مثل الفيزياء والإحصاء والهندسة وعلوم الكمبيوتر.
ما هي صيغة نيوتن ذات الحدين؟
كما ذكرنا سابقًا، فإن ذات الحدين لنيوتن هي الصيغة التي يمكن من خلالها إيجاد قوى ذات الحدين . من أجل العثور على قوة ذات الحدين المذكورة، يتم استخدام “المعاملات ذات الحدين”. يشير المصطلح السابق إلى تسلسل المجموعات.
مع أخذ ذلك في الاعتبار، يمكننا تحليل صيغ نيوتن ذات الحدين على النحو التالي:
- (أ + ب) 2 = أ 2 + 2أ + ب 2
- (أ – ب) 2 = أ 2 – 2أ + ب 2
- (أ + ب) 3 = أ 3 + 3 أ 2 ب + 3 أ 2 + ب 3
تسمى التعبيرات الرياضية التي تشير إلى تطور (a+b) n بالكيانات البارزة، وتتيح الحصول على صيغة عامة تمثل هذه العملية لأي عدد طبيعي “n”.
ومن خلال فحص معاملات كل كثيرة الحدود الناتجة، يمكننا ملاحظة تسلسل يتبع ما يعرف بمثلث باسكال .
يبدأ تسلسل مثلث باسكال بالرقم 1، وفي كل سطر لاحق تكون الأرقام النهائية دائمًا 1. ويتم الحصول على القيم المتوسطة عن طريق إضافة الرقمين من السطر السابق اللذين يقعان مباشرة فوق القيمة المراد حسابها.
كيفية العثور على مصطلح في ذات الحدين نيوتن؟
للعثور على مصطلح محدد في ذات الحدين لنيوتن، يتم استخدام الصيغة العامة:
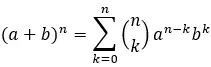
ذهب:
a و b هما معاملات ذات الحدين.
n هو الأس ذو الحدين.
k هو المصطلح المحدد الذي نريد العثور عليه.
Σ يمثل مجموع k=0 إلى n.
[nk] هو المعامل ذو الحدين المحسوب بالصيغة التالية:
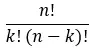
وبالتالي فإن الصيغة الموسعة بالكامل هي كما يلي:
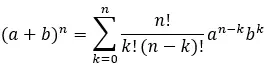
مثال على حل نيوتن ذات الحدين
وبمجرد العثور على هذه القيم، يتم استبدالها في الصيغة ويتم حل التعبير للحصول على المصطلح المحدد. على سبيل المثال، إذا أردنا إيجاد الحد الخامس من ذات الحدين (2x + 3) 6 ، فسيكون لدينا:
واحد = 2x
ب = 3
ن = 6
ك = 5
لذلك، باستخدام الصيغة:
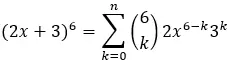
الحد الخامس يتوافق مع k = 5، وبالتالي لدينا:
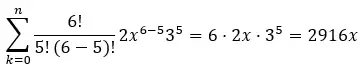
وبالتالي فإن الحد الخامس من ذات الحدين (2x + 3) 6 هو 2916x.
ما هي ذات الحدين نيوتن من الدرجة 5؟
ذات الحدين لنيوتن من الدرجة 5 هي تعبير جبري على الشكل (a + b) 5 ، حيث “a” و “b” متغيران والأس 5 يشير إلى درجة ذات الحدين . بتوسيع هذا التعبير، نحصل على كثيرة الحدود التربيعية التي لها ستة حدود:
(أ + ب) 5 = أ 5 + 5 أ 4 ب + 10 أ 3 ب 2 + 10 أ 2 ب 3 + 5 أ 4 + ب 5
يتم الحصول على كل حد من هذا كثير الحدود من خلال الجمع بين معاملات ذات الحدين مع صلاحيات “أ” و “ب”. على سبيل المثال، يتم الحصول على الحد الثاني (5a 4 b) عن طريق ضرب معامل ذات الحدين (5 اختر 1 = 5) في “a” مرفوعًا إلى الأس الرابع وفي b مرفوعًا إلى الأس الأول.
تعتبر ثنائيات نيوتن من الدرجة الخامسة مفيدة في مختلف فروع الرياضيات والفيزياء، مثل الإحصاء ونظرية الاحتمالات وميكانيكا الكم.
ما هي تطبيقات ذات الحدين نيوتن؟
لدى نيوتن ذات الحدين مجموعة واسعة من التطبيقات في مختلف المجالات، بما في ذلك:
- حساب الاحتمالات : يتم استخدام نظرية ذات الحدين لحساب احتمالات الأحداث ذات الحدين، مثل رمي العملة المعدنية أو نجاح أو فشل سلسلة من الاختبارات.
- نظرية الأعداد – يتم استخدام ذات الحدين لنيوتن لتوسيع كثيرات الحدود وتبسيط المعادلات في نظرية الأعداد.
- الإحصائيات : يتم استخدام ذات الحدين لنيوتن لحساب التوزيعات ذات الحدين وفي بناء فترات الثقة.
- الفيزياء – في الفيزياء، يتم استخدام نظرية ذات الحدين في النظرية النسبية وميكانيكا الكم، من بين مجالات أخرى.
- الاقتصاد والمالية : يتم استخدام ذات الحدين لنيوتن لحساب القيمة الحالية والمستقبلية للتدفقات النقدية مع مرور الوقت وفي تقييم الخيارات المالية.
- البرمجة وعلوم الكمبيوتر : يتم استخدام ذات الحدين لنيوتن في تطوير الخوارزميات وبرمجة الكمبيوتر.
لماذا تعتبر ذات الحدين لنيوتن مهمة؟
تعتبر ذات الحدين لنيوتن ذات صلة لأنها أداة رياضية أساسية لتطوير الجبر ونظرية الأعداد . يسمح لك بحساب نتيجة التربيع أو أي قوة أخرى ذات الحدين، وهو أمر مفيد جدًا لحل المعادلات وتبسيط التعبيرات الجبرية.
بالإضافة إلى ذلك، فإن لها تطبيقات في مجالات مثل الإحصاء والاحتمالات والفيزياء وغيرها. باختصار، تعد ذات الحدين لنيوتن مفهومًا أساسيًا في الرياضيات وفهمها أمر بالغ الأهمية للتقدم في العديد من مجالات الدراسة.
هل هناك طرق أخرى للتعبير عن ذات الحدين لنيوتن؟
نعم، هناك طرق أخرى للتعبير عن ذات الحدين لنيوتن. على سبيل المثال، يمكن التعبير عنها من حيث المعاملات ذات الحدين باستخدام التدوين التوافقي.
بالإضافة إلى ذلك، يمكن التعبير عنها بدلالة الدوال الأسية والدوال المثلثية باستخدام صيغة أويلر. وبالمثل، فيما يتعلق بوظيفة جاما باستخدام صيغة ليجيندر. يمكن أن تكون هذه التعبيرات البديلة مفيدة في سياقات مختلفة ومسائل رياضية.
نيوتن أمثلة ذات الحدين
دعونا بعد ذلك نرى بعض الأمثلة البسيطة لتطبيق ذات الحدين لنيوتن.
مثال 1: احسب حد الرتبة 3 في مفكوك (x + y) 5 .
الحل: في مفكوك (x + y) 5 ، معامل الحد الأول هو 1، معامل الحد الثاني 5، معامل الحد الثالث 10، معامل الحد الرابع 10، ومعامل الحد الخامس هو 5 ومعامل الحد السادس هو 1.
وبالتالي فإن مصطلح الأمر 3 هو:
10× 2 و 3
مثال 2: أوجد الحد المستقل في مفكوك (2x – 1) 4 .
الحل: في مفكوك (2x – 1) 4 ، يوجد الحد المستقل في المجموعة (2x) p (-1) (4-p) حيث p هي القيمة التي تجعل أس (2x) p و (-1) (4-ع) أضف ما يصل إلى 4.
وبالتالي فإن المصطلح المستقل هو:
(2س) 2 (-1) 2 = 4
مثال 3: أوجد الحد الأعلى في مفكوك (3x – 2y) 6 .
الحل: الحد الأعلى في مفكوك (3x – 2y) 6 موجود في المجموعة (3x) p (-2y) (6-p) حيث p هي القيمة التي تجعل الأس ( 3x) p و (-2y) (6-p) تساوي درجة ذات الحدين وهي 6.
ولذلك فإن الحد الأعلى درجة هو:
(3س) 3 (-2ص) 3 = -216س 3 و 3