نقطة متناظرة بالنسبة إلى نقطة أخرى، إلى خط وإلى مستوى

ستجد هنا كيفية حساب نقطة التماثل بالنسبة إلى نقطة أخرى، وفيما يتعلق بالخط، وفيما يتعلق بالمستوى. بالإضافة إلى ذلك، ستتمكن من رؤية الأمثلة والتمارين التي تم حلها خطوة بخطوة.

نقطة متناظرة إلى نقطة أخرى

قبل أن ننظر إلى كيفية حساب النقطة المتناظرة، دعونا نراجع ما هي النقطة المتناظرة بالضبط بالنسبة إلى نقطة أخرى:

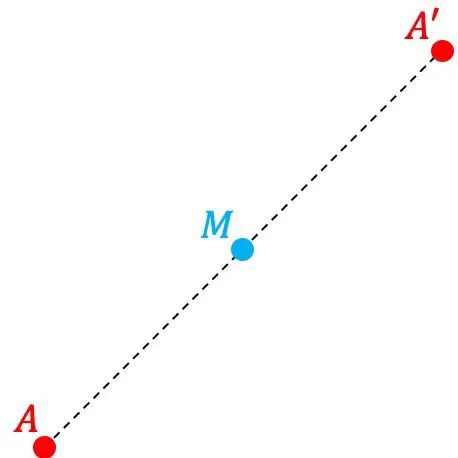
النقطة A’ هي النقطة المتناظرة للنقطة A بالنسبة إلى نقطة أخرى M إذا كانت النقطة A’ تقع بشكل متماثل على نفس المسافة من النقطة M مثل المسافة بين النقطتين A وM. لذلك، M هي نقطة المنتصف للقطعة المكونة من النقطتان أ و أ’.

$d(A,M) = d(A',M )$

ومن ناحية أخرى، نقول أيضًا إن النقطة M هي مركز التماثل.

لذا، لحساب إحداثيات نقطة التماثل، سوف نستخدم صيغة نقطة منتصف القطعة :

$\cfrac{A+A'}{2}=M$

من هذه المعادلة نستخرج النقطة المجهولة A’ ونحصل على صيغة النقطة المتناظرة بالنسبة إلى نقطة أخرى:

$\color{orange} \boxed{ \color{black} \quad A' = 2M - A \quad \vphantom{\Bigl)}}$

مثال على إيجاد نقطة متناظرة بالنسبة إلى نقطة أخرى

على سبيل المثال، سوف نحسب نقطة التماثل للنقطة A بالنسبة للنقطة M. خذ بعين الاعتبار النقطتين:

$A(1,3,0) \qquad \qquad M(-1,4,2)$

ولتحديد نقطة التماثل بين هاتين النقطتين، نطبق صيغة نقطة التماثل بالنسبة إلى نقطة أخرى:

$A' = 2M - A$

الآن نستبدل النقاط في الصيغة:

$A' = 2(-1,4,2) -(1,3,0)$

ونعمل:

$A' = (-2,8,4) -(1,3,0)$

$\bm{A'=(-3,5,4)}$

نقطة متناظرة لخط مستقيم

لقد رأينا للتو فكرة النقطة المتناظرة بالنسبة إلى نقطة أخرى. حسنًا، النقطة المتناظرة لنقطة ما بالنسبة للخط متشابهة جدًا:

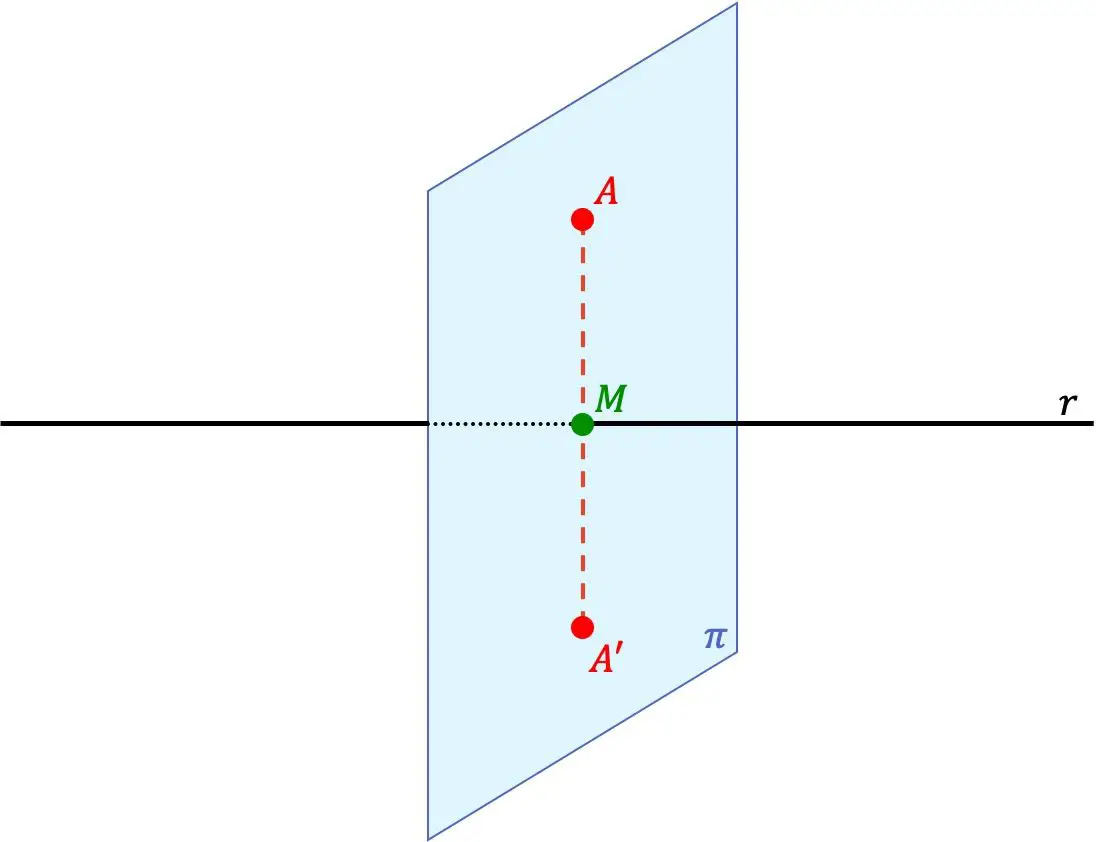
النقطة A’ هي النقطة المتناظرة للنقطة A بالنسبة إلى الخط إذا كانت النقطتان A’ و A’ تقعان على نفس الخط المتعامد على الخط، وعلاوة على ذلك، فإن المسافة بين النقطة A’ والخط تساوي المسافة بين النقطة A والخط.

$d(A,r)= d(A',r)$

لذا فإن الخط r هو أيضًا محور التماثل بين النقاط.

وبالتالي، لتحديد نقطة تناظر النقطة A بالنسبة للمستقيم r ، يجب علينا اتباع الإجراء التالي:

نجد المستوى المتعامد مع الخط r الذي يمر عبر النقطة A (المستوى π من التمثيل البياني السابق). للقيام بذلك، علينا استخدام متجه الاتجاه للخط، والذي سيكون المتجه الطبيعي للمستوى.
نحسب نقطة التقاطع بين المستوى الموجود والخط (النقطة M في الصورة السابقة).
نستخدم صيغة النقطة المتماثلة حول النقطة (الموضحة في القسم أعلاه) للعثور على النقطة المتماثلة للنقطة A بالنسبة للنقطة M. والنتيجة هي النقطة المتماثلة التي كنا نبحث عنها.

مثال لحساب نقطة التماثل بالنسبة للخط

بمجرد أن نعرف كيفية حساب نقطة التماثل لنقطة أخرى بالنسبة لمستقيم، سنرى تمرينًا تم حله كمثال:

أوجد النقطة المتناظرة للنقطة A بالنسبة إلى الخط r. يقال نقطة وسطر:

$\displaystyle A(4,0,-1) \qquad \qquad r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases}$

أولاً، نحتاج إلى حساب المستوى العمودي على الخط r الذي يمر عبر النقطة A. المتجه العمودي لهذا المستوى سيكون متجه الاتجاه للخط، ومكوناته هي الحدود الموجودة أمام المعلمة

$t$

لأنه يتم التعبير عنها في شكل معادلات بارامترية:

$\vv{n}=(1,4,-3)$

والمعاملات A وB وC لمعادلة المستوى تتطابق مع إحداثيات متجهها الطبيعي، وبالتالي:

$\vv{n}=(1,4,-3) \quad \longrightarrow \quad \pi : \ 1x+4y-3z+D=0$

يجب أن تقع النقطة A على هذا المستوى، لذا يمكننا الآن تعويض النقطة A في معادلة المستوى لإيجاد المعامل D:

$A(4,0,-1)$

$4+4\cdot 0-3\cdot (-1)+D=0$

$4+3+D=0$

$7+D=0$

$D=-7$

بحيث تكون معادلة المستوى العمودي على الخط المستقيم الذي يمر بالنقطة A هي:

$\pi : \ x+4y-3z-7=0$

بمجرد أن نعرف معادلة المستوى، علينا حساب نقطة تقاطع المستوى مع الخط. للقيام بذلك، نعوض بإحداثيات الخط في معادلة المستوى ونحل المعادلة الناتجة:

$\displaystyle r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases} \qquad \qquad \pi : \ x+4y-3z-7=0$

$(1+t)+4(5+4t)-3(-4-3t)-7=0$

$1+t+20+16t+12+9t-7=0$

$26t+26=0$

$26t=-26$

$t=\cfrac{-26}{26}$

$t=-1$

الآن نستبدل قيمة

$t$

تم الحصول عليها في معادلة الخط:

$\displaystyle t=-1 \ \longrightarrow \ \begin{cases}x=1 -1=0 \\[1.7ex] y=5 +4\cdot (-1)=1\\[1.7ex] z=-4-3\cdot (-1)=-1 \end{cases}$

إذن نقطة التقاطع بين المستقيم r والمستوى العمودي عليه هي:

$M(0,1,-1)$

وأخيرًا، يكفي إيجاد النقطة المتماثلة للنقطة A بالنسبة للنقطة M؛ ولهذا يمكننا استخدام الصيغة الموضحة في بداية هذه الصفحة:

$\begin{aligned} A' & = 2M - A \\[2ex] &= 2(0,1,-1) - (4,0,-1) \\[2ex] & = (0,2,-2)-(4,0,-1)\\[2ex] & = \bm{(-4,2,-1)} \end{aligned}$

نقطة متناظرة إلى الطائرة

قبل الاطلاع على طريقة تحديد نقطة تماثل نقطة أخرى بالنسبة إلى المستوى، دعونا نرى ما هو تعريفها:

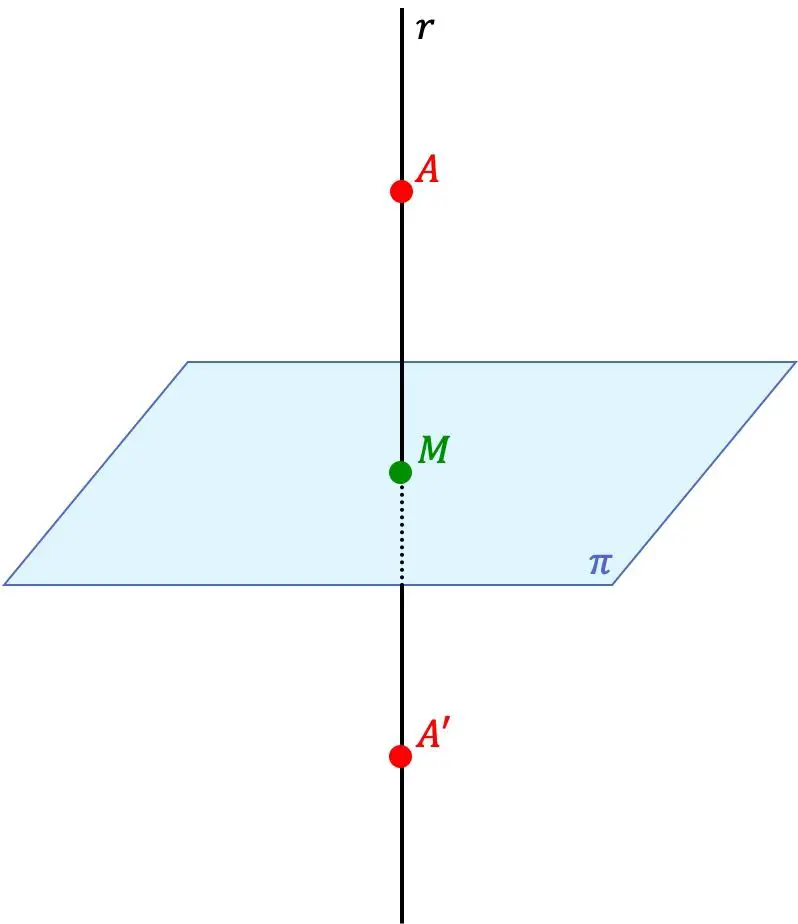
النقطة A’ هي النقطة المتناظرة للنقطة A بالنسبة إلى المستوى إذا كانت النقطتان A’ و A تقعان على نفس الخط المتعامد على المستوى، وعلاوة على ذلك، فإن المسافة بين النقطة A’ والمستوى تعادل المسافة بين النقطة A والمستوى.

نقطة متناظرة إلى نقطة أخرى بالنسبة للطائرة

$d(A,\pi)= d(A',\pi)$

إذن، المستوى هو أيضًا مستوى تماثل بين النقطتين.

وبالتالي، لمعرفة الإحداثيات الديكارتية للنقطة المتناظرة للنقطة A بالنسبة للمستوى π، عليك اتباع الخطوات التالية:

نجد معادلة الخط العمودي على المستوى الذي يمر بالنقطة A. ولهذا سنستخدم المتجه العمودي على المستوى باعتباره متجه الاتجاه للخط.
نحسب نقطة التقاطع بين المستوى والخط الموجود (النقطة M في الصورة السابقة).
نستخدم صيغة النقطة المتماثلة حول النقطة (الموضحة في قسم البداية) للعثور على النقطة المتماثلة للنقطة A بالنسبة للنقطة M. والنتيجة هي النقطة المتماثلة التي كنا نبحث عنها.

مثال على تحديد نقطة التماثل بالنسبة للمستوى

يمكنك أدناه رؤية مشكلة تم حلها فيما يتعلق بنقطة تناظر نقطة أخرى بالنسبة إلى المستوى:

تحديد نقطة التماثل لـ A بالنسبة للمستوى π. وبعد أن قلت النقطة والخطة:

$\displaystyle A(3,-4,2) \qquad \qquad \pi: \ 2x+y-z-6=0$

أول ما يتعين علينا القيام به هو إيجاد معادلة الخط العمودي على المستوى والذي يمر بالنقطة A. للقيام بذلك، يمكننا استخدام المتجه العمودي على المستوى باعتباره متجه الاتجاه للخط الذي مكوناته X، Y وZ هي معاملات الحدود A وB وC على التوالي لمعادلة المستوى:

$\pi: \ 2x+y-z-6=0 \quad \longrightarrow \quad \vv{n} = (2,1,-1)$