نقاط انعطاف الدالة -

نوضح هنا ما هي نقطة انعطاف الدالة وكيفية العثور على جميع نقاط انعطاف الدالة. بالإضافة إلى ذلك، ستجد تمارين خطوة بخطوة حول انحناء الدالة ونقاط انعطافها.

ما هي نقاط انعطاف وظيفة؟

نقاط انعطاف الدالة هي النقاط التي يتغير عندها الرسم البياني للدالة انحناء، أي عند نقطة انعطاف تتغير الدالة من مقعرة إلى محدبة أو العكس.

كيفية معرفة ما إذا كانت الوظيفة لها نقطة انعطاف

نظرا لتعريف نقطة انعطاف، دعونا نرى كيفية معرفة ما إذا كانت نقطة معينة هي نقطة انعطاف للوظيفة.

الدالة لها نقطة انعطاف عند نقاط تلغي مشتقتها الثانية ومشتقتها الثالثة ليست صفرًا.

$\left.\begin{array}{l}f''(a)=0\\[2ex]f'''(a)\neq 0\end{array}\right\} \quad \bm{\longrightarrow} \quad x=a \text{ es un punto de inflexi\'on}$

على سبيل المثال، سوف نقوم بحساب نقاط انعطاف دالة الدرجة الثالثة التالية:

$f(x)=x^3-5x$

أولاً نحسب المشتقتين الثانية والثالثة للدالة:

$f'(x)=3x^2-5$

$f''(x)=6x$

$f'''(x)=6$

الآن نجعل المشتقة الثانية تساوي 0 ونحل المعادلة الناتجة:

$6x=0$

$x=0$

إذن، النقطة x=0 ستكون نقطة انقلاب للدالة إذا كانت المشتقة الثالثة غير صفرية عند هذه النقطة. في حالتنا، المشتقة الثالثة تساوي دائمًا 6.

$f'''(0)=6\neq 0$

لذلك، x=0 هي نقطة انعطاف للدالة.

كيفية دراسة الانحناء وإيجاد نقاط انعطاف الدالة

لقد رأينا للتو طريقة للعثور على نقاط التحول. ومع ذلك، فإننا نميل عادةً إلى دراسة انحناء الدالة، أي تحديد تقعر وتحدب الدالة، ومن هناك نحسب نقاط الانقلاب.

للعثور على نقاط انعطاف دالة من خلال انحناءها، يجب تنفيذ الخطوات التالية:

أوجد النقاط التي لا تنتمي إلى مجال الدالة .
احسب المشتقة الأولى والمشتقة الثانية للدالة.
أوجد جذور المشتقة الثانية ، أي احسب النقاط التي تلغي المشتقة الثانية بالحل
$f''(x)=0$

.
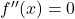
قم بعمل فترات زمنية مع جذور المشتقة والنقاط التي لا تنتمي إلى مجال الدالة.
احسب قيمة المشتقة الثانية عند نقطة في كل فترة.
تحدد إشارة المشتق الثاني تقعر أو تحدب الدالة في هذه الفترة:
- إذا كانت المشتقة الثانية للدالة موجبة، تكون الدالة محدبة في هذه الفترة.
- إذا كانت المشتقة الثانية للدالة سالبة، تكون الدالة مقعرة في هذه الفترة.
نقاط الانعطاف هي النقاط التي تتغير عندها الدالة من محدبة إلى مقعرة أو العكس.

لكي تتمكن من رؤية كيفية حساب نقاط انعطاف الدالة باستخدام هذا الإجراء، سنحل مثالًا خطوة بخطوة أدناه:

ادرس الانحناء وأوجد نقاط انعطاف الدالة متعددة الحدود التالية:

$f(x)=x^4-6x^2$

أول شيء يجب فعله هو حساب مجال تعريف الدالة. إنها دالة متعددة الحدود، لذا فإن مجال الدالة يتكون من أعداد حقيقية، أي أنها دالة متصلة:

$\text{Dom } f= \mathbb{R}$

بمجرد أن نحسب مجال الدالة، نحتاج إلى دراسة النقاط التي تتحقق عندها

$f''(x)=0$

لذلك نحسب أولاً المشتقة الأولى للدالة:

$f(x)=x^4-6x^2 \ \longrightarrow \ f'(x)= 4x^3-12x$

بعد ذلك، نحسب المشتقة الثانية للدالة:

$f'(x)=4x^3-12x \ \longrightarrow \ f''(x)= 12x^2-12$

والآن نجعل المشتقة الثانية تساوي 0 ونحل المعادلة:

$f''(x)=0$

$12x^2-12=0$

$12x^2=12$

$x^2=\cfrac{12}{12}$

$x^2=1$

$\sqrt{x^2}=\sqrt{1}$

$x=\pm1$

بمجرد أن نحسب مجال الوظيفة و

$f''(x)=0$

، نحن نمثل جميع النقاط الحرجة الموجودة على خط الأعداد:

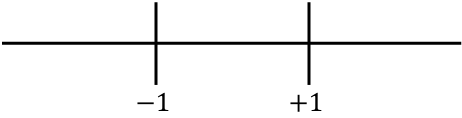
والآن نحسب إشارة المشتقة الثانية في كل فترة لنعرف ما إذا كانت الدالة مقعرة أم محدبة. لذلك نأخذ نقطة في كل فترة (وليس النقاط الحرجة أبدًا) وننظر إلى الإشارة التي يحملها المشتق الثاني عند هذه النقطة:

$f''(x)=12x^2-12$

$f''(-2) = 12\cdot (-2)^2-12 =36 \ \rightarrow \ \bm{+}$

$f''(0) = 12\cdot 0^2-12 = -12 \ \rightarrow \ \bm{-}$

$f''(2) = 12\cdot 2^2-12=36 \ \rightarrow \ \bm{+}$

إذا كانت المشتقة الثانية موجبة، فهذا يعني أن الدالة محدبة.

$(\bm{\cup})$

وإذا كانت المشتقة الثانية سالبة فهذا يعني أن الدالة مقعرة

$(\bm{\cap})$

. وبالتالي فإن فترات التقعر والتحدب للدالة هي:

محدب

$(\bm{\cup})$

$\bm{(-\infty,-1) \cup (1,+\infty)}$

مقعر

$(\bm{\cap})$

$\bm{(-1,1)}$

علاوة على ذلك، عند x=-1، تنتقل الدالة من محدبة إلى مقعرة، لذا فإن x=-1 هي نقطة انقلاب للدالة . وعند x=1، تنتقل الدالة من مقعرة إلى محدبة، لذا فإن x=1 هي أيضًا نقطة انقلاب للدالة.

أخيرًا، نعوض بالنقاط الموجودة في الدالة الأصلية لإيجاد الإحداثي Y لنقاط الانقلاب:

$f(-1)=(-1)^4-6(-1)^2 = 1-6 \cdot 1 = -5 \ \longrightarrow \ (-1,-5)$

$f(1)=1^4-6\cdot 1^2 = 1-6 \cdot 1 = -5 \ \longrightarrow \ (1,-5)$

وبالتالي فإن نقاط التحول في الوظيفة هي:

نقطة تحول:

$\bm{(-1,-5)}$

$\bm{(1,-5)}$

يمكنك أدناه رؤية التمثيل البياني للوظيفة التي تمت دراستها:

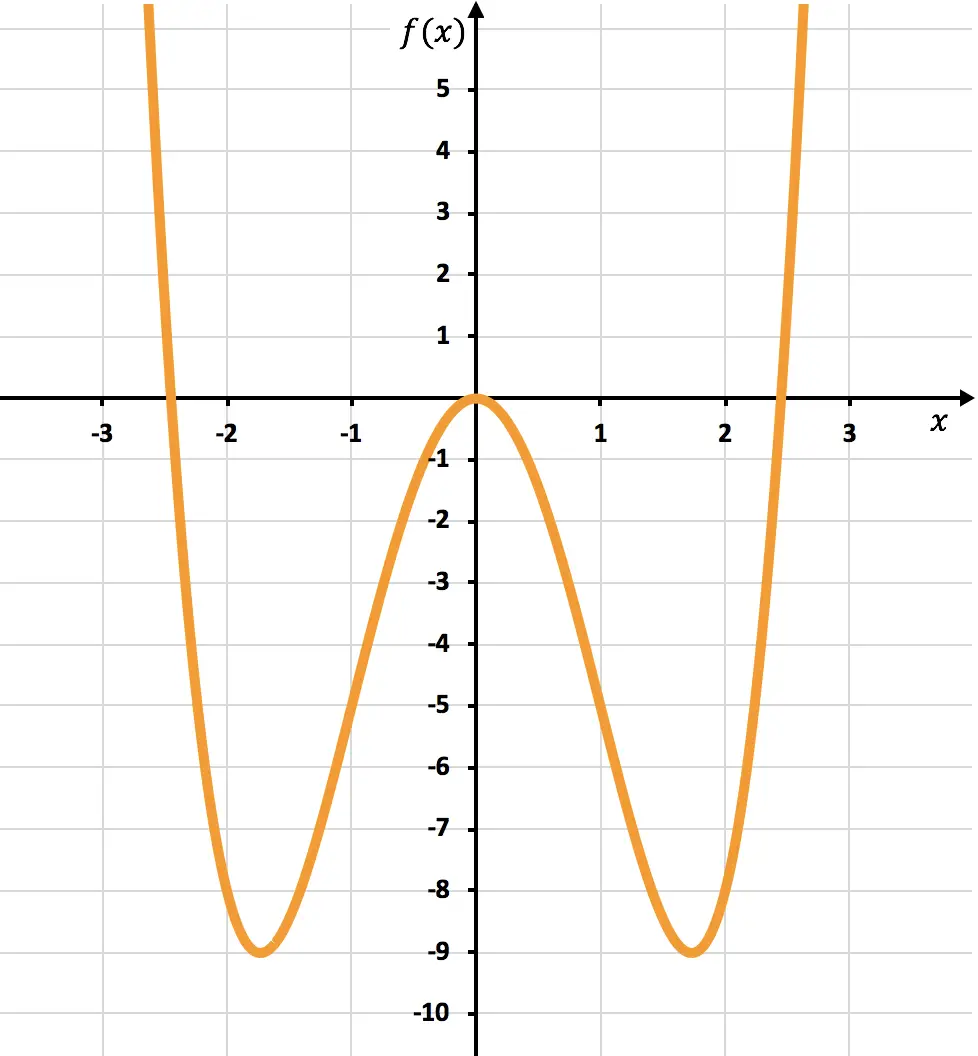
كما ترون من الرسم البياني، فإن الدالة تنتقل من محدبة

$(\cup)$

أن تكون مقعرة

$(\cap)$

عن

$(-1,-5)$

منذ أن تغير انحناءها. ومن ناحية أخرى، تنتقل الدالة من التقعر

$(\cap)$

تكون محدبة

$(\cup)$

عن

$(1,-5)$

حل تمارين الدوران

التمرين 1

احسب فترات التقعر والتحدب بالإضافة إلى نقاط انعطاف الدالة الأسية التالية:

$f(x) = xe^x$

انظر الحل

أول شيء يجب فعله هو حساب مجال تعريف الدالة. تتكون الدالة من دالة متعددة الحدود (x)، يتكون مجالها من أرقام حقيقية فقط، ودالة أسية (e ^x ) ، يتكون مجالها أيضًا من أرقام حقيقية. وبالتالي فإن مجال الدالة يتكون من أعداد حقيقية:

$\text{Dom } f= \mathbb{R}$

الآن دعونا نحسب مشتقة الدالة. في هذه الحالة، تتكون الدالة من حاصل ضرب دالتين، لذلك لاشتقاق الدالة نحتاج إلى تطبيق صيغة مشتقة حاصل الضرب:

$f'(x)=1 \cdot e^x+ x \cdot e^x$

$f'(x)=e^x +xe^x$

بعد ذلك، نحسب المشتقة الثانية للدالة:

$f''(x)= e^x + 1 \cdot e^x+ x \cdot e^x$

$f''(x)=e^x +e^x + xe^x = 2e^x +xe^x$

نجعل المشتقة الثانية تساوي 0 ونحل المعادلة:

$f''(x)= 0$

$2e^x+xe^x= 0$

نستخرج العامل المشترك :

$e^x(2+x)=0$

لكي يكون الضرب يساوي 0، يجب أن يكون أحد عنصري الضرب صفراً. ولذلك، فإننا نجعل كل عامل يساوي 0:

$\displaystyle e^x\cdot(2+x) =0 \longrightarrow \begin{cases} e^x=0 \ \color{red}\bm{\times}\color{black} \\[2ex] 2+x=0 \ \longrightarrow \ x= - 2 \end{cases}$

الرقم المرفوع إلى رقم آخر لا يمكن أن ينتج عنه 0. لذلك، المعادلة

$e^x=0$

لا يوجد حل.

نحن نمثل جميع النقاط الفردية التي تم الحصول عليها على اليمين:

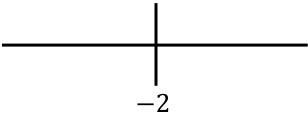
والآن نحسب إشارة المشتقة الثانية في كل فترة لنعرف هل الدالة مقعرة أم محدبة. للقيام بذلك، نأخذ نقطة في كل فترة وننظر إلى العلامة التي لها المشتقة الثانية عند تلك النقطة:

$f''(-3)= 2e^{-3} +(-3)\cdot e^{-3} = 0,1 - 0,15 = -0,05\ \rightarrow \ \bm{-}$

$f''(0)= 2e^0 +0\cdot e^0 = 2 \cdot 1 + 0 \cdot 1 =2+0= 2 \ \rightarrow \ \bm{+}$

إذا كانت المشتقة الثانية موجبة، فهذا يعني أن الدالة محدبة.

$(\bm{\cup})$

وإذا كانت المشتقة الثانية سالبة فهذا يعني أن الدالة مقعرة

$(\bm{\cap})$

. وبالتالي فإن فترات التقعر والتحدب هي:

محدب

$(\bm{\cup})$

$\bm{(-2,+\infty)}$

مقعر

$(\bm{\cap})$

$\bm{(-\infty,-2)}$

بالإضافة إلى ذلك، تتغير الدالة من مقعرة إلى محدبة عند x=-2، لذا فإن x=-2 هي نقطة انقلاب للدالة.

أخيرًا، نعوض بنقطة الانعطاف الموجودة في الدالة الأصلية لإيجاد الإحداثي Y للنقطة:

$f(-2) = (-2)\cdot e^{-2} =-2e^{-2} \ \longrightarrow \ (-2,-2e^{-2})$

في الختام، نقاط التحول الوحيدة للوظيفة هي:

نقطة تحول:

$\bm{(-2,-2e^{-2})}$

تمرين 2

ادرس فترات التقعر والتحدب وأوجد نقاط انعطاف الدالة الكسرية التالية:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

انظر الحل

نحتاج أولاً إلى حساب مجال الوظيفة. وبما أن هذه دالة كسرية، فقد جعلنا المقام يساوي الصفر لمعرفة الأرقام التي لا تنتمي إلى مجال الدالة:

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

هذا يعني أنه عندما تكون x -2 أو +2، فإن المقام سيكون 0. وبالتالي، لن تكون الدالة موجودة. وبالتالي فإن مجال الدالة يتكون من جميع الأرقام باستثناء x=-2 وx=+2.

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

ثانياً، نحسب المشتقة الأولى للدالة:

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

ثم نحل المشتقة الثانية:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

يتم ضرب جميع المصطلحات بـ

$(x^2-4)$

. يمكننا بالتالي تبسيط الكسر:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

الآن دعونا نحسب جذور المشتق الثاني للدالة:

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

على المدى

$\left(x^2-4\right)^3$

يتضمن ذلك تقسيم الجانب الأيسر بأكمله، حتى نتمكن من ضربه في الجانب الأيمن بأكمله:

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

نستخرج العامل المشترك :

$x(8x^2+96)=0$

لكي يكون الضرب يساوي 0، يجب أن يكون أحد عنصري الضرب صفراً. ولذلك، فإننا نجعل كل عامل يساوي 0:

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$

لا يوجد حل لأنه لا يوجد جذر سلبي لعدد حقيقي.

نمثل الآن على الخط جميع النقاط الحرجة التي تم الحصول عليها، أي النقاط التي لا تنتمي إلى المجال (x=-2 وx=+2) وتلك التي تلغي المشتقة الثانية (x=0):

ونحسب إشارة المشتقة الثانية في كل فترة لنعرف ما إذا كانت الدالة مقعرة أم محدبة. لذلك نأخذ نقطة في كل فترة وننظر إلى الإشارة التي تحتوي على المشتقة الثانية عند تلك النقطة:

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

إذا كانت المشتقة الثانية موجبة، فهذا يعني أن الدالة محدبة.

$(\bm{\cup})$

وإذا كانت المشتقة الثانية سالبة فهذا يعني أن الدالة مقعرة

$(\bm{\cap})$

. وبالتالي فإن فترات التقعر والتحدب هي:

محدب

$(\bm{\cup})$

$\bm{(-2,0)\cup (2,+\infty)}$

مقعر

$(\bm{\cap})$

$\bm{(-\infty,-2)\cup (0,2)}$

تغير الدالة الانحناء عند ثلاث نقاط، وبالتالي فإن الدالة المنطقية من حيث المبدأ سيكون لها ثلاث نقاط انقلاب، وهي x=-2، x=0 وx=2. ومع ذلك، على الرغم من وجود تغيير في الانحناء عند x=-2 وعند x=+2، إلا أن هذه ليست نقاط انعطاف لأنها لا تنتمي إلى مجال الدالة. من ناحية أخرى، عند x=0 هناك تغيير في الانحناء وهذا ينتمي إلى الدالة، لذا فإن x=0 هي نقطة الانعطاف الوحيدة للدالة.

كل ما تبقى هو حساب الإحداثي Y لنقطة الانقلاب:

$\displaystyle f(0)=\frac{0^3}{0^2-4} =\frac{0}{-4}=0\ \longrightarrow \ (0,0)$