نظرية فايرستراس

ستجد في هذه المقالة تعريف نظرية Weierstrass. بالإضافة إلى ذلك، سوف تكون قادرًا على التدرب على العديد من التمارين التي تم حلها خطوة بخطوة لنظرية Weierstrass لفهمها بشكل مثالي.

بيان نظرية فايرستراس

تنص نظرية فايرستراس على أنه إذا كانت الدالة متصلة على فترة مغلقة، فإن تلك الدالة لها قيمة عظمى مطلقة وقيمة صغرى مطلقة في تلك الفترة.

➤ انظر: ما هي الوظيفة المستمرة؟

تنص نظرية فايرستراس فقط على وجود حد أقصى وأدنى، ولكن ليس من المفيد حساب قيم هذه النقاط.

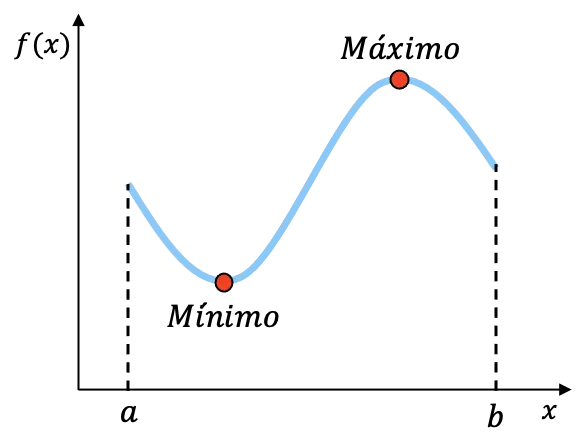
على سبيل المثال، الدالة الموضحة أعلاه متصلة على الفترة [a,b] ولها قيمة صغرى وقيمة عظمى في هذه الفترة. على الرغم من أننا لا نستطيع معرفة الإحداثيات الدقيقة لهاتين النقطتين، فإننا نعلم أن الدالة لها نقطتي النهاية هاتين في الفترة.

➤ انظر: كيفية حساب الحد الأقصى والحد الأدنى للدالة

بما أن الدالة متصلة خلال الفترة بأكملها، فهذا يعني أنها ستأخذ أيضًا جميع القيم الممكنة بين الحد الأدنى المطلق والحد الأقصى المطلق خلال نفس الفترة.

علاوة على ذلك، كنتيجة لنظرية فايرستراس، يمكن للمرء أن يستنتج أن أي دالة متصلة في فترة مغلقة تكون محدودة من الأعلى والأسفل ، والحدين العلوي والسفلي للدالة هما الحد الأقصى والحد الأدنى المطلقان، على التوالي.

رياضياً، يمكن التعبير عن نظرية فايرستراس على النحو التالي:

$f(x_1)\leq f(x)\leq f(x_2)$

ذهب

$x_1$

$x_2$

نقطتان متضمنتان (الحد الأدنى المطلق والحد الأقصى المطلق على التوالي) في الفترة المغلقة

$[a,b]$

حيث يتم تعريف الوظيفة.

إن إثبات نظرية فايرستراس معقد للغاية ولا يساهم كثيرًا في المفهوم، لذلك لن نشرحه في هذه المقالة. الشيء المهم هو أن تفهم ما هي نظرية Weierstrass وفيم تُستخدم.

نظرية Weierstrass حلت المشاكل

التمرين 1

حدد ما إذا كانت الدالة التالية محدودة بالفاصل الزمني المقترح:

$f(x)=\log_3(x-4) \qquad x \in [5,10]$

➤ انظر: مجال الدالة اللوغاريتمية

انظر الحل

يمكننا تحديد ما إذا كانت الدالة محدودة بالفاصل الزمني [5،10] من خلال تطبيق نظرية فايرستراس. لذلك يجب علينا معرفة ما إذا كانت الدالة متصلة في هذه الفترة، وللقيام بذلك نحسب مجال الدالة اللوغاريتمية:

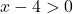
$x-4>0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”73″ style=”vertical-align: -2px;”></p> </p> <p style=$

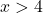
$x>4″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”43″ style=”vertical-align: -2px;”></p> </p> <p style=$

$\text{Dom } f = (4,+\infty)$

الدالة مستمرة لجميع القيم الأكبر من x=4، لذا فهي مستمرة على الفترة [5،10].

ولذلك، فإن الدالة تحقق نظرية فايرستراس على الفترة [5،10]، مما يعني أنها محصورة من الأعلى والأسفل في هذه الفترة.

تمرين 2

حدد ما إذا كانت الدالة التالية لها الحد الأقصى و/أو الحد الأدنى خلال الفترة الزمنية المقترحة:

$f(x)=\cfrac{3x^2-4}{2x-4} \qquad x \in [-3,3]$

➤ انظر: مجال الدالة العقلانية

انظر الحل

أولا، نقوم بتحليل استمرارية الوظيفة العقلانية:

$2x-4=0$

$2x=4$

$x=\cfrac{4}{2}=2$

$\text{Dom } f = \mathbb{R}- \{ 2\}$

ومع ذلك، فإن الدالة تظهر انقطاعًا عند x=2، مما يعني أنها غير متصلة على الفترة [-3,3].

باختصار، الدالة لا تلبي نظرية فايرستراس وبالتالي لا يمكننا القول ما إذا كان لها حد أدنى أو أقصى في هذه الفترة.

التمرين 3

حدد ما إذا كانت الدالة التالية لها حد أقصى و/أو أدنى في الفاصل الزمني المقترح واحسب هذه النقاط:

$f(x)=x^2+3 \qquad x \in [0,4]$

➤ انظر: خصائص الدوال التربيعية

انظر الحل

مجال أي دالة تربيعية هو جميع الأعداد الحقيقية:

$\text{Dom } f=\mathbb{R}$

وبالتالي فإن الدالة مستمرة على الفترة [0,4] وتحقق نظرية فايرستراس. ومن ثم، فإن الدالة لها قيمة صغرى مطلقة وقيمة عظمى مطلقة في هذه الفترة.

علاوة على ذلك، فإن قمة هذا القطع المكافئ تكون بالضبط عند x=0، وبالتالي فإن الدالة تتزايد بشكل صارم على الفترة [0,4] وبالتالي، الحد الأدنى عند x=0 والحد الأقصى عند x= 4 .

$\text{M\'inimo en } x=0 \ \longrightarrow \ f(0)=0^2+3=3$

$\text{M\'aximo en } x=4 \ \longrightarrow \ f(4)=4^2+3=19$

كارل فايرستراس

وبمجرد أن رأينا ما تعنيه نظرية فايرستراس، سنشرح بإيجاز من هو مخزون هذه النظرية.

كان كارل تيودور فيلهلم فايرستراس عالم رياضيات ألماني مهم للغاية في القرن التاسع عشر، وبشكل أكثر دقة، ولد في 31 أكتوبر 1815 في أوستنفيلد وتوفي في 19 فبراير 1897 في برلين.

بالإضافة إلى نظرية فايرستراس، فهو معروف أيضًا بمساهماته الأخرى في الرياضيات. ومن بينها، أعطى تعريفات الاستمرارية والحد والمشتقة، وهي ثلاثة مفاهيم مهمة جدًا للوظائف.

كما تمكن من إثبات بعض النظريات التي لم يتم التحقق منها رياضيًا في ذلك الوقت، مثل نظرية بولزانو-فايرستراس، أو نظرية القيمة المتوسطة، أو نظرية هاين-بوريل.

من باب الفضول، هناك حفرة قمرية وكويكب سمي على اسم فايرستراس تكريما له.

نظرية ويرستراس

بيان نظرية فايرستراس

نظرية Weierstrass حلت المشاكل

التمرين 1

تمرين 2

التمرين 3

كارل فايرستراس

اترك تعليقاً إلغاء الرد