نظرية روش – فريبينيوس

في هذه الصفحة سوف نكتشف ما هي نظرية روشيه فروبينيوس وكيفية حساب رتبة المصفوفة بها. ستجد أيضًا أمثلة وتمارين تم حلها خطوة بخطوة باستخدام نظرية روشيه-فروبينيوس.

ما هي نظرية روشيه-فروبينيوس؟

نظرية روشيه فروبينيوس هي طريقة لتصنيف أنظمة المعادلات الخطية. بمعنى آخر، يتم استخدام نظرية روشيه-فروبينيوس لمعرفة عدد الحلول الموجودة في نظام المعادلات دون الحاجة إلى حلها.

هناك 3 أنواع من أنظمة المعادلات:

تحديد توافق النظام (SCD): يتمتع النظام بحل فريد.
نظام متوافق غير محدد (ICS): النظام لديه حلول لا حصر لها.
النظام غير متوافق (SI): لا يوجد حل للنظام.

بالإضافة إلى ذلك، ستسمح لنا نظرية روشيه-فروبينيوس لاحقًا بحل الأنظمة باستخدام قاعدة كرامر .

بيان نظرية روشيه-فروبينيوس

تقول نظرية روشيه-فروبينيوس ذلك

$\displaystyle \bm{A}$

هي المصفوفة التي تتكون من معاملات المجهولة لنظام المعادلات. والبطن

$\displaystyle \bm{A'}$

أو المصفوفة الموسعة هي المصفوفة المكونة من معاملات المجهول لنظام المعادلات والمصطلحات المستقلة:

تتيح لنا نظرية روشيه-فروبينيوس معرفة نوع نظام المعادلات الذي نتعامل معه وفقًا لرتبة المصفوفتين A و A’:

إذا كانت الرتبة (A) = الرتبة (A’) = عدد المجهولين ⟶ تحديد النظام المتوافق (SCD)
إذا كانت الرتبة (A) = الرتبة (A’) < عدد العناصر المجهولة ⟶ نظام متوافق غير محدد (SCI)
إذا كان النطاق (أ)
$\bm{\neq}$

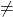
النطاق (A’) ⟶ نظام غير متوافق (SI)

بمجرد أن نعرف ما تقوله نظرية روشيه-فروبينيوس، سنرى كيفية حل تمارين نظرية روشيه-فروبينيوس. فيما يلي 3 أمثلة: تمرين تم حله باستخدام نظرية كل نوع من أنظمة المعادلات.

مثال على النظام المتوافق المحدد (SCD)

$\begin{cases} 2x+y-3z=0 \\[1.5ex] x+2y-z= 1 \\[1.5ex] 4x-2y+z = 3\end{cases}$

المصفوفة A والمصفوفة الموسعة A’ للنظام هما:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 1 & 2 & -1 & 1 \\[1.1ex] 4 & -2 & 1 & 3\end{array} \right)$

نحسب الآن رتبة المصفوفة A. للقيام بذلك، نتحقق مما إذا كان محدد المصفوفة بأكملها مختلفًا عن 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{vmatrix} = 25 \neq 0$

بما أن المصفوفة لها محدد 3×3 يختلف عن 0، فإن المصفوفة A لها المرتبة 3:

$\displaystyle rg(A)=3$

بمجرد أن نعرف رتبة A، نحسب رتبة A’، والتي ستكون على الأقل المرتبة 3 لأننا رأينا للتو أنها تحتوي على محدد من الرتبة 3 يختلف عن 0. علاوة على ذلك، لا يمكن أن تكون من الرتبة 4، نظرًا لأنه لا يمكننا إنشاء أي محدد للرتبة 4. لذلك، فإن المصفوفة A’ هي أيضًا من المرتبة 3:

$\displaystyle rg(A')=3$

وبالتالي، بما أن رتبة المصفوفة A تساوي رتبة المصفوفة A’ وعدد مجاهيل النظام (3)، فإننا نعرف من خلال نظرية روش فروبينيوس أنه نظام محدد متوافق (SCD). :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

مثال على نظام متوافق غير محدد (ICS)

$\begin{cases} x-y+2z=1 \\[1.5ex] 3x+2y+z= 5 \\[1.5ex] 2x+3y-z = 4\end{cases}$

المصفوفة A والمصفوفة الموسعة A’ للنظام هما:

$\displaystyle A= \left( \begin{array}{ccc} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & -1 & 2 & 1 \\[1.1ex] 3 & 2 & 1 & 5 \\[1.1ex] 2 & 3 & -1 & 4 \end{array} \right)$

نحسب الآن رتبة المصفوفة A. للقيام بذلك، نتحقق مما إذا كان محدد المصفوفة بأكملها مختلفًا عن 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{vmatrix} = 0$

محدد المصفوفة A بأكملها يعطي 0، لذا فهي ليست من الرتبة 3. لمعرفة ما إذا كانت من الرتبة 2، يجب أن نجد مصفوفة فرعية في A محددها مختلف عن 0. على سبيل المثال، ذلك من الزاوية اليسرى العليا :

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

نظرًا لأن المصفوفة لها محدد 2 × 2 يختلف عن 0، فإن المصفوفة A لها المرتبة 2:

$\displaystyle rg(A)=2$

بمجرد أن نعرف رتبة “أ”، فإننا نحسب رتبة “أ”. نحن نعلم بالفعل أن محدد الأعمدة الثلاثة الأولى يعطي 0، لذلك جربنا المحددات الأخرى الممكنة 3×3:

$\displaystyle \begin{vmatrix}1 & -1 & 1 \\[1.1ex] 3 & 2 & 5 \\[1.1ex] 2 & 3 & 4\end{vmatrix} = 0 \quad \begin{vmatrix}1 & 2 & 1 \\[1.1ex] 3 & 1 & 5 \\[1.1ex] 2 & -1 & 4\end{vmatrix} = 0 \quad \begin{vmatrix} -1 & 2 & 1 \\[1.1ex] 2 & 1 & 5 \\[1.1ex] 3 & -1 & 4\end{vmatrix} = 0$

جميع المحددات 3×3 للمصفوفة A’ هي 0، وبالتالي فإن المصفوفة A’ لن تكون في المرتبة 3 أيضًا. ومع ذلك، بداخله محددات للترتيب 2 تختلف عن 0. على سبيل المثال:

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

وبالتالي فإن المصفوفة A’ ستكون من المرتبة 2 :

$\displaystyle rg(A')=2$

مدى المصفوفة A يساوي مدى المصفوفة A’ لكن هذه أقل من عدد المجهولات في النظام (3). لذلك، وفقًا لنظرية روشيه-فروبينيوس، فهو نظام متوافق غير محدد (ICS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

مثال لنظام غير متوافق (IS)

$\begin{cases} 2x+y-2z=3 \\[1.5ex] 3x-2y+z= 2 \\[1.5ex] x+4-5z = 3 \end{cases}$

المصفوفة A والمصفوفة الموسعة A’ للنظام هما:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -2 & 3 \\[1.1ex] 3 & -2 & 1 & 2 \\[1.1ex] 1 & 4 & -5 & 3 \end{array} \right)$

نحسب الآن رتبة المصفوفة A. للقيام بذلك، نتحقق مما إذا كان محدد المصفوفة بأكملها مختلفًا عن 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & -2 \end{vmatrix} = -7 \neq 0$

بما أن المصفوفة لها محدد من الرتبة 2 يختلف عن 0، فإن المصفوفة A من الرتبة 2:

$\displaystyle rg(A)=2$

بمجرد أن نعرف رتبة “أ”، فإننا نحسب رتبة “أ”. نحن نعلم بالفعل أن محدد الأعمدة الثلاثة الأولى يعطي 0، لذلك نحاول الآن، على سبيل المثال، مع محدد الأعمدة الثلاثة الأخيرة:

$\displaystyle \begin{vmatrix} 1 & -2 & 3 \\[1.1ex] -2 & 1 & 2 \\[1.1ex] 4 & -5 & 3 \end{vmatrix} = 3 \neq 0$

من ناحية أخرى، تحتوي المصفوفة A’ على محدد نتيجته مختلفة عن 0، وبالتالي فإن المصفوفة A’ سيكون لها المرتبة 3 :

$\displaystyle rg(A')=3$

لذلك، بما أن رتبة المصفوفة A أصغر من رتبة المصفوفة A’، فإننا نستنتج من نظرية Rouché-Frobenius أنه نظام غير متوافق (SI) :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

حل مسائل نظرية روشيه-فروبينيوس

التمرين 1

حدد نوع نظام المعادلات التالي ذو الثلاثة مجاهيل باستخدام نظرية روشيه-فروبينيوس:

انظر الحل

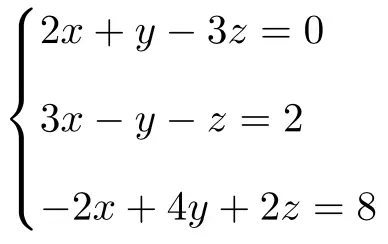
نقوم أولاً بإنشاء المصفوفة A والمصفوفة الموسعة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 3 & -1 & -1 & 2 \\[1.1ex] -2 & 4 & 2 & 8 \end{array} \right)$

يجب علينا الآن العثور على رتبة المصفوفة A. للقيام بذلك، نتحقق مما إذا كان محدد المصفوفة مختلفًا عن 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{vmatrix} = -4+2-36+6+8-6=-30 \bm{\neq 0}$

المصفوفة التي لها محدد من الدرجة الثالثة يختلف عن 0، المصفوفة A لها المرتبة 3:

$\displaystyle rg(A)=3$

بمجرد أن نعرف رتبة “أ”، فإننا نحسب رتبة “أ”. سيكون هذا على الأقل من الرتبة 3، لأننا رأينا للتو أنه يحتوي داخل محدد من الرتبة 3 يختلف عن 0. علاوة على ذلك، لا يمكن أن يكون من الرتبة 4، لأننا لا نستطيع عدم إنشاء محدد 4×4. ولذلك، فإن المصفوفة A’ هي أيضًا من المرتبة 3:

$\displaystyle rg(A')=3$

وبالتالي، وبفضل نظرية روشيه-فروبينيوس، نعلم أنه نظام متوافق محدد (SCD)، لأن مدى A يساوي نطاق A’ وعدد المجهولين.

تمرين 2

صنف نظام المعادلات التالي ذو الثلاثة مجاهيل باستخدام نظرية روشيه-فروبينيوس:

انظر الحل

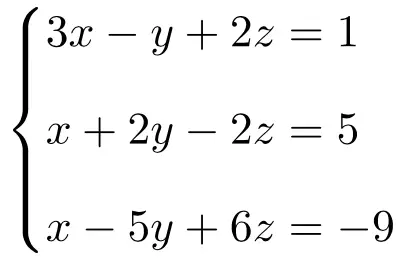
نقوم أولاً ببناء المصفوفة A والمصفوفة الموسعة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc}3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -1 & 2 & 1 \\[1.1ex] 1 & 2 & -2 & 5 \\[1.1ex] 1 & -5 & 6 & -9 \end{array} \right)$

الآن دعونا نحسب مدى المصفوفة A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 3 & -1 \\[1.1ex] 1 & 2 \end{vmatrix} = 7 \neq 0$

إذن المصفوفة A لها المرتبة 2:

$\displaystyle rg(A)=2$

$\displaystyle \begin{vmatrix}-1 & 2 & 1 \\[1.1ex] 2 & -2 & 5 \\[1.1ex] -5 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix}3 & 2 & 1 \\[1.1ex] 1 & -2 & 5 \\[1.1ex] 1 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix} 3 & -1 & 1 \\[1.1ex] 1 & 2 & 5 \\[1.1ex] 1 & -5 & -9\end{vmatrix} = 0$

جميع المحددات 3×3 للمصفوفة A’ هي 0، وبالتالي فإن المصفوفة A’ لن تكون في المرتبة 3 أيضًا. إلا أن بداخله محددات كثيرة للترتيب 2 تختلف عن 0. على سبيل المثال:

$\displaystyle \begin{vmatrix} -1 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -2 \neq 0$

وبالتالي فإن المصفوفة A’ ستكون من المرتبة 2 :

$\displaystyle rg(A')=2$

رتبة المصفوفة A تساوي رتبة المصفوفة A’ لكن هاتين الرتبتين أقل من عدد المجهولات في النظام (3). لذلك، من خلال نظرية Rouché-Frobenius نعلم أنه نظام متوافق غير محدد (ICS):

التمرين 3

حدد نوع النظام الذي يستخدم فيه نظام المعادلات التالي نظرية روشيه-فروبينيوس:

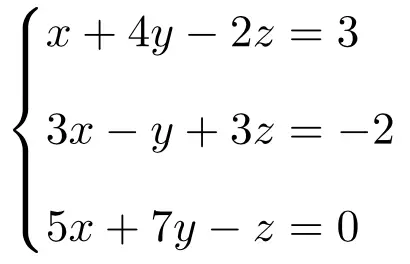
تمرين تم حله خطوة بخطوة لنظرية روش - فروبينيوس

انظر الحل

نقوم أولاً بإنشاء المصفوفة A والمصفوفة الموسعة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 4 & -2 & 3 \\[1.1ex] 3 & -1 & 3 & -2 \\[1.1ex] 5 & 7 & -1 & 0 \end{array} \right)$

الآن دعونا نحسب مدى المصفوفة A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 1 & 4 \\[1.1ex] 3 & -1 \end{vmatrix} = -13 \neq 0$

إذن المصفوفة A لها المرتبة 2:

$\displaystyle rg(A)=2$

بمجرد أن نعرف رتبة “أ”، فإننا نحسب رتبة “أ”. نحن نعلم بالفعل أن محدد الأعمدة الثلاثة الأولى يعطي 0، ولكن ليس محدد الأعمدة الثلاثة الأخيرة:

$\displaystyle \begin{vmatrix} 4 & -2 & 3 \\[1.1ex]-1 & 3 & -2 \\[1.1ex] 7 & -1 & 0 \end{vmatrix} = -40 \neq 0$

لذلك فإن المصفوفة A’ لها المرتبة 3 :

$\displaystyle rg(A')=3$

رتبة المصفوفة A أصغر من رتبة المصفوفة A’، وبالتالي يمكننا أن نستنتج من نظرية Rouché-Frobenius أنه نظام غير متوافق (SI) :

التمرين 4

حدد نوع نظام المعادلات التالي ذو الثلاثة مجاهيل باستخدام نظرية روشيه-فروبينيوس:

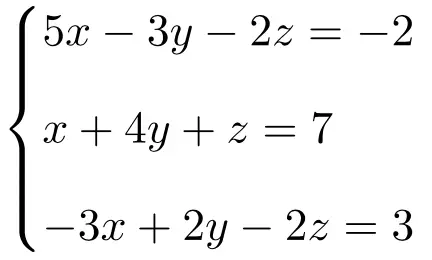
روش - حل تمرين بنظرية فروبينيوس مع 3 مجاهيل و3 معادلات

انظر الحل

نقوم أولاً بإنشاء المصفوفة A والمصفوفة الموسعة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 5 & -3 & -2 & -2 \\[1.1ex] 1 & 4 & 1 & 7 \\[1.1ex]-3 & 2 & -2 & 3 \end{array} \right)$

يجب علينا الآن حساب رتبة المصفوفة A. وللقيام بذلك، نحل محدد المصفوفة باستخدام قاعدة ساروس:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{vmatrix} = -40+9-4-24-10-6=-75 \bm{\neq 0}$

المصفوفة التي لها محدد من الدرجة الثالثة يختلف عن 0، المصفوفة A لها المرتبة 3:

$\displaystyle rg(A)=3$

لذلك، فإن المصفوفة A’ هي أيضًا من الرتبة 3 ، نظرًا لأنها دائمًا على الأقل من الرتبة A ولا يمكن أن تكون من الرتبة 4 لأننا لا نستطيع حل أي محدد 4×4.

$\displaystyle rg(A')=3$

وهكذا، وبفضل تطبيق نظرية روشيه-فروبينيوس، نعلم أن النظام هو نظام محدد متوافق (SCD)، لأن مدى A يساوي نطاق A’ وعدد المجهولين.

التمرين 5

حدد نوع النظام الذي يستخدم فيه نظام المعادلات التالي نظرية روشيه-فروبينيوس:

انظر الحل

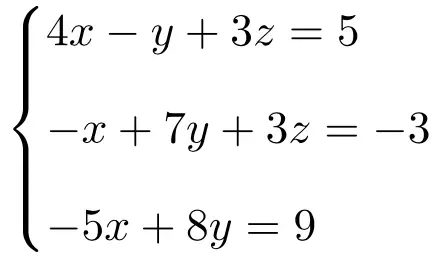
نقوم أولاً بإنشاء المصفوفة A والمصفوفة الموسعة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 3 & 5 \\[1.1ex] -1 & 7 & 3 & -3 \\[1.1ex] -5 & 8 & 0 & 9 \end{array} \right)$

الآن دعونا نحسب مدى المصفوفة A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 4 & -1 \\[1.1ex] -1 & 7 \end{vmatrix} = 27 \neq 0$

وبالتالي فإن المصفوفة A هي في المرتبة 2:

$\displaystyle rg(A)=2$

بمجرد أن نعرف رتبة “أ”، فإننا نحسب رتبة “أ”. محدد الأعمدة الثلاثة الأولى التي نعرفها بالفعل يعطي 0، لكن محدد الأعمدة الثلاثة الأخيرة لا يعطي:

$\displaystyle \begin{vmatrix} -1 & 3 & 5 \\[1.1ex] 7 & 3 & -3 \\[1.1ex] 8 & 0 & 9\end{vmatrix} = -408 \neq 0$

وبالتالي فإن المصفوفة A’ لها المرتبة 3 :

$\displaystyle rg(A')=3$

وأخيرًا، نطبق المجال على نظرية روشيه-فروبينيوس: مجال المصفوفة A أصغر من مجال المصفوفة A’، وبالتالي فهو نظام غير متوافق (SI) :

التمرين 6

صنف نظام المعادلات التالي من الرتبة 3 باستخدام نظرية روشيه-فروبينيوس:

$\begin{cases} 6x-2y+4z=1 \\[1.5ex] -2x+4y+3z= 7 \\[1.5ex] 8x-6y+z = -6\end{cases}$

انظر الحل

نقوم أولاً ببناء المصفوفة A والمصفوفة الموسعة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 6 & -2 & 4 & 1 \\[1.1ex] -2 & 4 & 3 & 7 \\[1.1ex] 8 & -6 & 1 & -6 \end{array} \right)$

الآن دعونا نحسب مدى المصفوفة A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

إذن المصفوفة A لها المرتبة 2:

$\displaystyle rg(A)=2$

بمجرد أن نعرف رتبة “أ”، نقوم بحساب رتبة “أ”. نحن نعلم بالفعل أن محدد الأعمدة الثلاثة الأولى يعطي 0، لذلك جربنا المحددات الأخرى الممكنة 3×3:

$\displaystyle \begin{vmatrix} -2 & 4 & 1 \\[1.1ex]4 & 3 & 7 \\[1.1ex] -6 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix}6 & 4 & 1 \\[1.1ex] -2 & 3 & 7 \\[1.1ex] 8 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix} 6 & -2 & 1 \\[1.1ex] -2 & 4 & 7 \\[1.1ex] 8 & -6 & -6\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

وبالتالي فإن المصفوفة A’ ستكون من المرتبة 2 :

$\displaystyle rg(A')=2$

أخيرًا، من خلال تطبيق نظرية روشيه-فروبينيوس، نعلم أنه نظام متوافق غير محدد (ICS)، لأن مدى المصفوفة A يساوي مدى المصفوفة A’ لكن هاتين المصفوفتين أصغر من عدد المجهولات في النظام (3):

ما هي نظرية روشيه-فروبينيوس؟

بيان نظرية روشيه-فروبينيوس

مثال على النظام المتوافق المحدد (SCD)

مثال على نظام متوافق غير محدد (ICS)

مثال لنظام غير متوافق (IS)

حل مسائل نظرية روشيه-فروبينيوس

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

التمرين 6

اترك تعليقاً إلغاء الرد