نظرية العامل

في هذه الصفحة نشرح ما هي نظرية العامل. بالإضافة إلى ذلك، نعرض الغرض من استخدام نظرية العوامل: قسمة كثيرات الحدود، وإيجاد الجذور، وتحليل كثيرات الحدود إلى عوامل، وما إلى ذلك. وأخيرًا، سوف تكون قادرًا على التدرب على نظرية العوامل خطوة بخطوة.

ما هي نظرية العامل؟

في الرياضيات، تقول نظرية العوامل أن كثيرة الحدود P(x) قابلة للقسمة على كثيرة حدود أخرى من الشكل (xa) إذا وفقط إذا كانت P(a)=0.

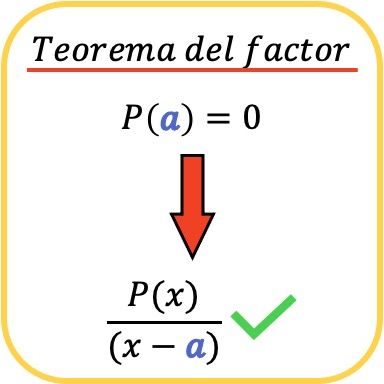
وبالمثل، نتيجة لنظرية العامل، يترتب على ذلك أنه إذا كانت كثيرة الحدود P(x) قابلة للقسمة على المصطلح (x−a)، فهذا يعني أن القيمة a هي جذر (أو صفر) لكثيرة الحدود P( x ) .

أن تكون كثيرة الحدود قابلة للقسمة على أخرى، مما يعني أن باقي (أو باقي) القسمة بين كثيرتي الحدود يساوي صفرًا. في حال كنت لا تتذكر هذا المفهوم بالكامل، في الرابط التالي يمكنك مشاهدة أمثلة على تقسيم كثيرات الحدود ، وهناك ستجد أيضًا شرحًا لكيفية قسمة كثيرات الحدود وتمارين محلولة خطوة بخطوة.

أمثلة على نظرية العامل

الآن بعد أن عرفنا التعريف الرياضي لنظرية العامل، دعونا نلقي نظرة على عدة أمثلة لنرى كيف يتم تطبيقها.

مثال 1

أحد تطبيقات نظرية العامل هو معرفة ما إذا كانت كثيرة حدود معينة قابلة للقسمة على ذات الحدين . دعونا نرى مثالاً لكيفية القيام بذلك باستخدام نظرية العامل:

حدد ما إذا كانت كثيرة الحدود P(x) قابلة للقسمة على ذات الحدين Q(x)، وكلاهما:

$P(x)=x^2-4x+3 \qquad \qquad Q(x)=x-1$

أولاً، كثيرة الحدود المقسوم عليها، Q(x)، هي كثيرة الحدود من النوع (xa)، لذا يمكننا تطبيق نظرية العامل لحل المشكلة.

لذلك، للتحقق مما إذا كان من الممكن قسمة P(x) على Q(x)، نحتاج إلى حساب القيمة العددية لكثيرة الحدود P(x) لـ x=1، نظرًا لأن 1 هو الحد المستقل لكثيرة الحدود المقسومة مع تغيير إشارتها :

$\begin{aligned} P(1) & =1^2-4\cdot 1+3 \\[2ex] & = 1-4+3 \\[2ex] & = 0 \end{aligned}$

القيمة العددية لمتعددة الحدود P(x) عند x = 1 تعطي صفرًا، لذلك وفقًا لنظرية العامل P(x) قابلة للقسمة على Q(x)، أو بمعنى آخر، فإن باقي القسمة على كليهما سيكون فارغًا.

يمكننا التحقق من استيفاء شرط القسمة عن طريق قسمة كثيرتي الحدود على نظرية روفيني :

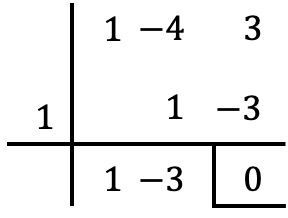
كما ترون في هذا المثال، نظرية العامل هي حالة خاصة من نظرية الباقي (أو الباقي). أترك لك هذا المقال الذي يشرح ما هي نظرية الباقي ، وستجد أيضًا أمثلة وتمارين تم حلها بها. والأكثر من ذلك، أنك سوف تكون قادرًا على رؤية الفرق بين نظرية الباقي ونظرية العامل.

مثال 2

يمكن أيضًا استخدام نظرية العوامل للعثور على جذور (أو أصفار) كثيرة الحدود. لكن، من الواضح، لفهم هذا النوع من المسائل، عليك أن تعرف ما هي جذور كثيرة الحدود . إذا كنت لا تزال لا تفهم هذا المفهوم، فيمكنك إلقاء نظرة على الصفحة المرتبطة، والتي تم شرحها بالتفصيل.

لذلك دعونا نرى من خلال مثال كيفية تطبيق نظرية العامل للعثور على جذر كثيرة الحدود:

بالنظر إلى كثيرة الحدود P(x)، احسب إذا كان أحد جذورها x=2:

$P(x)=x^3-3x^2+5x-6$

بتطبيق نظرية العامل، فإن المصطلح x=2 سيكون جذرًا لكثيرة الحدود P(x) فقط إذا كانت القيمة العددية لـ P(x) لـ x=2 هي صفر. لذا علينا إيجاد هذه القيمة العددية:

$\begin{aligned} P(2) & =2^3-3\cdot 2^2+5\cdot 2-6 \\[2ex] & = 8-3\cdot 4 +5\cdot 2 -6\\[2ex] & = 8-12+10-6 \\[2ex] & = 0\end{aligned}$

في الواقع، القيمة العددية لكثيرة الحدود P(x) تختفي عند x=2، لذا بفضل نظرية العامل يمكننا التأكيد على أن x=2 هو جذر لكثيرة الحدود P(x).

تحليل كثيرات الحدود إلى عوامل باستخدام نظرية العامل

تطبيق آخر لنظرية العامل هو تحليل كثيرات الحدود . في حال كنت لا تعرف ما هو، فإن تحليل كثيرة الحدود يعني تحويل تعبير كثيرة الحدود إلى حاصل ضرب العوامل، أي أن تحليل كثيرة الحدود يبسط تعبيرها الجبري.

وبالتالي، تنص النظرية العاملية على أنه إذا كانت كثيرة الحدود P(x) تحقق P(a)=0 لقيمة معينة a، فيمكن تحليل التعبير عن كثيرة الحدود المذكورة إلى المنتج P(x)=(xa)·Q( x)، حيث Q(x) هو كثير الحدود الناتج عن قسمة كثير الحدود P(x) على (xa).

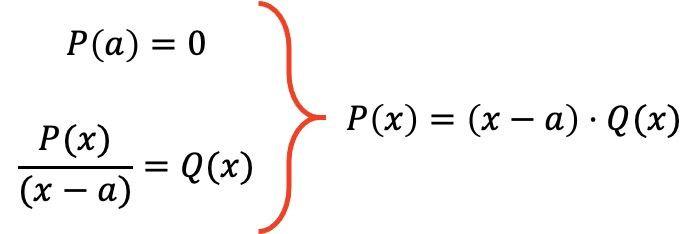
على سبيل المثال، سنقوم بتحليل كثيرة الحدود التالية باستخدام النظرية المضروب:

$P(x)=x^3+2x^2+4x+8$

من كثيرة الحدود السابقة يمكننا أن نعرف أن x=-2 هو أحد جذورها، حيث أن القيمة العددية لكثيرة الحدود x=-2 تساوي صفر:

$\begin{aligned} P(-2) & =(-2)^3+2\cdot (-2)^2+4\cdot (-2)+8 \\[2ex] & =-8+2\cdot 4+4\cdot (-2)+8 \\[2ex] & = -8+8-8+8 \\[2ex] & = 0 \end{aligned}$

ولذلك فإننا نقسم مع قاعدة روفيني كثيرة الحدود P(x) بين ذات الحدين التي شكلتها x وعلامة تغير الجذر، أي العامل (x+2):

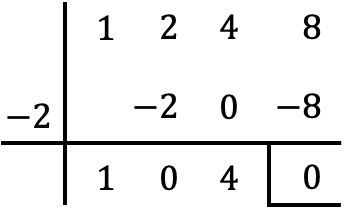
وبالتالي فإن حاصل قسمة كثيرات الحدود هو:

$\cfrac{P(x)}{x+2} =x^2+4$

وأخيرًا، من خلال نظرية العامل، يمكننا التعبير عن كثيرة الحدود P(x) في شكل ضرب العامل (x+2) في حاصل القسمة السابقة:

$P(x) = (x+2) \cdot (x^2+4)$

لقد قمنا بالتالي بتحليل متعدد الحدود P(x)، ولكن جزئيًا فقط. من أجل تحليل كثير الحدود بشكل كامل، يجب تطبيق إجراء أطول. لقد قمنا بإعداد دليل حيث نعلم خطوة بخطوة كيفية تحليل كثيرات حدود روفيني إلى عوامل ، بالإضافة إلى ذلك، قمنا في هذه المقالة بشرح جميع أنواع التحليلات وستكون قادرًا على التدرب على التمارين التي تم حلها. لذا انقر فوق الرابط لمعرفة كيفية تحليل كثيرة الحدود من المجموعة.

مسائل نظرية العوامل المحلولة

بعد ذلك، قمنا بإعداد العديد من التمارين التي تم حلها خطوة بخطوة حول نظرية العوامل حتى تتمكن من التدرب عليها، وبالتالي التحقق مما إذا كنت قد فهمت هذه النظرية. نوصي بمحاولة القيام بذلك بنفسك ثم معرفة ما إذا كنت تفهم الحل بشكل صحيح. ولا تنسوا أيضًا أنه يمكنكم ترك أسئلتكم أدناه في التعليقات! ❓❓💬💬

التمرين 1

استخدم النظرية العاملية لمعرفة ما إذا كانت كثيرة الحدود P(x) قابلة للقسمة على ذات الحدين Q(x)، وإذا كان الأمر كذلك، ابحث عن جذر كثيرة الحدود وقم بتحليلها.

$P(x)=2x^3-4x^2+x-7 \qquad \qquad Q(x)=x-3$

انظر الحل

في هذه الحالة، المقسوم عليه كثير الحدود Q(x) هو ذو حدين يتكون فقط من x ومصطلح مستقل. لذا لإظهار أنه يمكن قسمة كثير الحدود P(x) على كثير الحدود الآخر Q(x) باستخدام نظرية العامل، يجب علينا تقييم القيمة العددية لكثير الحدود P(x) في الحد المستقل لعلامة كثير الحدود المقسوم عليها، وهذا يعني عند x=3:

$\begin{aligned} P(3) & =2\cdot 3^3-4\cdot 3^2+3-7\\[2ex] & = 2\cdot 27-4\cdot 9+3-7 \\[2ex] & = 54-36+3-7\\[2ex] & = 14 \end{aligned}$

القيمة العددية للكثيرة الحدود P(x) عند x=3 تعادل 14، أي أنها تختلف عن الصفر. لذلك، وفقًا لنظرية العامل، P(x) غير قابلة للقسمة على Q(x) لأن باقي القسمة ليس صفرًا.

تمرين 2

اكتشف من خلال النظرية العاملية ما إذا كانت كثيرة الحدود P(x) قابلة للقسمة على ذات الحدين Q(x)، وإذا كان الأمر كذلك، فابحث عن جذر كثيرة الحدود P(x) وقم بتحليلها.

$P(x)=x^3+5x^2+3x-1 \qquad \qquad Q(x)=x+1$

انظر الحل

في هذه الحالة، المقسوم عليه كثير الحدود Q(x) هو ذو حدين يتكون فقط من x ومصطلح مستقل، وبالتالي يمكننا تطبيق نظرية المضروب.

وللتحقق مما إذا كان يمكن قسمة كثير الحدود P(x) على كثير الحدود Q(x)، يجب أن نجد القيمة العددية لكثير الحدود P(x) للحد المستقل للعلامة المتغيرة متعدد الحدود Q(x)، فهي أي عند x=-1:

$\begin{aligned} P(-1) & =(-1)^3+5\cdot (-1)^2+3\cdot (-1)-1\\[2ex] & = -1+5\cdot 1+3\cdot (-1)-1\\[2ex] & = -1+5-3-1\\[2ex] & = 0 \end{aligned}$

في هذه المشكلة، القيمة العددية لكثيرة الحدود عند x=-1 هي صفر، لذا فإن P(x) قابلة للقسمة على Q(x).

بعد ذلك، يمكننا أن نستنتج من خلال النظرية المضروب أن x=-1 هو جذر متعدد الحدود P(x)، حيث أن القيمة العددية لـ P(x) عند x=-1 تختفي.

وبالتالي، بما أن x=-1 هو جذر كثيرة الحدود P(x)، لتحليلها، قم ببساطة بتقسيمها على x+1. ولهذا سنستخدم طريقة روفيني:

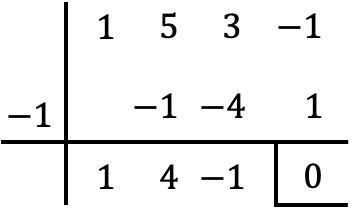
وبالتالي فإن نتيجة العملية هي:

$x^2+4x-1$

وبالتالي يمكننا تحليل متعدد الحدود P(x) على النحو التالي:

$P(x) = (x+1) \cdot (x^2+4x-1)$

التمرين 3

اكتشف باستخدام النظرية العاملية ما إذا كانت كثيرة الحدود P(x) قابلة للقسمة على ذات الحدين Q(x)، وإذا كان الأمر كذلك، فابحث أيضًا عن جذر كثيرة الحدود P(x) وقم بتحليلها.

$P(x)=x^3+5x^2+4x-6 \qquad \qquad Q(x)=x+3$

انظر الحل

في هذه الحالة، كثيرة الحدود التي تقسم Q(x) هي ذات حدين مكونة فقط من x ومصطلح مستقل، لذلك يمكننا استخدام نظرية العامل.

وللتحقق مما إذا كان كثير الحدود P(x) قابلاً للقسمة على كثير الحدود Q(x)، يجب علينا تحديد القيمة العددية لكثير الحدود P(x) للمصطلح المستقل للعلامة المتغيرة متعدد الحدود Q(x)، أي- أي عند x =-3:

$\begin{aligned} P(-3) & =(-3)^3+5\cdot (-3)^2+4\cdot (-3)-6\\[2ex] & = -27+5\cdot 9+4\cdot (-3)-6\\[2ex] & = -27+45-12-6\\[2ex] & = 0 \end{aligned}$

في هذه الحالة، القيمة العددية لكثيرة الحدود عند x=-3 هي صفر، وبالتالي فإن P(x) قابلة للقسمة على Q(x).

لهذا السبب، نستنتج من النظرية العاملية أن x=-3 هو جذر متعدد الحدود P(x)، حيث أن P(-3) يساوي الصفر.

لذا، بما أن x=-3 هو جذر كثيرة الحدود P(x)، فلتحليلها يجب أن نقسمها على x+3. ولهذا سوف نستخدم قاعدة روفيني:

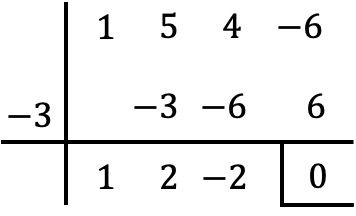
إذن نتيجة القسمة هي:

$x^2+2x-2$

وبالتالي، يمكننا تحليل كثيرة الحدود P(x) بالطريقة التالية:

$P(x) = (x+3) \cdot (x^2+2x-2)$

ما رأيك في نظرية العامل؟ هل تعتقد أنه مفيد في الجبر؟ نقرأ لك في التعليقات!
👀⬇⬇⬇👀

ما هي نظرية العامل؟

أمثلة على نظرية العامل

مثال 1

مثال 2

تحليل كثيرات الحدود إلى عوامل باستخدام نظرية العامل

مسائل نظرية العوامل المحلولة

التمرين 1

تمرين 2

التمرين 3

اترك تعليقاً إلغاء الرد