نظام الإحداثيات

نشرح في هذه الصفحة ما هو نظام الإحداثيات، وبالإضافة إلى ذلك، ستجد كل شيء عن نظام الإحداثيات الديكارتية. ستشاهد أيضًا أنواعًا أخرى من أنظمة الإحداثيات (القطبية، الأسطوانية، الكروية، إلخ) والتطبيقات الواقعية لنظام الإحداثيات.

ما هو نظام الإحداثيات؟

على الرغم من صعوبة فهم هذا المفهوم في البداية، إلا أن تعريف نظام الإحداثيات هو:

نظام الإحداثيات هو نظام يسمح لنا بتحديد موضع نقطة ما. أي أنها مجموعة من القيم المستخدمة لتحديد موقع أي كائن هندسي.

على سبيل المثال، يمكن وصف الموقع الذي تحلق فيه الطائرة التالية بواسطة نظام الإحداثيات:

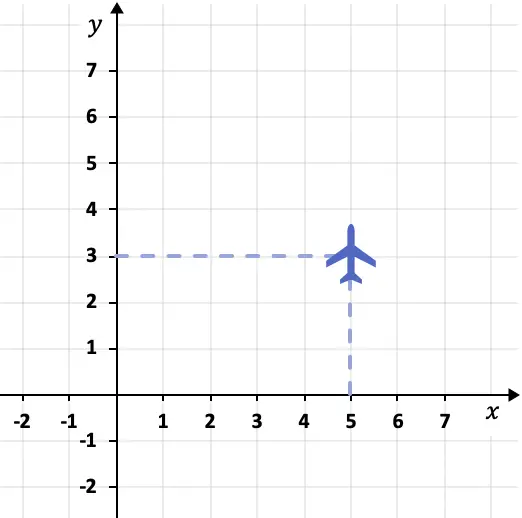
وفي هذه الحالة يكون المستوى عند النقطة (5.3). لأن إحداثي X هو 5 وإحداثي Y هو 3.

$(5,3)$

ومن ناحية أخرى، تسمى النقطة (0,0) بأصل الإحداثيات ، لأنها تبدأ منها محاور الإحداثيات وهي النقطة المرجعية لنظام الإحداثيات.

ومن باب الفضول يعتبر أن عالم الرياضيات الذي اخترع نظام الإحداثيات هو الفرنسي رينيه ديكارت. ولهذا السبب يطلق عليه أيضًا نظام الإحداثيات الديكارتية.

نظام الإحداثيات الديكارتية في المستوى

الرسم البياني الذي رأيناه في القسم السابق ينتمي إلى نظام الإحداثيات الديكارتية في المستوى. ونقول أنه في المستوى لأنه نظام ثنائي الأبعاد، أي أن له محورين فقط: المحور X والمحور Y.

يتوافق المحور X مع الإحداثيات الأفقية، بينما يمثل المحور Y الإحداثيات الرأسية. أدناه يمكنك رؤية عدة نقاط ممثلة بيانيا مع إحداثياتها:

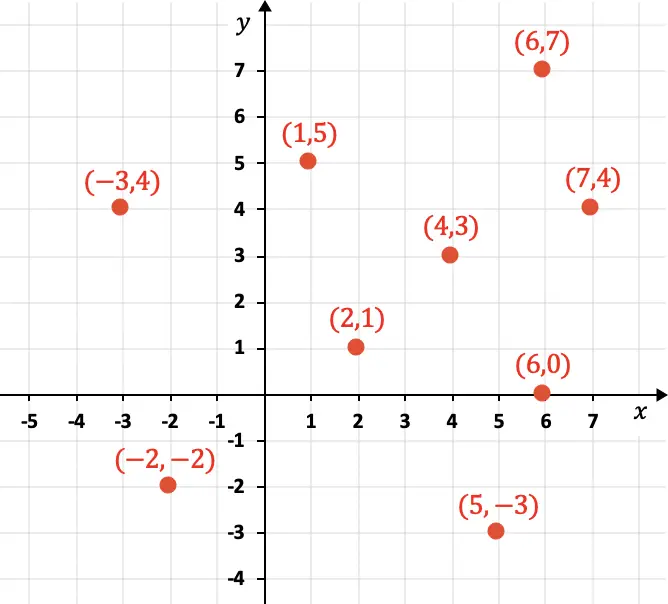
وكما ترون في الرسم البياني، يتم تمثيل الإحداثيات عددياً بين قوسين، بالإضافة إلى ذلك يتم وضع المكون X أولاً ومن ثم المكون Y: (4،3). بالإضافة إلى ذلك، يمكن أن تكون الإحداثيات موجبة أو سالبة أو صفرًا.

ومن ناحية أخرى، يُسمى هذا النوع من نظام الإحداثيات أيضًا بالمستوى الديكارتي.

وأخيرًا، يجب أن تعلم أنه يمكن قول المحاور الإحداثية بعدة طرق، على الرغم من أنها جميعًا تعني نفس الشيء:

يُطلق على المحور X أيضًا اسم محور الإحداثي السيني أو محور OX.
يُسمى المحور Y أيضًا بالمحور y أو محور OY.

نظام الإحداثيات الديكارتية في الفضاء

لقد رأينا للتو كيفية تمثيل نقطة في المستوى، أي في نظام إحداثي ذي محورين (بعدين). لكن الواقع يتكون من ثلاثة أبعاد (الارتفاع والعرض والعمق).

وهكذا، في الهندسة الإقليدية، يتم تمثيل الفضاء ثلاثي الأبعاد بشكل عام بواسطة نظام إحداثي ذو ثلاثة محاور، جميعها متعامدة مع بعضها البعض:

يمثل المحور X العمق.
يشير المحور Y إلى العرض.
المحور Z يتوافق مع الارتفاع.

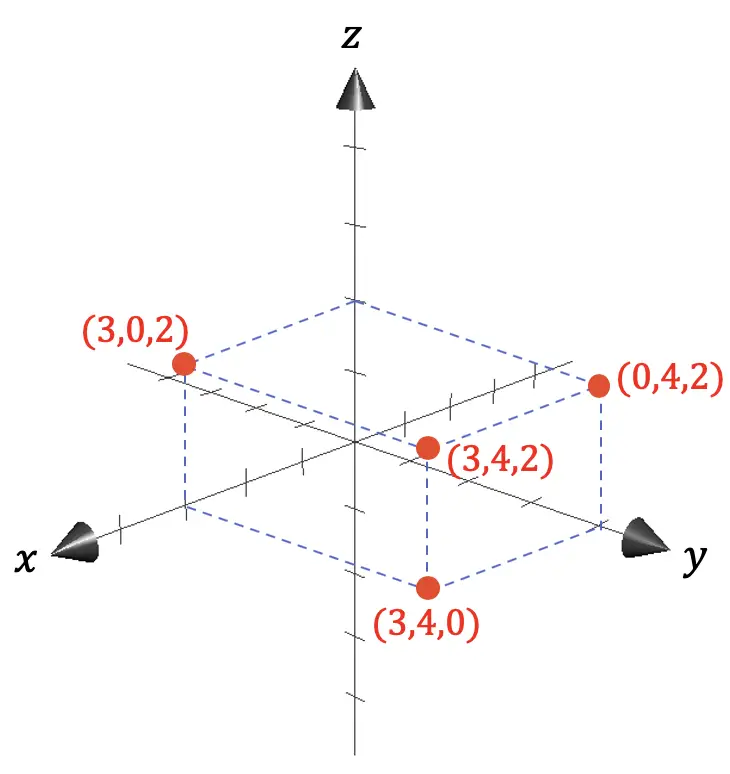
نظام الإحداثيات الديكارتية في الفضاء ثلاثي الأبعاد

كما ترون في التمثيل البياني السابق، يتم إعطاء إحداثيات أي نقطة من خلال الإسقاطات على محاور المسافات بين النقطة المعنية ونقطة الأصل (0،0،0).

نظام الإحداثيات القطبية

أنظمة الإحداثيات الديكارتية، ثنائية أو ثلاثية الأبعاد، هي الأكثر استخدامًا. لكن في بعض المناسبات قد يكون من المناسب لنا استخدام نوع آخر من نظام الإحداثيات.

نظام الإحداثيات القطبية هو نظام مرجعي ثنائي الأبعاد إحداثياته هي:

$\bm{r}$

هي المسافة بين أصل الإحداثيات والنقطة. وهذا ما يسمى الإحداثيات الشعاعية.
$\bm{\theta}$

هي الزاوية التي يصنعها المحور X مع الخط الذي يمر عبر النقطة ونقطة الأصل. وهذا ما يسمى الإحداثيات الزاوي أو السمتي.

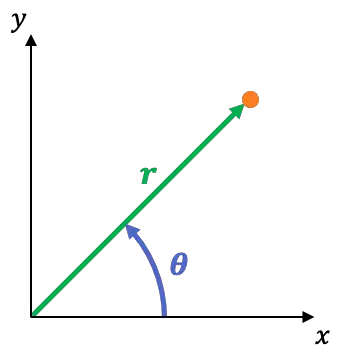
يمكنك التبديل بسهولة من نظام الإحداثيات المستطيل إلى نظام الإحداثيات القطبية باستخدام المعادلات التالية:

تحويل الإحداثيات القطبية إلى الإحداثيات الديكارتية

$x=r\cdot\text{cos}(\theta)$

$y=r\cdot\text{sen}(\theta)$

التحول من الإحداثيات الديكارتية إلى الإحداثيات القطبية

$r= \sqrt{x^2+y^2}$

$\displaystyle \theta = \text{arctan}\left(\frac{y}{x}\right)$

نظام الإحداثيات الأسطواني

نظام الإحداثيات الأسطواني يشبه إلى حد كبير نظام الإحداثيات القطبية. في الواقع، إنه نفس الشيء ولكن بإحداثيات أخرى: الارتفاع.

وبالتالي فإن الإطار الأسطواني هو إطار ثلاثي الأبعاد، أي بثلاثة إحداثيات:

$\bm{r}$

هو الإسقاط المتعامد للنقطة في المستوى XY، أو بمعنى آخر مسافة النقطة من المحور Z.
$\bm{\theta}$

هي الزاوية التي نصف المحور الموجب

$r.$
$\bm{z}$

هو ارتفاع النقطة، وهو نفس إحداثيات نظام الإحداثيات الديكارتية في الفضاء.

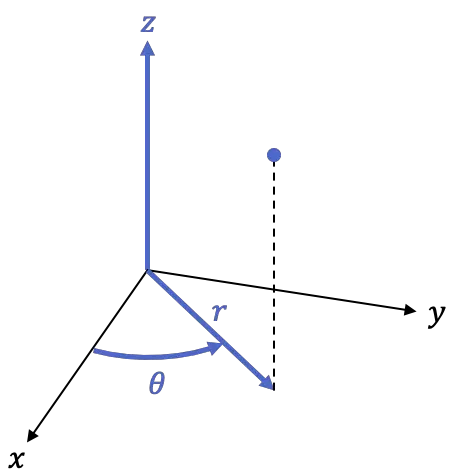
تُستخدم الصيغ التالية لتحويل نظام الإحداثيات الديكارتية إلى إحداثيات أسطوانية:

تحويل الإحداثيات الأسطوانية إلى الإحداثيات الديكارتية

$x=r\cdot\text{cos}(\theta)$

$y=r\cdot\text{sen}(\theta)$

$z = z$

تحويل الإحداثيات الديكارتية إلى الإحداثيات الأسطوانية

$r= \sqrt{x^2+y^2}$

$\displaystyle \theta = \text{arctan}\left(\frac{y}{x}\right)$

$z = z$

نظام الإحداثيات الكروية

وأخيرا، لدينا نظام الإحداثيات الكروية. هذا النوع من نظام الإحداثيات يشبه أيضًا إلى حد كبير الإحداثيات القطبية والإحداثيات الأسطوانية، على الرغم من وجود بعض الاختلافات عنها بوضوح.

نظام الإحداثيات الكروية هو نظام لوصف الفضاءات الإقليدية ثلاثية الأبعاد، ولذلك فهو يحتوي على ثلاث إحداثيات:

$\bm{r}$

هي المسافة (في R3) من الأصل إلى النقطة.
$\bm{\theta}$

هي الزاوية التي يصنعها الجزء الموجب من المحور X مع الخط

$r$

المسقطة في الطائرة XY.
$\bm{\phi}$

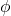
هي الزاوية بين الجزء الموجب للمحور Z والخط

$r.$

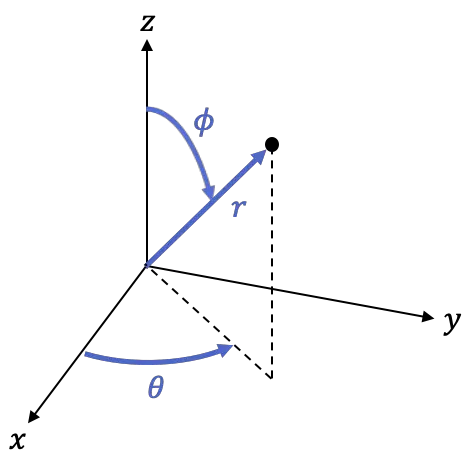
يمكنك التبديل بين الإحداثيات الكروية والديكارتية باستخدام الصيغ التالية:

تحويل الإحداثيات الكروية إلى الإحداثيات الديكارتية

$x=r\cdot\text{cos}(\theta)\cdot\text{sen}(\phi)$

$y=r\cdot \text{sen}(\theta)\cdot\text{sen}(\phi)$

$z = r\cdot\text{cos}(\phi)$

تحويل الإحداثيات الديكارتية إلى إحداثيات كروية

$r= \sqrt{x^2+y^2+z^2}$

$\displaystyle \theta = \text{arctan}\left(\frac{y}{x}\right)$

$\displaystyle \phi = \text{arctan}\left(\frac{\sqrt{x^2+y^2}}{z}\right)$

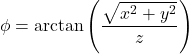
التطبيقات الواقعية لنظام الإحداثيات

تعتبر أنظمة الإحداثيات مهمة جدًا في الرياضيات لأنها تُستخدم أيضًا في الحياة الواقعية. على سبيل المثال، فهي مفيدة لتحديد موقع الأشياء أو الأشخاص أو حتى الأماكن على الخريطة. في الواقع، يوجد نظام تحديد المواقع العالمي (GPS) بسبب أنظمة الإحداثيات، حيث أن هذا هو ما يستخدمونه لمعرفة موقعك على الأرض.

بتعبير أدق، تتكون الإحداثيات الجغرافية لنظام تحديد المواقع العالمي (GPS) من عنصرين: خط العرض وخط الطول. خط العرض (الشمال أو الجنوب) وخط الطول (الشرق أو الغرب) هما إحداثيان زاويان يقيسان الزاوية بين مركز الأرض وموقعك. يتم التعبير عن كلاهما بالدرجات، إما بالإحداثيات العشرية أو الستينية.

ما هو نظام الإحداثيات؟

نظام الإحداثيات الديكارتية في المستوى

نظام الإحداثيات الديكارتية في الفضاء

نظام الإحداثيات القطبية

نظام الإحداثيات الأسطواني

نظام الإحداثيات الكروية

التطبيقات الواقعية لنظام الإحداثيات

اترك تعليقاً إلغاء الرد