ناقلات متحدة المستوى (أو متحدة المستوى)

في هذه الصفحة سوف تتعلم ما هي المتجهات المستوية وكيفية معرفة ما إذا كانت 2، 3، 4 أو أكثر من المتجهات متحدة المستوى. بالإضافة إلى ذلك، ستتمكن من رؤية الأمثلة والتمارين التي تم حلها خطوة بخطوة للمتجهات المستوية.

ما هي ناقلات متحدة المستوى؟

في الهندسة التحليلية، يكون معنى المتجهات المستوية (أو المستوية) كما يلي:

المتجهات المستوية هي ناقلات تنتمي إلى نفس المستوى.

لذلك، يكون المتجهان دائمًا متحدين في المستوى لأنه يمكن تشكيل المستوى باستخدام ما لا يقل عن متجهين. من ناحية أخرى، عندما يكون هناك 3 أو 4 متجهات أو أكثر، فمن الممكن ألا يكون أحد المتجهات موجودًا في نفس المستوى، وبالتالي، لا يكونون متحدين في المستوى.

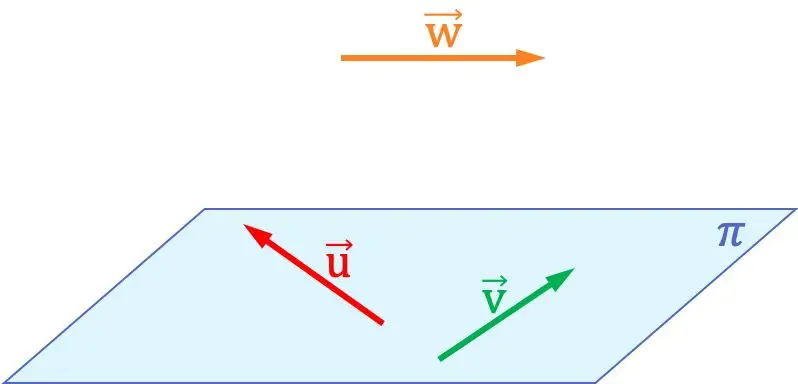
أمثلة على ناقلات متحد المستوى أو متحد المستوى

على سبيل المثال، في الرسم البياني أعلاه يمكنك أن ترى أن المتجهات

$\vv{\text{u}}$

$\vv{\text{v}}$

فهي متحدة المستوى مع بعضها البعض، لأنها موجودة في نفس المستوى. ومن ناحية أخرى، فإن هذين المتجهين ليسا مستويين مع المتجه

$\vv{\text{w}}$

لأنه لا يمكن تشكيل أي مستوى في الفضاء الذي يحتوي على المتجهات الثلاثة.

من هذه الخاصية يمكننا أن نستنتج أنه إذا كانت هناك 3 متجهات أو أكثر متحدة المستوى، فإن النقاط التي تحدد المتجهات المذكورة (بداية ونهاية المتجه) هي أيضًا نقاط مستوية.

متى تكون المتجهات مستوية؟

كما رأينا في تعريف المتجهات متحدة المستوى (أو متحدة المستوى)، فإن المتجهات تكون دائمًا متحدة المستوى، ولكن ليس من الضروري أن يحترم أكثر من متجهين علاقة المستوى المشترك.

وبالتالي، هناك عدة طرق لتحديد ما إذا كانت ثلاثة نواقل أو أكثر متحدة المستوى:

إذا كان حاصل الضرب المختلط لثلاثة متجهات (أو حاصل الضرب الثلاثي) يساوي الصفر، فهذا يعني أن المتجهات الثلاثة متحدة المستوى. إذا لم تكن واضحًا تمامًا بشأن كيفية حساب هذه العملية، أنصحك بإلقاء نظرة على ما هو حاصل الضرب المختلط لثلاثة ناقلات ، ستجد هنا الشرح بالإضافة إلى الأمثلة والتمارين المحلولة.

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] =0$

إذا كان من الممكن التعبير عن مجموعة من المتجهات كمجموعة خطية من متجهين، فهذا يعني أنها متحدة المستوى، مما يعني أن 3 ناقلات أو أكثر تكون متحدة المستوى إذا وفقط إذا كانت معتمدة خطيًا. لإثبات أن ثلاثة متجهات أو أكثر عبارة عن مزيج خطي من متجهين، يكفي أن تكون رتبة المصفوفة التي تشكلها جميع المتجهات تساوي 2.

$rg(A) = 2$

من المهم أن يكون لديك فهم جيد لمفهوم الاعتماد الخطي والاستقلال ، أي عندما يعتمد ناقلان خطيًا أو مستقلان خطيًا وما يعنيه ذلك. إذا لم تكن واضحًا تمامًا، فستجد في الرابط شرحًا مفصلاً للغاية، حيث يمكنك أيضًا مشاهدة الأمثلة والتمارين التي تم حلها خطوة بخطوة.

إذا كانت المتجهات المعنية متجهات متوازية ، فهذا يعني أنها أيضًا مستوية، أي أن جميع المتجهات المتوازية موجودة في نفس المستوى.

$\vv{\text{u}} \parallel \vv{\text{v}} \parallel \vv{\text{w}}$

حل مشاكل المتجهات متحدة المستوى

التمرين 1

حدد ما إذا كانت المتجهات الثلاثة التالية متحدة المستوى:

$\vv{\text{u}} = (3,1,2)$

$\vv{\text{v}} = (2,3,-1)$

$\vv{\text{w}} = (-1,-5,4)$

انظر الحل

للتحقق مما إذا كانت هذه 3 متجهات مستوية، يجب علينا حساب حاصل الضرب المختلط بين المتجهات الثلاثة:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 3 & -1 \\[1.1ex] -1 & -5 & 4 \end{vmatrix} \\[2ex] &= 36+1-20+6-15-8 \\[2ex] & = \bm{0} \end{aligned}$

حاصل الضرب المختلط للمتجهات الثلاثة هو صفر، لذا فإن المتجهات الثلاثة متحدة المستوى .

تمرين 2

حدد ما إذا كانت المتجهات الثلاثة التالية متحدة المستوى:

$\vv{\text{u}} = (4,-2,6)$

$\vv{\text{v}} = (-2,1,-3)$

$\vv{\text{w}} = (6,-3,9)$

انظر الحل

إحدى الطرق للتحقق مما إذا كنا نتعامل مع ثلاثة متجهات مستوية هي إيجاد حاصل الضرب المختلط بين المتجهات الثلاثة. لكن إذا نظرنا جيدًا إلى مركبات المتجهات، فسنلاحظ أنها متناسبة. وبالتالي، فإن المتجهات الثلاثة متوازية مع بعضها البعض.

$\vv{\text{u}} \parallel \vv{\text{v}} \parallel \vv{\text{w}}$

وبما أن جميع المتجهات متوازية، فهي في الواقع 3 متجهات مستوية .

التمرين 3

حدد ما إذا كانت المتجهات الأربعة التالية متحدة المستوى:

$\vv{\text{a}} = (2,1,1)$

$\vv{\text{b}} = (1,-1,2)$

$\vv{\text{c}} = (-1,0,-1)$

$\vv{\text{d}} = (3,1,2)$

انظر الحل

لمعرفة ما إذا كانت المتجهات الأربعة متحدة المستوى، يجب علينا حساب رتبة المصفوفة المكونة من جميع المتجهات:

$\displaystyle A= \begin{pmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{pmatrix}$

في هذه الحالة، نحسب نطاق المصفوفة المذكورة بواسطة المحددات:

$rg(A) = \ ?$

$\displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \end{vmatrix}=0 \quad \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex]3&1&2\end{vmatrix} =0$

$\displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0 \quad \begin{vmatrix} 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0$