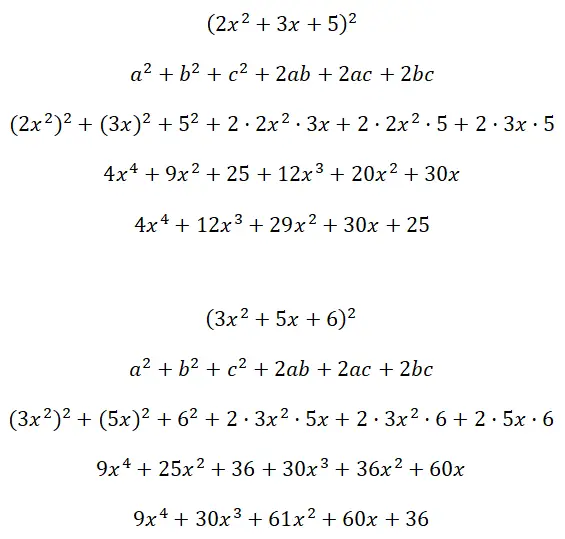ما هي المنتجات الرائعة أو الهويات الرائعة؟
المتطابقات الرائعة ، والتي تسمى أيضًا المنتجات الرائعة أو المساواة الرائعة ، هي موارد رياضية تسمح بحل منتجات وحواصل كثيرات الحدود بسرعة أكبر. وكما تشير كلمة الهوية، فهذه هي المعادلات التي تتيح لنا حساب هذه العمليات دون الحاجة إلى حلها. وبما أننا نعلم أن هذا التعبير يتبع قواعد ثابتة (يتم استيفاؤها دائمًا)، وبالتالي يمكننا الحصول على النتيجة دون الحاجة إلى التحقق منها.
متى تستخدم هوية بارزة؟
تُستخدم هذه المتطابقات بشكل أساسي في مجال الجبر، وتتمثل وظيفتها الرئيسية في تسريع حل معادلة متعددة الحدود، دون الحاجة إلى حل العملية بأكملها نفسها. ومن هنا نحصل على تركيبات المنتجات البارزة والتي سنعلق عليها طوال المقال. وأخيرًا، يمكننا تطبيق الصيغ على المربعات الكاملة، أو تحليل متعددات الحدود ، أو أي نوع آخر من العمليات الحسابية.
كيفية حل منتج رائع خطوة بخطوة؟
من أجل حل الهويات البارزة، تحتاج إلى اتباع إجراء بسيط جدًا، وهو أيضًا منطقي جدًا:
- تحديد نوع الهوية البارزة: الخطوة الأولى هي تحديد نوع العملية: منتج بارز أو حاصل ملحوظ. يجب عليك أيضًا توضيح نوع الصيغة التي ستحتاج إلى تطبيقها، على الرغم من أنك ستفهم ذلك لاحقًا، بمجرد أن نوضح الأنواع المختلفة للهويات البارزة.
- تطبيق الصيغة: بمجرد معرفة الصيغة التي تحتاج إلى تطبيقها، فقد حان الوقت لإجراء الحسابات. اعتمادًا على نوع الهوية، سيتعين عليك حل عمليات أكثر أو أقل تعقيدًا، وفي الغالبية العظمى من الحالات، ستتكون هذه الحسابات من مصطلحات تحتوي على مجهول واحد على الأقل.
- تبسيط التعبير: أخيرًا، عندما تحصل على النتيجة، عليك تبسيطها. في هذه الخطوة، تحتاج إلى تجميع المصطلحات المتشابهة وترتيبها لتكوين كثيرة الحدود الناتجة جيدة التنظيم. تجدر الإشارة إلى أن هذه الخطوة لا تقل أهمية عن الخطوات الأخرى، وإلا فإن التمرين يظل غير مكتمل.
صيغ الهويات البارزة أو المنتجات البارزة الرئيسية
ستجد أدناه جميع الصيغ المقابلة للهويات البارزة. بالإضافة إلى الشرح النظري لكل حالة، هناك أيضًا بعض الأمثلة البارزة على المنتجات التي تم حلها، والتي من خلالها ستفهم جميع المفاهيم بشكل أفضل. ومن الجدير بالذكر أنه في هذا القسم الأول ستجد فقط أهم الهويات . ولكن من خلال قراءة هذه المقالة، سوف تتعلم كيفية تطوير منتجات بارزة أكثر تعقيدًا، مثل تلك المصنوعة من ثلاثيات الحدود.
مربع من المبلغ
الحالة الأولى تتعلق بمربع المجموع ، وهو تعبير متعدد الحدود شائع جدًا في عالم الجبر. يمكن العثور على ذلك مكتوبًا بالشكل: (a + b) 2 وهو ما يعادل: (a + b) · (a + b). ومن ثم، فإننا نعلم أنه يمكن حلها باستخدام ضرب كثيرات الحدود. ولكن بفضل الهويات البارزة، يمكننا توفير الوقت باستخدام الصيغة التالية: (a + b) 2 = a 2 + 2ab + b 2 . بعد ذلك، نعرض لك عرضًا توضيحيًا للصيغة التي رأيناها للتو، وبهذه الطريقة ستتمكن من فهم مصدرها وكيفية استخدامها:
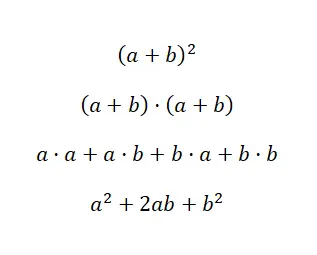
كما نرى، قمنا بالتحقق باستخدام ضرب كثيرات الحدود التي علقنا عليها سابقًا. ويمكننا أن نقول بكل تأكيد أنه إذا كنت تعرف الصيغة الناتجة عن ظهر قلب، فمن خلال إجراء استبدال بسيط للقيم ، يمكنك الحصول على النتيجة بشكل أسرع. لذلك فهو مفهوم رياضي مفيد للغاية. الآن بعد أن عرفت كيفية عمل مربع المجموع، سنعرض لك مثالًا ملموسًا:
مثال على مربع المبلغ
احسب الهوية البارزة (2x + 4) 2 :
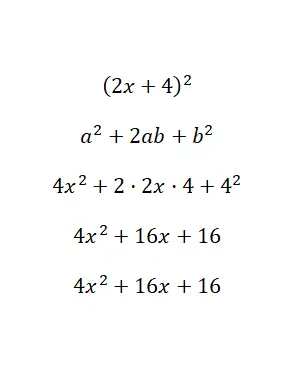
في الأساس، قمنا بربط قيم ذات الحدين بأحرف الصيغة وقمنا بحلها: a = 2x و b = 4. وأخيرا، بعد حل جميع العمليات الحسابية، حصلنا على كثيرة الحدود 4x 2 + 16x + 16، وهي يعادل الأصلي . في هذا المثال، حصلنا على كثيرة حدود موسعة (في الصورة القياسية) من كثيرة حدود مخفضة.
مربع الطرح
تعبير آخر شائع جدًا هو مربع الطرح ، والذي يشبه إلى حد كبير مربع الجمع، فهو يتغير بعلامة واحدة فقط. إذن فإن بنية ذات الحدين تعادل: (a – b) 2 ، وإذا فتحناها نحصل على: (a – b) · (a – b). كما في الحالة السابقة، يمكن حساب ذلك من ضرب كثيرات الحدود، على الرغم من أنه يحتوي أيضًا على صيغة تسهل الحل: a 2 – 2ab +b 2 . أدناه يمكنك العثور على الدليل التجريبي على ذلك:
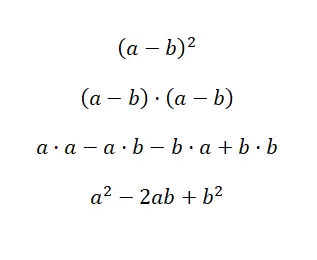
لتبسيط حل مربع الفرق، يمكننا استخدام نفس الصيغة التي استخدمناها لمجموع المربع، ولكن مع الإشارة الأولى سالبة . يسمح هذا التغيير البسيط بتكييف التعبير مع ذوات الحدين المكونة من حد موجب ومصطلح سالب، وهو أمر مفيد لعمليات الطرح. سنعرض لك الآن مثالاً تم حله:
مثال على مربع الطرح
احسب الهوية البارزة (x – 3) 2 :
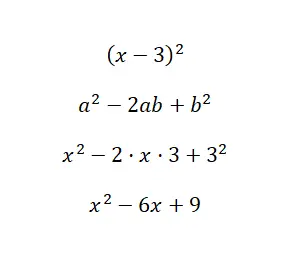
كما ترون في حل المثال، قمنا باستبدال قيم ذات الحدين في الصيغة، a = x وb = 3. لذلك، باستخدام الصيغة التي شرحناها سابقًا، كل ما علينا فعله هو الاستبدال وبعض الأمور الأساسية جدًا العمليات الحسابية. يتيح لنا هذا معرفة مدى سهولة حساب مربع الفرق باستخدام هذا التعبير.
فرق المربعات أو الجمع بالفرق
الحالة الثالثة من المنتجات البارزة تسمى فرق المربعات ، والتي تتكون من حاصل ضرب ذات الحدين الموجب وذو الحدين السالبين. تعبير هذا النمط له البنية التالية: (a + b) · (a – b)، لذلك إذا قمنا بتوسيع هذا المنتج نحصل على الصيغة التي تجعل الحساب أسهل: a 2 – b 2 . كما ترون، إنها صيغة بسيطة للغاية، على الرغم من أنه لفهمها بالكامل، يجب عليك تطوير جميع الحسابات:
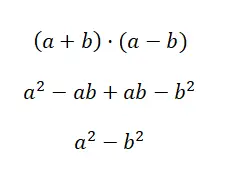
مثال على الجمع بالفرق
احسب الهوية البارزة (x + 1) · (x – 4):
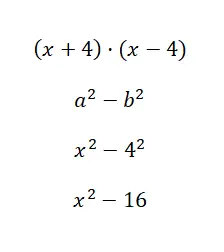
في هذه المناسبة، الحساب الرقمي سهل للغاية، في الواقع لم يكن علينا سوى حل قوة ما. على الرغم من أنه من الصحيح أن هذه الصيغة لا تنطبق إلا عندما يكون للثنائيات نفس الحد الرئيسي ونفس الحد المستقل، ولكن مع تغيير الإشارة. لذا فإن هذه الهوية مهمة، ولكنها ليست الهوية التي ستستخدمها أكثر من غيرها.
نتاج اثنين من الحدين مع مصطلح مشترك
وفي هذه الحالة الرابعة نجد أنفسنا أمام وضع مشابه جدًا للوضع السابق، مع وجود تعديل طفيف في البنية. لاحظ الفرق الذي نوضحه لك: (x + a) · (x + b) و (a + b) · (a – b). إذا كنت لا تزال لا ترى الأمر بشكل واضح، ففكر في المثال التالي: (x + 4) · (x + 5) و (x + 4) · (x – 4). في الحالة الأولى ( حاصل ضرب حدين مشتركين ) يوجد حد مشترك واحد فقط، بينما في الحالة الثانية (المجموع بالفرق) يكون الحدان مشتركين، لكن الحد المستقل له إشارته المعكوسة. ومع ذلك، دعونا نرى ما هي الصيغة التي يمكننا التصرف بها:
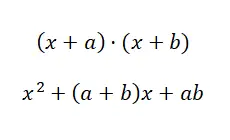
مثال على منتج ذو الحدين بمصطلح مشترك
أوجد المنتج البارز (x + 2) · (x + 3):
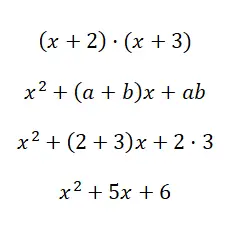
باستخدام صيغة x 2 + (a + b)x + ab يمكننا حساب كثيرة الحدود من الدرجة الثانية الناتجة عن ضرب الحدين. نأمل أن تكون قد فهمت من خلال هذا المثال الفرق بين الحالتين الأخيرتين اللتين شرحناهما، لأنه في بعض الأحيان قد يكون من الصعب التمييز بينهما.
مربع من ثلاثي الحدود
عندما نحاول حساب مربع ثلاثية الحدود، يكون لدينا أيضًا منتج رائع يجعل حياتنا أسهل. يتم تمثيل هذا التعبير على النحو التالي: (a + b + c) 2 والحاصل المكافئ هو: a 2 + b 2 + c 2 + 2ab + 2ac + 2bc. تجدر الإشارة إلى أن هذا صحيح في حالة ثلاثية الحدود الموجبة، ولكن إذا كان أحد المعاملات سالبًا، فأنت بحاجة فقط إلى كتابة القيمة السالبة في الصيغة. فيما يلي عرض للصيغة:
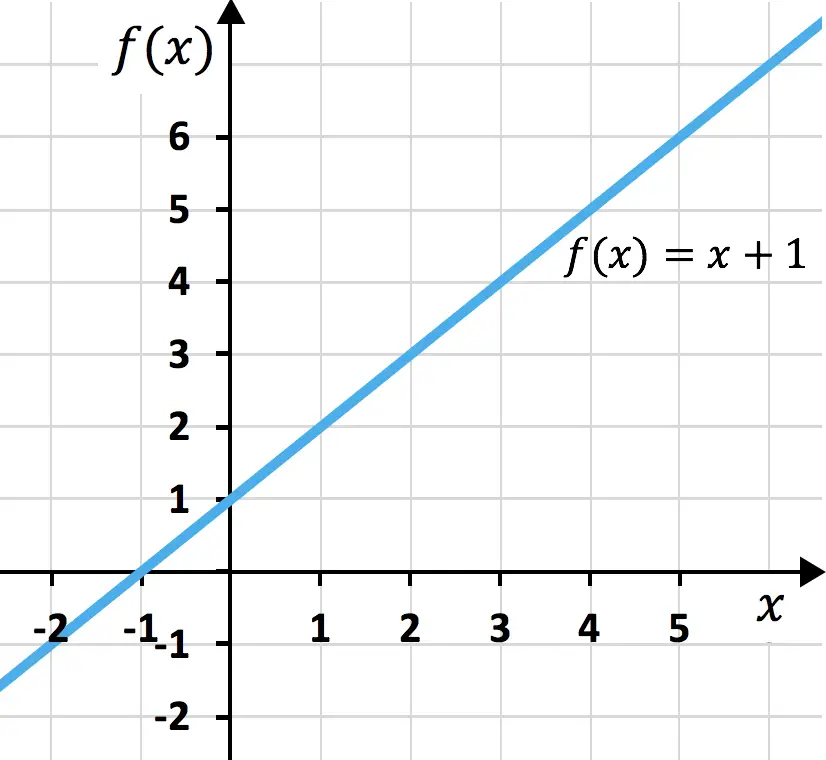
مثال على مربع ثلاثي الحدود
احسب الهوية البارزة (2x + 1 + x 2 ) 2 :
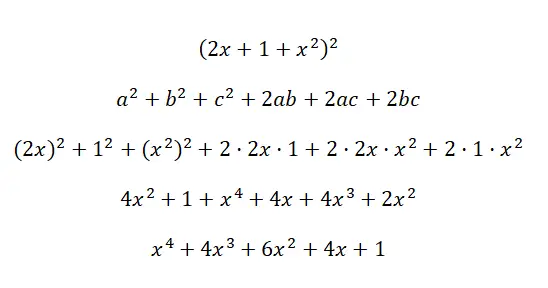
صيغ هوية رائعة أو منتجات مكعبة رائعة
الآن بعد أن شرحنا المتطابقات الرئيسية البارزة، سننظر إلى مشتقاتها ، بدءًا من ذات الحدين المكعبة. لحساب المنتجات البارزة من هذا النمط، سيتعين علينا اللجوء إلى صيغ أكثر تعقيدًا بعض الشيء، ولكنها تتبع بنية مشابهة لتلك التي ناقشناها بالفعل.
مكعب ذو الحدين
يكتب مكعب ذات الحدين : (a + b) 3 و (a – b) 3 ، وهذا التعبير يكافئ الصيغة التالية: (a 3 + 3a 2 b + 3ab 2 + b 3 )، و (a 3) – 3 أ 2 ب + 3 ب 2 – ب 3 ). وتسمى هاتان الحالتان مكعب المجموع ومكعب الطرح، لأنهما ذوات حدين مكعبة. ستجد أدناه عرضًا تفصيليًا للغاية لكل حالة:
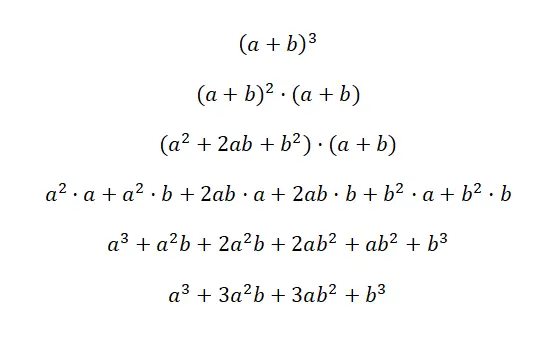
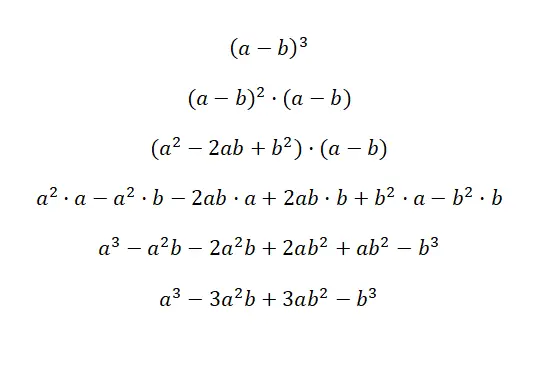
المفتاح لفهم هذا الدليل الأول هو أن نفهم أن (أ + ب) 3 يعادل: (أ + ب) 2 · (أ + ب). وبهذه الطريقة نستخدم صيغة مربع المجموع التي شرحناها سابقًا لضرب العامل الآخر. ثم نقوم ببساطة بتبسيط التعبير، ونحصل على المتطابقة البارزة المقابلة: a 3 + 3a 2 b + 3ab 2 + b 3 . وفي حالة المثال الثاني، يحدث نفس الشيء، ولكن مع تغيير الإشارة.
مثال على مكعب ذو الحدين
حل الهوية البارزة (x + 3) 3 :
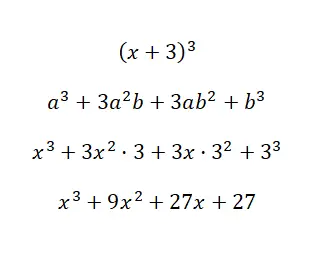
باستخدام الصيغة التي ناقشناها للتو، يمكننا حساب كثيرة الحدود، مع الأخذ في الاعتبار أن: a = xyb = 3. كما ترون، الإجراء بسيط للغاية ولا يحتوي على الكثير من التعقيدات في الحساب، وذلك لأننا لدينا الصيغة . وإلا فإن الاضطرار إلى القيام بهذا القدر من الضرب سيكون أمرًا مملاً للغاية.
مجموع المكعبات والفرق بين المكعبات
لدينا أيضًا هذه الحالة الأخرى، والتي يمكن الخلط بينها بسهولة مع الحالة السابقة. على الرغم من أن الحالتين مكتوبتان بشكل مختلف، إلا أنهما غير متكافئتين. التعبير المعادل لمجموع المكعبات أو الفرق بينها هو: a 3 + b 3 بينما تحدثنا في الحالة السابقة عن: (a + b) 3 . كما ترون، هناك تشابه لا يمكن إنكاره في بنية التعبير، ولكن في الواقع، عندما يتعلق الأمر بتطوير الحساب، فإنهما حالتان مختلفتان تمامًا:
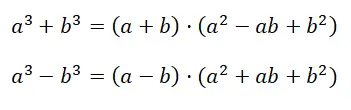
في عرض الصيغة، نحصل على تحليل كثيرة الحدود الأولى ، وبالتحديد ننتقل من ذات الحدين الأولي إلى حاصل ضرب ذات الحدين في ثلاثي الحدود. يبدو أن النتيجة التي تم الحصول عليها (a + b) · (a 2 – ab + b 2 )، لا تبسط العملية الحسابية على الإطلاق، ولكن في الواقع، من خلال تحليل كثير الحدود نحصل على تعبير يسهل فهمه.
مثال على مجموع المكعبات
احسب المنتج البارز × 3 + 27:
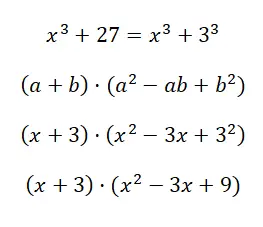
في هذه الحالة، النتيجة التي نحصل عليها طويلة جدًا، لأنه لا يمكن تبسيطها أكثر. لكن، من الطبيعي التوصل إلى هذا التعبير، في الواقع، في هذه الحالات، لا يمكنك الحصول إلا على نتيجة ذات بنية مكافئة لمنتج ذات الحدين في ثلاثي الحدود، كما في هذا المثال.
ثلاثي مكعب
يُكتب مكعب ثلاثية الحدود : (a + b + c) 3 ، وهو ما يعني ضرب ثلاثة ثلاثية حدود متطابقة، لكن بدون أس: (a + b + c) · (a + b + c) · (a + b) + ج). إنه المنتج الأكثر تعقيدًا على الإطلاق، على الرغم من أن الصيغة منطقية تمامًا ويتم الحصول عليها بنفس الطريقة مثل الجميع، عند إجراء الضرب المقابل لكثيرات الحدود. ستجد أدناه دليلاً على صيغة هذه الهوية الرائعة:
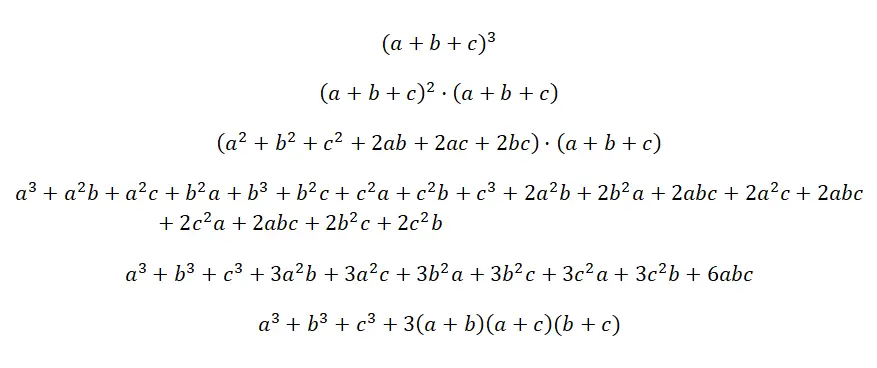
مثال على مكعب ثلاثي الحدود
حل المكعب الثلاثي الحدود التالي (x 2 + 3x – 4) 3 :
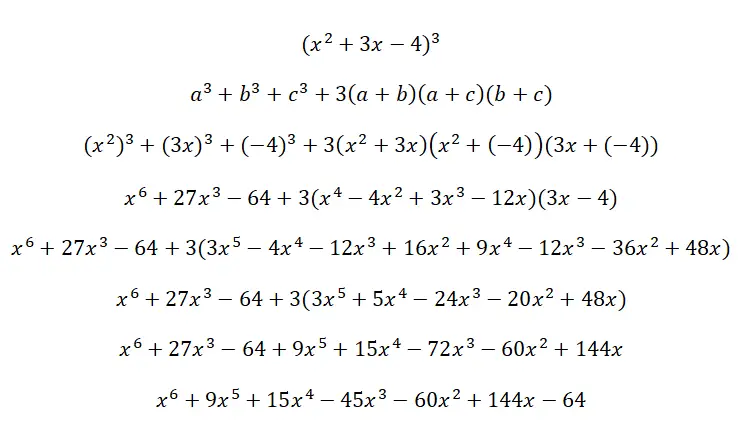
نسب ملحوظة
أخيرًا، سنشرح النواتج البارزة ، وهي هويات بارزة لحل أنواع معينة من الكسور الجبرية بسرعة. بتعبير أدق، هناك أربعة أنواع مختلفة، تشترك في خاصية واحدة: نتائجها تتكون من كثيرات الحدود الدقيقة (مع الباقي يساوي الصفر). ومن الجدير بالذكر أيضًا أن صيغ النواتج المميزة لها علاقة معينة بصيغ النواتج الرائعة التي شرحناها سابقًا.
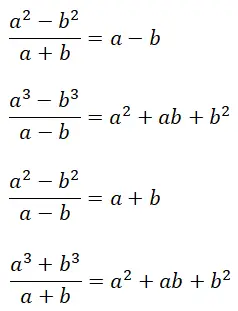
مثال على النسب الرائعة التي تم حلها
احسب النسب الملحوظة التالية:
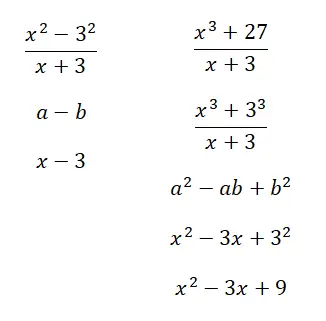
تم حل تمارين المنتج الرائعة
الآن بعد أن عرفت كيف يتم حل الشخصيات البارزة المختلفة، فقد حان الوقت لكي تتدرب قليلاً. ولهذا السبب نقدم لك 6 تمارين لتطبيق كل النظرية الموضحة. ونعرض لك جدولاً بأهم المتطابقات البارزة، بحيث يكون في متناول يدك أثناء حل جميع التمارين:

التمرين 1
حل المربعات ذات الحدين (x – 4) 2 , (x + 1) 2 و (x – 3) 2 :
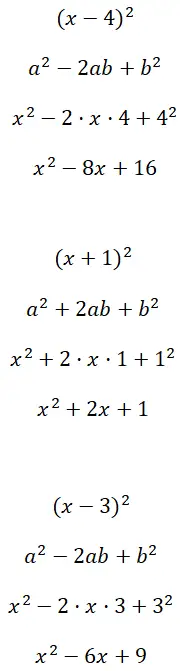
تمرين 2
احسب الفرق بين المربعين (x – 1) · (x + 1) و (x + 3) · (x – 3):
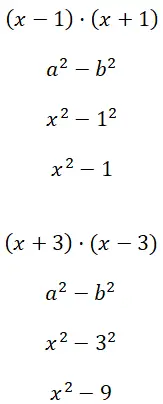
التمرين 3
تطوير النواتج البارزة للمكعب (س – 5) 3 و (س + 8) 3 :
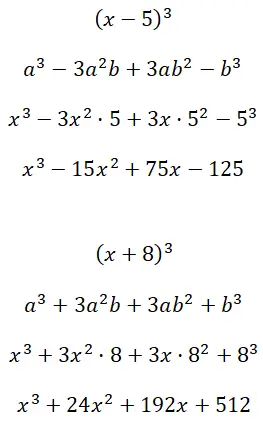
التمرين 4
طوّر هويات بارزة مكونة من مصطلحات متعددة العوامل (4x 2 + 5y) 2 , (5x 3 + y 2 ) · (5x 3 – y 2 ) و (5x 2 – 2xy) 2 :
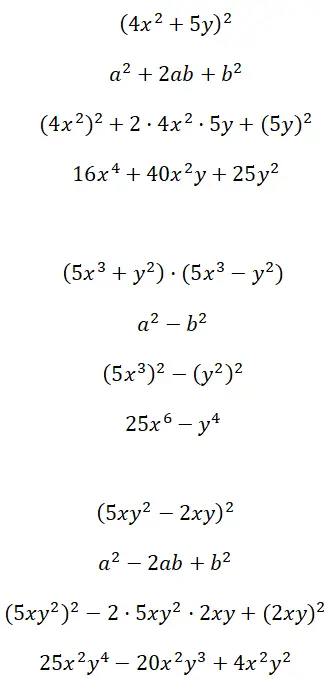
التمرين 5
احسب النواتج المكعبة البارزة التي تكونها الحدود متعددة العوامل (3x 2 + y) 3 و (5y 3 – 2x 2 ) 3 :
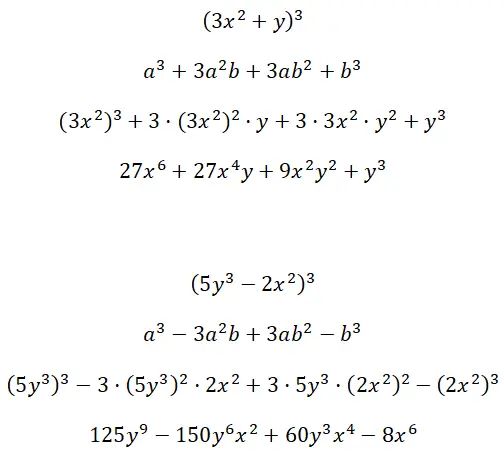
التمرين 6
حل مربعات ثلاثية الحدود (2x 2 + 3x + 5) 2 و (3x 2 + 5x + 6):