مناقشة أنظمة المعادلات مع المعلمات -

في هذه الصفحة سوف نرى كيفية مناقشة وحل نظام المعادلات مع المعلمات . بالإضافة إلى ذلك، ستجد أمثلة وتمارين محلولة لأنظمة المعادلات الخطية للتدرب عليها.

من ناحية أخرى، لتحليل أنظمة المعادلات الخطية، من المهم أن تعرف ما هي قاعدة كرامر وما هي نظرية روشيه-فروبينيوس ، لأننا سنستخدمهما باستمرار.

مثال لنظام المعادلات الخطية مع المعلمات

ناقش وحل نظام المعادلات التالي بدلالة المعلمة m :

$\begin{cases} x+y+2z= 2 \\[1.5ex] -x+my+2z=0 \\[1.5ex] 3x+mz = 4\end{cases}$

نقوم أولاً بإنشاء المصفوفة A والمصفوفة الموسعة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & m & 2 & 0 \\[1.1ex] 3 & 0 & m & 4 \end{array} \right)$

الآن نحل محدد A باستخدام قاعدة ساروس لمعرفة رتبة المصفوفة:

$\displaystyle\begin{aligned} \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} & =m^2+6+0-6m-0+m \\ & = m^2-5m+6 \end{aligned}$

لذا فإن نتيجة محدد A تعتمد على قيمة m . لذلك سنرى أي قيم m سيختفي المحدد. للقيام بذلك، قمنا بتعيين النتيجة تساوي 0 :

$\displaystyle m^2-5m+6 = 0$

ونحل المعادلة التربيعية بالصيغة:

$\displaystyle m = \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle m = \cfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 1 \cdot 6}}{2 \cdot 1} = \cfrac{5 \pm \sqrt{25-24}}{2} =\cfrac{5 \pm 1}{2} = \begin{cases} \bm{m = 3} \\[2ex] \bm{m =2} \end{cases}$

لذلك عندما يكون m يساوي 2 أو 3، فإن محدد A سيكون 0. وعندما يكون m مختلفًا عن 2 ومختلفًا عن 3، فإن محدد A سيكون مختلفًا عن 0.

ولذلك يجب علينا تحليل كل حالة على حدة:

م ≠ 3 و م ≠ 2:

كما رأينا للتو، عندما تكون المعلمة m مختلفة عن 2 و 3، فإن محدد المصفوفة A يختلف عن 0. وبالتالي، فإن رتبة A هي 3 .

$\displaystyle rg(A)=3$

علاوة على ذلك، فإن رتبة المصفوفة A’ هي أيضًا 3 ، لأن بداخلها مصفوفة فرعية 3×3 يختلف محددها عن 0. ولا يمكن أن تكون من الرتبة 4 لأننا لا نستطيع إنشاء محدد 4×4.

$\displaystyle rg(A')=3$

ثم، بما أن رتبة المصفوفة A تساوي رتبة المصفوفة A’ وعدد المجهولات في النظام (3)، فمن خلال نظرية Rouché-Frobenius نعلم أنه نظام محدد متوافق (SCD). :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

بمجرد أن نعرف أن النظام هو نظام محدد متوافق (DCS)، فإننا نطبق قاعدة كرامر لحله. للقيام بذلك، تذكر أن المصفوفة A ومحددتها والمصفوفة A’ هي:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} = m^2-5m+6$

لحساب x باستخدام قاعدة كرامر، نقوم بتغيير العمود الأول من محدد المصفوفة A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle\bm{x} = \cfrac{\begin{vmatrix} 2 & 1 & 2\\[1.1ex]0&m&2 \\[1.1ex] 4 & 0 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{2m^2+8-8m}{m^2-5m+6}$

لحساب y باستخدام قاعدة كرامر، نقوم بتغيير العمود الثاني من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 0 & 2 \\[1.1ex] 3 & 4 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-4+2m}{m^2-5m+6}$

لحساب z باستخدام قاعدة كرامر، نقوم بتغيير العمود الثالث من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-2m+4}{m^2-5m+6}$

ولذلك فإن حل نظام المعادلات للحالة m≠3 وm≠2 هو:

$\displaystyle \bm{x =} \cfrac{\bm{2m^2+8-8m}}{\bm{m^2-5m+6}} \qquad \bm{y=} \cfrac{\bm{-4+2m}}{\bm{m^2-5m+6}} \qquad \bm{z =} \cfrac{\bm{-2m+4}}{\bm{m^2-5m+6}}$

كما ترون، في هذه الحالة حل نظام المعادلات هو دالة لـ m.

بمجرد إيجاد الحل عندما يكون m مختلفًا عن 2 و 3، سنحل النظام عندما يكون m يساوي 2:

م=2:

سنقوم الآن بتحليل النظام عندما تكون المعلمة m مساوية لـ 2. في هذه الحالة المصفوفات A و A’ هي:

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 2 & 2 \\[1.1ex] 3 & 0 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 2 & 2 & 0 \\[1.1ex] 3 & 0 & 2 & 4 \end{array} \right)$

كما رأينا سابقاً، عندما m=2 فإن محدد A هو 0. وبالتالي فإن المصفوفة A ليست من الرتبة 3. لكن بداخلها محددات 2×2 تختلف عن 0، على سبيل المثال:

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0$

إذن، في هذه الحالة ، رتبة A هي 2 :

$\displaystyle rg(A)=2$

بمجرد أن نعرف رتبة المصفوفة A، نحسب رتبة A’. محدد الأعمدة الثلاثة الأولى يعطي 0، لذلك جربنا المحددات الأخرى 3×3 في المصفوفة A’:

$\displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 0 & 2 & 4 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 2 & 4 \end{vmatrix}=0\qquad \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}=0$

جميع المحددات الممكنة للبعد 3×3 تعطي 0. لكن من الواضح أن المصفوفة A’ لها نفس المحدد 2×2 غير 0 مثل المصفوفة A:

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0$

وبالتالي فإن المصفوفة A’ هي أيضًا من المرتبة 2 :

$\displaystyle rg(A')=2$

لذا، بما أن رتبة المصفوفة A تساوي رتبة المصفوفة A’ لكن هاتين الرتبتين أصغر من عدد المجهولات في النظام (3)، فإننا نعرف من خلال نظرية روشيه-فروبينيوس أنه نظام متوافق بشكل غير محدد (المركز الدولي):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

وبما أنه ICS، نحن بحاجة إلى تحويل النظام لحلها. للقيام بذلك، يجب علينا أولا حذف معادلة من النظام، في هذه الحالة سوف نقوم بحذف المعادلة الأخيرة:

$\begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \\[1.5ex] \cancel{3x+2z = 4} \end{cases} \longrightarrow \quad \begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0\end{cases}$

الآن دعونا نحول المتغير z إلى lect:

$\begin{cases}x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+y+2\lambda= 2 \\[1.5ex] -x+2y+2\lambda=0\end{cases}$

ونضع الحدود مع α مع الحدود المستقلة:

$\begin{cases}x+y=2-2\lambda \\[1.5ex] -x+2y=-2\lambda \end{cases}$

لذلك، تظل المصفوفة A والمصفوفة A’ للنظام كما يلي:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 1 \\[1.1ex] -1 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 1 & 2 -2\lambda \\[1.1ex] -1 & 2 & -2\lambda \end{array} \right)$

أخيرًا، بمجرد أن نقوم بتحويل النظام، فإننا نطبق قاعدة كرامر . للقيام بذلك، نقوم أولاً بحل محدد A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 \\[1.1ex] -1 & 2\end{vmatrix} =2-(-1)=3$

لحساب x باستخدام قاعدة كرامر، نقوم بتغيير العمود الأول من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 -2\lambda & 1 \\[1.1ex] -2\lambda & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{4-4\lambda-(-2\lambda)}{3} = \cfrac{\bm{4-2\lambda}}{\bm{3}}$

لحساب y باستخدام قاعدة كرامر، نقوم بتغيير العمود الثاني من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 2 -2\lambda \\[1.1ex] -1 & -2\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-2\lambda -(-2+2\lambda)}{3} = \cfrac{\bm{2-4\lambda} }{\bm{3}}$

بحيث عندما تكون m=2 يكون حل نظام المعادلات دالة لـ lect، لأنه من SCI وبالتالي له حلول لا نهائية:

$\displaystyle \bm{x =} \cfrac{\bm{4-2\lambda}}{\bm{3}} \qquad \bm{y=}\cfrac{\bm{2-4\lambda}}{\bm{3}} \qquad \bm{z=\lambda}$

لقد قمنا بالفعل بتحليل حل النظام عندما تكون المعلمة m مختلفة عن 2 و 3، وعندما تساوي 2. لذلك نحتاج فقط إلى الحالة الأخيرة: عندما تأخذ m القيمة 3:

م=3:

سنقوم الآن بتحليل ما يحدث عندما تكون المعلمة m تساوي 3. في هذه الحالة المصفوفات A و A’ هي:

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 3 & 2 \\[1.1ex] 3 & 0 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 3 & 2 & 0 \\[1.1ex] 3 & 0 & 3 & 4 \end{array} \right)$

كما رأينا سابقًا، عندما m=3 فإن محدد A هو 0. وبالتالي فإن المصفوفة A ليست من الرتبة 3. لكن بداخلها محددات 2×2 تختلف عن 0، على سبيل المثال:

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 3 \end{vmatrix} = 3 - (-1)=4 \neq 0$

إذن، في هذه الحالة ، رتبة A هي 2 :

$\displaystyle rg(A)=2$

بمجرد أن نعرف رتبة المصفوفة A، نحسب رتبة A’. محدد الأعمدة الثلاثة الأولى يعطي 0، لذلك نحاول استخدام محدد 3×3 آخر داخل المصفوفة A’، على سبيل المثال محدد الأعمدة الثلاثة الأخيرة:

$\displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 3 & 2 & 0 \\[1.1ex] 0 & 3 & 4\end{vmatrix}=2$

من ناحية أخرى، تحتوي المصفوفة A’ على محدد نتيجته مختلفة عن 0، وبالتالي فإن المصفوفة A’ تأتي في المرتبة 3 :

$\displaystyle rg(A')=3$

وبالتالي، عندما تكون m = 3، تكون رتبة المصفوفة A أقل من رتبة المصفوفة A’. وهكذا، من نظرية روشيه-فروبينيوس، نستنتج أن النظام هو نظام غير متوافق (IS) :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas}=3\end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A)=2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

ولذلك، فإن نظام المعادلات ليس له حل عندما يكون m = 3.

ملخص المثال:

كما رأينا فإن حل نظام المعادلات يعتمد على قيمة المعلمة m . فيما يلي ملخص لجميع الحالات المحتملة:

م ≠ 3 و م ≠ 2:

$\displaystyle \bm{SCD} \longrightarrow \begin{cases} x = \cfrac{2m^2+8-8m}{m^2-5m+6} \\[3.5ex] y =\cfrac{-4+2m}{m^2-5m+6} \\[3.5ex] z = \cfrac{-2m+4}{m^2-5m+6} \end{cases}$

م=2:

$\displaystyle \bm{SCI} \longrightarrow \begin{cases} x = \cfrac{4-2\lambda}{3} \\[3.5ex] y= \cfrac{2-4\lambda}{3} \\[3.5ex] z = \lambda \end{cases}$

م=3:

$\displaystyle \bm{SI} \longrightarrow$

النظام ليس لديه حل.

هنا قمنا بالعملية برمتها باستخدام نظرية روش وقاعدة كرامر، ولكن يمكن أيضًا مناقشة أنظمة المعادلات ذات المعلمات وحلها باستخدام طريقة غاوس (مع التمارين) . يمكنك التعرف على المزيد حول هذه الطريقة في الصفحة المرتبطة، حيث ستجد شرحًا تفصيليًا للإجراء بالإضافة إلى أمثلة وتمارين محلولة خطوة بخطوة.

حل مسائل المناقشة لأنظمة المعادلات الخطية ذات المعلمات

التمرين 1

ناقش وحل النظام التالي من المعادلات الخطية المعتمدة على المعلمات:

انظر الحل

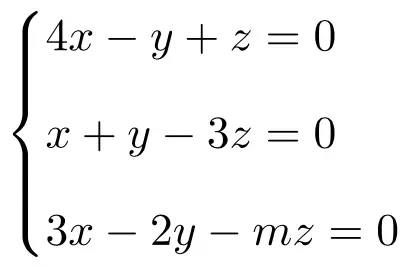
نقوم أولاً بإنشاء المصفوفة A والمصفوفة الموسعة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)$

يجب علينا الآن العثور على رتبة المصفوفة A. للقيام بذلك، نتحقق مما إذا كان محدد المصفوفة بأكملها مختلفًا عن 0:

$\displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{vmatrix} & =-4m+9-2-3-24-m \\ & =-5m-20 \end{aligned}$

تعتمد نتيجة محدد A على قيمة m. لذلك سنرى أي قيم m سيختفي المحدد. للقيام بذلك، نساوي النتيجة الناتجة بـ 0 ونحل المعادلة:

$-5m-20 = 0$

$-5m = 20$

$m = \cfrac{20}{-5} = -4$

لذلك، عندما تكون m -4، فإن محدد A سيكون 0. وعندما يكون m مختلفًا عن -4، سيكون محدد A مختلفًا عن 0. لذلك يجب علينا تحليل كل حالة على حدة:

م≠-4:

كما رأينا للتو، عندما تختلف المعلمة m عن -4، فإن محدد المصفوفة A يختلف عن 0. وبالتالي، فإن رتبة A هي 3.

$\displaystyle rg(A)=3$

علاوة على ذلك، فإن رتبة المصفوفة A’ هي أيضًا 3، لأن بداخلها مصفوفة فرعية 3×3 يختلف محددها عن 0. ولا يمكن أن تكون في المرتبة 4 لأننا لا نستطيع تكوين محدد 4×4.

$\displaystyle rg(A')=3$

لذلك، من خلال تطبيق نظرية روشيه-فروبينيوس، نعلم أن هذا نظام محدد متوافق (SCD)، لأن مدى A يساوي نطاق A’ وعدد المجهولين.

بمجرد أن نعرف أن النظام هو SCD، نطبق قاعدة كرامر لحلها. للقيام بذلك، تذكر أن المصفوفة A ومحددتها والمصفوفة A’ هي:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)$

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m\end{vmatrix} =-5m-20$

لحساب xatex] باستخدام قاعدة كرامر، نقوم بتغيير العمود الأول من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 0 & -1 & 1 \\[1.1ex] 0 & 1 & -3 \\[1.1ex] 0 & -2 & -m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

لحساب المجهول وبقاعدة كرامر نقوم بتغيير العمود الثاني من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & 0 & 1 \\[1.1ex] 1 & 0 & -3 \\[1.1ex] 3 & 0 & -m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

لحساب z باستخدام قاعدة كرامر، نقوم بتغيير العمود الثالث من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

ولذلك فإن حل نظام المعادلات للحالة m≠-4 هو:

س=0 ص=0 ض=0

م=-4:

سنقوم الآن بتحليل النظام عندما تكون المعلمة m هي -4. في هذه الحالة المصفوفتان A و A’ هما:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & 4 & 0\end{array} \right)$

كما رأينا سابقًا، عندما m=-4 فإن محدد A هو 0. إذن، المصفوفة A ليست من الرتبة 3. لكن بداخلها محددات 2×2 مختلفة عن 0، على سبيل المثال:

$\displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0$

بما أن المصفوفة لها محدد من الرتبة 2 يختلف عن 0، فإن المصفوفة A من الرتبة 2:

$\displaystyle rg(A)=2$

بمجرد أن نعرف رتبة “أ”، فإننا نحسب رتبة “أ”. نحن نعلم بالفعل أن محدد الأعمدة الثلاثة الأولى يعطي 0، لذلك جربنا المحددات الأخرى الممكنة 3×3:

$\displaystyle \begin{vmatrix} -1 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] -2 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] 3 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0\end{vmatrix} = 0$

جميع المحددات 3×3 للمصفوفة A’ هي 0، وبالتالي فإن المصفوفة A’ لن تكون في المرتبة 3 أيضًا. ومع ذلك، بداخله محددات للترتيب 2 تختلف عن 0. على سبيل المثال:

$\displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0$

وبالتالي فإن المصفوفة A’ ستكون من المرتبة 2:

$\displaystyle rg(A')=2$

مدى المصفوفة A يساوي مدى المصفوفة A’ لكن هاتين المصفوفتين أصغر من عدد العناصر المجهولة في النظام (3)، وبالتالي، وفقًا لنظرية Rouché-Frobenius، c هو نظام متوافق غير محدد (ICS):

إنه نظام ICS، لذا نحتاج إلى تحويل النظام لحله. نقوم أولاً بحذف معادلة واحدة، والتي في هذه الحالة ستكون الأخيرة:

$\begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0 \\[1.5ex] \cancel{3x-2y+4z = 0} \end{cases} \longrightarrow \quad \begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0\end{cases}$

الآن دعونا نحول المتغير z إلى lect:

$\begin{cases}4x-y+z= 0 \\[1.5ex] x+y-3z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 4x-y+\lambda= 0 \\[1.5ex] x+y-3\lambda=0\end{cases}$

ونضع الحدود مع α مع الحدود المستقلة:

$\begin{cases} 4x-y=-\lambda \\[1.5ex] x+y=3\lambda \end{cases}$

بحيث تبقى المصفوفة A والمصفوفة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 \\[1.1ex] 1 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 4 & -1 & -\lambda \\[1.1ex] 1 & 1 & 3\lambda \end{array} \right)$

وأخيرا، بمجرد أن نحول النظام، فإننا نطبق قاعدة كرامر. للقيام بذلك، نقوم أولاً بحل محدد A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} = 4-(-1)=5$

لحساب x باستخدام قاعدة كرامر، نقوم بتغيير العمود الأول من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix}-\lambda & -1 \\[1.1ex] 3\lambda & 1 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-\lambda-(-3\lambda)}{5} =\cfrac{\bm{2\lambda}}{\bm{5}}$

لحساب المجهول وبقاعدة كرامر نقوم بتغيير العمود الثاني من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & -\lambda \\[1.1ex] 1 & 3\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12\lambda-(-\lambda)}{5}=\cfrac{\bm{13\lambda}}{\bm{5}}$

بحيث عندما تكون m=-4 يكون حل نظام المعادلات دالة لـ lect، لأنه من SCI وبالتالي له حلول لا نهائية:

$\displaystyle \bm{x =}\cfrac{\bm{2\lambda}}{\bm{5}}\qquad \bm{y=}\cfrac{\bm{13\lambda}}{\bm{5}} \qquad \bm{z=\lambda}$

تمرين 2

ناقش وأوجد الحل لنظام المعادلات الخطية المعتمدة على المعلمات التالي:

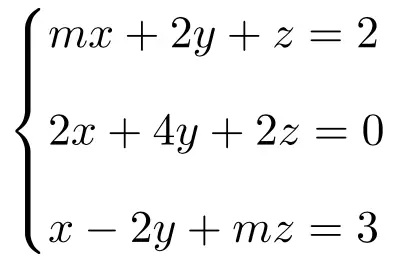
تمرين حل نظام المعادلات الخطية خطوة بخطوة مع المعلمات

انظر الحل

أول ما يجب فعله هو المصفوفة A والمصفوفة الموسعة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc} m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}m & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & m & 3\end{array} \right)$

يجب علينا الآن العثور على رتبة المصفوفة A. للقيام بذلك، نتحقق مما إذا كان محدد المصفوفة بأكملها مختلفًا عن 0:

$\displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix} & =4m^2+4-4-4+4m-4m \\ & =4m^2-4 \end{aligned}$

$4m^2-4 = 0$

$4m^2=4$

$m^2 = \cfrac{4}{4}$

$m^2 = 1$

$m = \pm 1$

لذلك، عندما يكون m +1 أو -1، فإن محدد A سيكون 0. وعندما يختلف m عن +1 و -1، فإن محدد A سيكون مختلفًا عن 0. لذلك يجب علينا تحليل كل حالة من خلال:

م≠+1 و م≠-1:

كما رأينا للتو، عندما تكون المعلمة m مختلفة عن +1 و -1، فإن محدد المصفوفة A يختلف عن 0. وبالتالي، فإن رتبة A هي 3.

$\displaystyle rg(A)=3$

$\displaystyle rg(A')=3$

بمجرد أن نعرف أن النظام هو SCD، نطبق قاعدة كرامر لحلها. للقيام بذلك، تذكر أن المصفوفة A ومحددتها والمصفوفة A’ هي:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix}=4m^2-4$

لحساب x باستخدام قاعدة كرامر، نقوم بتغيير العمود الأول من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2& 2 & 1 \\[1.1ex] 0 & 4 & 2 \\[1.1ex] 3 & -2 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{8m+8}}{\bm{4m^2-4}}$

لحساب المجهول وبقاعدة كرامر نقوم بتغيير العمود الثاني من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} m & 2 & 1 \\[1.1ex] 2 & 0 & 2 \\[1.1ex] 1 & 3 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{-10m+10}}{\bm{4m^2-4}}$

لحساب z باستخدام قاعدة كرامر، نقوم بتغيير العمود الثالث من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix}m & 2 & 2 \\[1.1ex] 2 & 4 & 0 \\[1.1ex] 1 & -2 & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{12m-28}}{\bm{4m^2-4}}$

ولذلك فإن حل نظام المعادلات للحالة m≠+1 وm≠-1 هو:

$\displaystyle \bm{x = }\cfrac{\bm{8m+8}}{\bm{4m^2-4}} \qquad \bm{y=}\cfrac{\bm{-10m+10}}{\bm{4m^2-4}}\qquad \bm{z =} \cfrac{\bm{12m-28}}{\bm{4m^2-4}}$

م=+1:

سنقوم الآن بتحليل النظام عندما تكون المعلمة m مساوية لـ 1. في هذه الحالة تكون المصفوفات A و A’ هي:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & 1 & 3\end{array} \right)$

كما رأينا سابقًا، عندما m=+1 يكون محدد A هو 0. وبالتالي فإن المصفوفة A ليست من الرتبة 3. لكن بداخلها محددات 2×2 مختلفة عن 0، على سبيل المثال:

$\displaystyle \begin{vmatrix}2 & 4\\[1.1ex] 1 & -2 \end{vmatrix} =-4-4=-8 \neq 0$

بما أن المصفوفة لها محدد من الرتبة 2 يختلف عن 0، فإن المصفوفة A من الرتبة 2:

$\displaystyle rg(A)=2$

بمجرد أن نعرف رتبة “أ”، فإننا نحسب رتبة “أ”. نحن نعلم بالفعل أن محدد الأعمدة الثلاثة الأولى يعطي 0، لذلك نحاول الآن، على سبيل المثال، مع محدد الأعمدة الثلاثة الأخيرة:

$\displaystyle \begin{vmatrix} 2 & 1 & 2 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -2 & 1 & 3 \end{vmatrix} = 16$

من ناحية أخرى، تحتوي المصفوفة A’ على محدد 3×3 الذي تختلف نتيجته عن 0، بحيث تكون المصفوفة A’ في المرتبة 3:

$\displaystyle rg(A')=3$

وبالتالي، عندما تكون m=+1 تكون رتبة المصفوفة A أصغر من رتبة المصفوفة A’. وهكذا، من نظرية روشيه-فروبينيوس، نستنتج أن النظام هو نظام غير متوافق (IS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

ولذلك فإن نظام المعادلات ليس له حل عندما m=+1 لأنه نظام غير متوافق.

م=-1:

سنقوم الآن بتحليل النظام عندما تكون المعلمة m هي -1. في هذه الحالة المصفوفتان A و A’ هما:

$\displaystyle A= \left( \begin{array}{ccc} -1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}-1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & -1 & 3\end{array} \right)$

كما رأينا سابقًا، عندما m=-1 فإن محدد A هو 0. إذن، المصفوفة A ليست من الرتبة 3. لكن بداخلها محددات 2×2 مختلفة عن 0، على سبيل المثال:

$\displaystyle \begin{vmatrix}-1 & 2\\[1.1ex] 2 & 4 \end{vmatrix} =-4-4=-8 \neq 0$

بما أن المصفوفة لها محدد من الرتبة 2 يختلف عن 0، فإن المصفوفة A من الرتبة 2:

$\displaystyle rg(A)=2$

بمجرد أن نعرف رتبة “أ”، فإننا نحسب رتبة “أ”. نحن نعلم بالفعل أن محدد الأعمدة الثلاثة الأولى يعطي 0، لذلك نحاول الآن، على سبيل المثال، مع محدد الأعمدة 1 و3 و4:

$\displaystyle \begin{vmatrix} -1 & 1 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 1 & -1 & 3\end{vmatrix} = -20$

من ناحية أخرى، تحتوي المصفوفة A’ على محدد 3×3 الذي تختلف نتيجته عن 0، بحيث تكون المصفوفة A’ في المرتبة 3:

$\displaystyle rg(A')=3$

وبالتالي، عندما تكون m = -1، تكون رتبة المصفوفة A أقل من رتبة المصفوفة A’. وهكذا، من نظرية روشيه-فروبينيوس، نستنتج أن النظام هو نظام غير متوافق (IS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

ولذلك فإن نظام المعادلات ليس له حل عندما تكون m=-1 لأنه نظام غير متوافق.

مثال لنظام المعادلات الخطية مع المعلمات

ملخص المثال:

حل مسائل المناقشة لأنظمة المعادلات الخطية ذات المعلمات

التمرين 1

تمرين 2

اترك تعليقاً إلغاء الرد