سنرى في هذا القسم كيفية مناقشة وحل نظام من المعادلات بطريقة غاوس-جوردان . أي تحديد ما إذا كان نظامًا متوافقًا محددًا (DCS)، أو نظامًا متوافقًا غير محدد (ICS)، أو نظامًا غير متوافق. بالإضافة إلى ذلك، ستجد أمثلة وتمارين محلولة حتى تتمكن من ممارسة المفاهيم واستيعابها بشكل مثالي.
لكي نفهم ما سنشرحه بعد ذلك، من المهم أن تعرف بالفعل كيفية حل نظام باستخدام طريقة غاوس ، لذلك نوصي بإلقاء نظرة قبل المتابعة.
الأنظمة المتوافقة التي تحددها طريقة غاوس
طالما أن الصف الأخير من المصفوفة الغوسية
![]()
، يكون
![]()
و
![]()
أي رقمين، فهذا هو SCD (تم تحديد توافق النظام). ولذلك، فإن النظام لديه حل فريد من نوعه .
الغالبية العظمى من الأنظمة هي SCD.
مثال:
على سبيل المثال لدينا هذا النظام:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bab5d5823e45833aa691a3510a2a23eb_l3.png)
الذي المصفوفة الموسعة هي:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}} \ \longrightarrow \ \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f8daea11edeedfd6b86bb251fe19032_l3.png)
لحل النظام نحتاج إلى العمل على صفوف المصفوفة وتحويل جميع العناصر الموجودة أسفل القطر الرئيسي إلى 0. لذلك من الصف الثاني نطرح الصف الأول ومن الصف الثالث نطرح السطر الأول مضروبًا في 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3 -2f_1} & \end{array} \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d68ac25745ddc71d1e7f55f68dd4ea7a_l3.png)
بمجرد أن تصبح جميع الأرقام الموجودة أسفل القطر الرئيسي 0، نعود لتمرير النظام إلى صيغة المعادلة:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 6y+2z=0\\[2ex] 1z=-3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4457f1b034e72c6945bfe609eff52b9a_l3.png)
إذن هذا النظام هو SCD ، حيث يتم إزاحة المصفوفة والصف الأخير من النوع
![]()
. لذلك، نقوم بحلها كما هو الحال دائمًا: عن طريق حذف المجهولات من المعادلات من الأسفل إلى الأعلى.
![]()
![]()
![]()
الآن بعد أن عرفنا z، نعوض بقيمته في المعادلة الثانية لإيجاد قيمة
![]()
:
![]()
![]()
![]()
![]()
![]()
وأخيرًا، نفعل الشيء نفسه مع المعادلة الأولى: نعوض بقيم المجهولات الأخرى ونحل من أجلها
![]()
:
![]()
![]()
![]()
![]()
![]()
![]()
وبالتالي فإن حل نظام المعادلات هو:
![]()
الأنظمة غير المتوافقة بطريقة غاوس
عندما يكون لدينا في مصفوفة غاوس صف به ثلاثة أصفار متتالية ورقم
![]()
، إنه IS (نظام غير متوافق)، وبالتالي، ليس لدى النظام حل .
مثال:
على سبيل المثال، تخيل أنه بعد العمل مع المصفوفة الغوسية للنظام، يتبقى لدينا:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & 1 & -1 & 0 \\[2ex] 0 & 3 & 1 & -1 \\[2ex] 0 & 0 & 0 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-defe65fa616eff800314ebc6dc6f552b_l3.png)
كما هو السطر الأخير
![]()
، أي ثلاثة أصفار متبوعة برقم في النهاية، هي IF (نظام غير متوافق)، وبالتالي، ليس لدى النظام حل .
وعلى الرغم من أنه ليس من الضروري معرفة ذلك، إلا أنك أدناه سترى سبب عدم وجود حل له.
ولو أخذنا السطر الأخير لحصلنا على هذه المعادلة:
![]()
لن تتحقق هذه المعادلة أبدًا، لأنه مهما كانت القيمة z ، فإن ضربها في 0 لن يعطي أبدًا 2 (أي رقم مضروب في 0 يعطي دائمًا 0). وبما أن هذه المعادلة لن تتحقق أبدًا، فليس لدى النظام حل.
الأنظمة المتوافقة غير محددة بالطريقة الغوسية
كلما امتلأ صف من المصفوفة الغوسية بـ 0
![]()
إنه SCI (نظام متوافق غير محدد)، وبالتالي فإن النظام لديه حلول لا حصر لها .
دعونا نرى مثالاً لكيفية حل ICS:
مثال:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-18a63dfebc1f23923714e475aad2e808_l3.png)
كما هو الحال دائمًا، نقوم أولاً بإنشاء المصفوفة الموسعة للنظام :
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\} \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f273040101827fdfea5c9a4858be5567_l3.png)
الآن نريد أن تكون جميع الأرقام الموجودة أسفل القطر الرئيسي 0. لذلك، نضيف إلى الصف الثاني الصف الأول مضروبًا في -2:
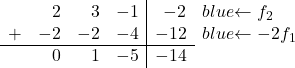
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c889a6f147c6b0430731aa778121af52_l3.png)
لتحويل 3 إلى 0، في السطر الثالث نضيف السطر الأول مضروبًا في -3:
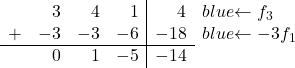
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -3f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c5acccc51108267fef6d3320068743aa_l3.png)
لتحويل 1 في السطر الأخير إلى 0، في السطر الثالث نضيف السطر الثاني مضروبًا في -1:

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a02e4819adfbe7b80d2952f87f113757_l3.png)
بما أن السطر الأخير هو 0 ، فيمكننا إزالته:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6aea469dceab08e6aa62571922eb2824_l3.png)
وبما أن لدينا صفًا كاملاً مليئًا بالصفر، فهذا هو اصابات النخاع الشوكي.
وبذلك ننتهي إلى النظام التالي:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y+2z=6 \\[2ex] y-5z=-14 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-598c031f4cba5a865952a57ed46f0f95_l3.png)
عندما يكون النظام عبارة عن SCI، فمن الضروري أخذ قيمة المعلمة من مجهول
![]()
. ونحن بحاجة إلى حل النظام بناءً على هذه المعلمة
![]()
.
لذلك نحدد قيمة
![]()
إلى ض :
![]()
على الرغم من أنه كان بإمكاننا أيضًا اختيار أي شيء آخر غير معروف لأخذ قيمته
![]()
.
الآن نعزل y عن المعادلة الثانية ونجعلها دالة لـ
![]()
:
![]()
![]()
![]()
وأخيرًا نحذف x من المعادلة الأولى ونتركها أيضًا دالة لـ
![]()
:
![]()
![]()
![]()
![]()
وبالتالي فإن حلول النظام هي:
![]()
كما ترون، عندما يكون النظام هو SCI نترك الحلول حسب المعلمة
![]()
. وتذكر أن لها حلولاً لا حصر لها، لأنها تعتمد على القيمة التي تأخذها
![]()
، الحل سيكون واحدا أو آخر.
قبل الانتقال إلى التمارين التي تم حلها، يجب أن تعلم أنه على الرغم من أننا نستخدم في هذه المقالة طريقة غاوس، إلا أن هناك طريقة أخرى لمناقشة أنظمة المعادلات الخطية وحلها وهي نظرية روش . في الواقع، ربما يتم استخدامه أكثر.
حل تمارين مناقشة أنظمة المعادلات باستخدام طريقة غاوس-جوردان
التمرين 1
حدد نوع النظام المتضمن وحل نظام المعادلات التالي باستخدام طريقة غاوس:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-be4ba1bd1ce7452e66c5189d995d948c_l3.png)
أول شيء يتعين علينا القيام به هو المصفوفة الموسعة للنظام:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex] 3 & 3 & 6 & 9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b600f3fc0d79a06eb972dbacb673a780_l3.png)
الآن نحن بحاجة إلى جعل جميع الأرقام الموجودة أسفل المصفوفة الرئيسية 0.
ولذلك نقوم بإجراء عمليات صفية لإلغاء الحدين الأخيرين من العمود الأول:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex]3 & 3 & 6 & 9 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 2f_1} \\[2ex] \xrightarrow{f_3 - 3f_1}& \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & 1 & -4 \\[2ex] 0 & 0 & 0 & -9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a1d832d5bb115666614ae96822c360eb_l3.png)
لقد حصلنا على صف من المصفوفة يتكون من ثلاثة أصفار متبوعة برقم. ولذلك فهو IS (نظام غير متوافق) وليس هناك حل للنظام.
تمرين 2
حدد نوع النظام وأوجد حل نظام المعادلات التالي باستخدام طريقة غاوس:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7f5aba495f2c6a301e923ee3c6238012_l3.png)
أول شيء يتعين علينا القيام به هو المصفوفة الموسعة للنظام:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8bb5e5ab85946bddad72067fe17d937_l3.png)
الآن نحن بحاجة إلى جعل جميع الأرقام الموجودة أسفل المصفوفة الرئيسية 0.
ولذلك نقوم بإجراء عمليات صفية لإلغاء الحدين الأخيرين من العمود الأول:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 2f_1} \\[2ex] \xrightarrow{f_3 + f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-83e48becaaa6683719ac57eb7d118943_l3.png)
الآن دعونا نحاول إزالة العنصر الأخير من العمود الثاني:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-16a1afc0eb224ee5f05c9e313586854d_l3.png)
لكننا حصلنا على صف كامل من 0s. إذن هذا هو اصابات النخاع الشوكي والنظام لديه عدد لا نهائي من الحلول.
ولكن نظرًا لأنه ICS، فيمكننا حل النظام بناءً عليه
![]()
. لذلك نحذف السطر 0:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-5c838c5f1b229d4c8a43ac9ddd8e3629_l3.png)
نعبر الآن عن المصفوفة في شكل نظام من المعادلات ذات المجهول:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-2y+3z=1 \\[2ex] 1y+5z=7 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b3fd941d33fec646d16b8181430c9986_l3.png)
نعطي قيمة
![]()
ل
![]()
![]()
نستبدل قيمة
![]()
في المعادلة الثانية لإيجاد قيمة
![]()
![]()
![]()
![]()
ونفعل الشيء نفسه مع المعادلة الأولى: نعوض بقيم المجهولات الأخرى ونمحوها
![]()
![]()
![]()
![]()
![]()
وبالتالي فإن حل نظام المعادلات هو:
![]()
التمرين 3
ابحث عن نوع النظام وحل نظام المعادلات التالي بطريقة غاوس:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b04370b42854e53c650ca0eae14aadb5_l3.png)
أول شيء يتعين علينا القيام به هو المصفوفة الموسعة للنظام:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff2c7644e19fdf405f3c5c42ffc0ee98_l3.png)
لتطبيق طريقة غاوس، يكون الأمر أبسط إذا كان الرقم الأول في السطر الأول هو 1. لذلك سنقوم بتغيير ترتيب السطرين 1 و 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 \rightarrow f_2} \\[2ex] \xrightarrow{f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-471d89605d4bf6ddef1896a8fbe4c5ea_l3.png)
الآن نحن بحاجة إلى جعل جميع الأرقام الموجودة أسفل المصفوفة الرئيسية 0.
ولذلك نقوم بإجراء عمليات صفية لإلغاء الحدين الأخيرين من العمود الأول:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 4f_1} \\[2ex] \xrightarrow{f_3 -f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f4d5cbc50b87927077018175c4678e90_l3.png)
نقوم الآن بتحويل العنصر الأخير في العمود الثاني إلى صفر:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{8f_3 + f_2} \end{array} \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-9013720883fd719e2bd0779bfbaa7a9f_l3.png)
هذا النظام هو SCD ، حيث تمكنا من تحويل المصفوفة والصف الأخير من النوع
![]()
. ولذلك، سيكون لها حل فريد من نوعه.
بمجرد أن تصبح جميع الأرقام الموجودة أسفل القطر الرئيسي 0، يمكننا الآن حل نظام المعادلات. للقيام بذلك، نعبر عن المصفوفة مرة أخرى في شكل نظام من المعادلات ذات المجهول:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+1z=2 \\[2ex] -16y-3z=-12 \\[2ex] 5z=20 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0f0433738d5d0a22bdd3b04dbd44fd1e_l3.png)
ونحل مجاهيل المعادلات من الأسفل إلى الأعلى. نقوم أولاً بحل المعادلة الأخيرة:
![]()
![]()
الآن نعوض بقيمة z في المعادلة الثانية لإيجاد قيمة y:
![]()
![]()
![]()
![]()
![]()
ونفعل الشيء نفسه مع المعادلة الأولى: نعوض بقيم المجهولات الأخرى ونحل لـ x:
![]()
![]()
![]()
![]()
وبالتالي فإن حل نظام المعادلات هو:
![]()
التمرين 4
حدد نوع النظام وحل نظام المعادلات التالي بطريقة غاوس:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e8a133547b4719d7833a792550fd322_l3.png)
أول شيء يتعين علينا القيام به هو المصفوفة الموسعة للنظام:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-cc41f78456a922a0fbff419d336b0b46_l3.png)
الآن نحن بحاجة إلى جعل جميع الأرقام الموجودة أسفل المصفوفة الرئيسية 0.
ولذلك نقوم بإجراء عمليات صفية لإلغاء الحدين الأخيرين من العمود الأول:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 3f_1} \\[2ex] \xrightarrow{f_3 + 2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff92912f653c6aca7ceb7c990c9635a3_l3.png)
الآن دعونا نحاول إزالة العنصر الأخير من العمود الثاني:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c6904a64a721f3a92bef8c6b7d713cf_l3.png)
لكننا حصلنا على صف كامل من 0s. إذن هذا هو اصابات النخاع الشوكي والنظام لديه عدد لا نهائي من الحلول.
ولكن نظرًا لأنه ICS، فيمكننا حل النظام بناءً عليه
![]()
. لذلك نحذف السطر 0:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6d856e2c1246f3629d68a7bcd3cd759a_l3.png)
نعبر الآن عن المصفوفة في شكل نظام من المعادلات ذات المجهول:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-1y+4z=2 \\[2ex] -6y+15z=13 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4cf1265bfc12f94580de183230c8b7c_l3.png)
نعطي قيمة
![]()
ل
![]()
![]()
نستبدل قيمة
![]()
في المعادلة الثانية لإيجاد قيمة
![]()
![]()
![]()
![]()
![]()
ونفعل الشيء نفسه مع المعادلة الأولى: نعوض بقيم المجهولات الأخرى ونمحوها
![]()
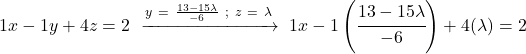
![]()
![]()
لدينا مجموع مع الكسور. لذلك، فإننا نختصر جميع المصطلحات إلى قاسم مشترك:
![]()
![]()
وبما أن جميعها الآن لها نفس المقام، فيمكننا تجميعها في كسر واحد:
![]()
وأخيرًا نتعامل مع البسط:
![]()
![]()
وبالتالي فإن حل نظام المعادلات هو:
![]()