المعادلة المتجهة للمستوى

ستجد في هذه الصفحة معادلة (صيغة) متجه المستوى وأمثلة حسابية. بالإضافة إلى ذلك، ستكون قادرًا على التدرب على التمارين وحل المسائل الخاصة بالمعادلة المتجهة للمستوى.

ما هي المعادلة المتجهات للطائرة؟

في الهندسة التحليلية، المعادلة المتجهة للمستوى هي معادلة تسمح بالتعبير عن أي مستوى رياضيًا. لإيجاد المعادلة المتجهة للمستوى، نحتاج فقط إلى نقطة ومتجهين مستقلين خطيًا ينتميان إلى ذلك المستوى.

صيغة المعادلة المتجهات للطائرة

خذ بعين الاعتبار النقطة ومتجهي الاتجاه للمستوى:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

صيغة المعادلة المتجهة للمستوى هي:

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

ذهب

$\lambda$

$\mu$

هما عددان قياسيان، أي عددان حقيقيان.

لذلك، هذا يعني أنه يمكن التعبير عن أي نقطة في المستوى كمجموعة خطية من نقطة واحدة ومتجهين.

علاوة على ذلك، فإن الشرط الضروري لكي تتوافق المعادلة السابقة مع المستوى هو أن يكون لمتجهي المستوى استقلال خطي، أي أن المتجهين لا يمكن أن يكونا متوازيين مع بعضهما البعض. آخر.

من ناحية أخرى، ضع في اعتبارك أنه بصرف النظر عن المعادلة المتجهة، هناك طرق أخرى للتعبير عن المستوى تحليليًا، مثل المعادلة البارامترية للمستوى والمعادلة الضمنية للمستوى . يمكنك التحقق من كل نوع من المعادلات الموجودة في الروابط.

مثال لكيفية إيجاد المعادلة المتجهة للمستوى

بعد أن رأينا شرح مفهوم المعادلة المتجهة للمستوى، لنرى كيف يتم حسابها من خلال مثال:

أوجد المعادلة المتجهية للمستوى الذي يمر بالنقطة
$P(2,0,4)$

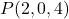
ويحتوي على المتجهات

$\vv{\text{u}}=(1,3,-2)$

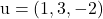
و

$\vv{\text{v}}=(5,0,1).$

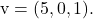
لتحديد المعادلة المتجهة للمستوى، ما عليك سوى تطبيق صيغتها:

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

والآن نعوض بالنقطة وكل متجه في المعادلة:

$\bm{(x,y,z)=(2,0,4)+\lambda (1,3,-2) + \mu (5,0,1)}$

كما ترون في المثال، فإن إيجاد المعادلة المتجهة للمستوى أمر سهل نسبيًا. ومع ذلك، يمكن أن تصبح المسائل معقدة بعض الشيء، لذا ستجد أدناه العديد من التمارين التي تم حلها بصعوبة مختلفة حتى تتمكن من التدرب عليها.

معادلة المتجهات الطائرة تم حل المسائل

التمرين 1

حدد معادلة المتجه للمستوى الذي يحتوي على المتجه

$\vv{\text{u}}=(0,-2,3)$

ويمر عبر النقطتين التاليتين:

$A(1,3,-1)$

$B(2,-1,5).$

انظر الحل

لمعرفة معادلة المستوى، تحتاج إلى نقطة ومتجهين، وفي هذه الحالة لدينا متجه واحد فقط، لذا يجب علينا إيجاد متجه آخر موجه للمستوى. للقيام بذلك، يمكننا حساب المتجه الذي يحدد نقطتي المستوى:

$\vv{AB} = B - A = (2,-1,5) - (1,3,-1) = (1,-4,6)$

الآن بعد أن عرفنا بالفعل متجهي اتجاه للمستوى ونقطة، فإننا نستخدم صيغة معادلة المتجهات للمستوى:

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

ونعوض بالمتجهين وإحدى النقطتين على المستوى في المعادلة:

$\bm{(x,y,z)=(1,3,-1)+\lambda (0,-2,3) + \mu (1,-4,6)}$

تمرين 2

أوجد المعادلة المتجهة للمستوى الذي يحتوي على النقاط الثلاث التالية:

$A(2,-2,1) \qquad B(1,0,4) \qquad C(-1,3,-2)$

انظر الحل

لإيجاد المعادلة المتجهة للمستوى، علينا إيجاد متجهين مستقلين خطيًا يرتبطان في المستوى. ولهذا يمكننا حساب متجهين محددين بالنقاط الثلاث:

$\vv{AB} = B - A = (1,0,4) - (2,-2,1) = (-1,2,3)$

$\vv{AC} = C - A = (-1,3,-2) - (2,-2,1) = (-3,5,-3)$

إحداثيات المتجهين الموجودين غير متناسبة، لذا فهما مستقلان خطيًا عن بعضهما البعض.

الآن بعد أن عرفنا بالفعل متجهي اتجاه ونقطة من المستوى، فإننا نطبق صيغة معادلة المتجهات للمستوى:

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

ونعوض بالمتجهين وإحدى نقاط المستوى الثلاث في المعادلة:

$\bm{(x,y,z)=(2,-2,1)+\lambda (-1,2,3) + \mu (-3,5,-3)}$

التمرين 3

احسب 4 نقاط في الفضاء تنتمي إلى المستوى المحدد بالمعادلة المتجهة التالية:

$(x,y,z)=(0,2,1)+\lambda (2,-1,4) + \mu (-1,3,0)$

انظر الحل

لحساب نقطة على المستوى، ما عليك سوى إعطاء أي قيمة للمعاملات

$\lambda$

$\mu .$

حتى الآن:

$\left. \begin{array}{c} \lambda =0 \\[2ex] \mu =0 \end{array} \right\} \longrightarrow \ (0,2,1)+0\cdot (2,-1,4) + 0\cdot (-1,3,0)= \bm{(0,2,1)}$

$\left. \begin{array}{c} \lambda =1 \\[2ex] \mu =0 \end{array} \right\} \longrightarrow \ (0,2,1)+1\cdot (2,-1,4) + 0\cdot (-1,3,0)= \bm{(2,1,5)}$

$\left. \begin{array}{c} \lambda =0 \\[2ex] \mu =1 \end{array} \right\} \longrightarrow \ (0,2,1)+0\cdot (2,-1,4) + 1\cdot (-1,3,0)= \bm{(-1,5,1)}$

$\left. \begin{array}{c} \lambda =1 \\[2ex] \mu =1 \end{array} \right\} \longrightarrow \ (0,2,1)+1\cdot (2,-1,4) + 1\cdot (-1,3,0)= \bm{(1,4,5)}$

التمرين 4

أوجد المعادلة المتجهة للمستوى الذي يحتوي على الخط

$r$

ويكون موازيا لليمين

$s.$

كونها الخطوط:

$\displaystyle r: \ \begin{cases} x=4+2t \\[1.7ex] y=-1+t\\[1.7ex] z=5-4t \end{cases} \qquad \qquad s: \ \frac{x-1}{2} = \frac{y+2}{4}= \frac{z+1}{-3}$